
(二)、新课讲解
函数的奇偶性定义:
1.偶函数
一般地,对于函数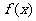 的定义域内的任意一个
的定义域内的任意一个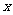 ,都有
,都有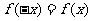 ,那么
,那么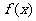 就叫做偶函数.(学生活动)依照偶函数的定义给出奇函数的定义.
就叫做偶函数.(学生活动)依照偶函数的定义给出奇函数的定义.
2.奇函数
一般地,对于函数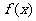 的定义域的任意一个
的定义域的任意一个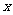 ,都有
,都有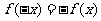 ,那么
,那么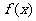 就叫做奇函数.
就叫做奇函数.
注意:
①函数是奇函数或是偶函数称为函数的奇偶性,函数的奇偶性是函数的整体性质;
②由函数的奇偶性定义可知,函数具有奇偶性的一个必要条件是,对于定义域内的任意一个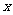 ,则
,则 也一定是定义域内的一个自变量(即定义域关于原点对称).
也一定是定义域内的一个自变量(即定义域关于原点对称).
3.具有奇偶性的函数的图象的特征
偶函数的图象关于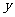 轴对称;奇函数的图象关于原点对称.
轴对称;奇函数的图象关于原点对称.
例1.判断下列函数是否是偶函数.
(1)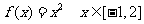
(2)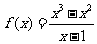
解:函数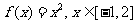 不是偶函数,因为它的定义域关于原点不对称.
不是偶函数,因为它的定义域关于原点不对称.
函数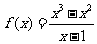 也不是偶函数,因为它的定义域为
也不是偶函数,因为它的定义域为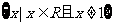 ,并不关于原点对称
,并不关于原点对称
例2.判断下列函数的奇偶性
(1)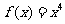 (2)
(2)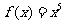 (3)
(3)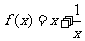 (4)
(4)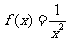
解:(略)
归纳:利用定义判断函数奇偶性的格式步骤:
①首先确定函数的定义域,并判断其定义域是否关于原点对称;
②确定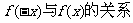 ;
;
③作出相应结论:
若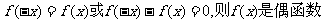 ;
;
若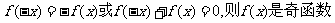 .
.
例3.判断下列函数的奇偶性:
①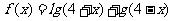
②
分析:先验证函数定义域的对称性,再考察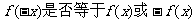 .
.
解:(1)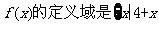 >0且
>0且 >
>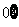 =
=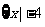 <
<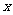 <
< ,它具有对称性.因为
,它具有对称性.因为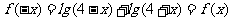 ,所以
,所以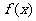 是偶函数,不是奇函数.
是偶函数,不是奇函数.
(2)当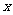 >0时,-
>0时,-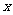 <0,于是
<0,于是
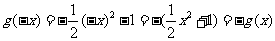
当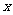 <0时,-
<0时,-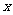 >0,于是
>0,于是
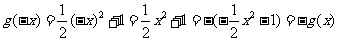
综上可知,在R∪R+上,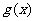 是奇函数.
是奇函数.
例4.已知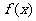 是奇函数,在(0,+∞)上是增函数.
是奇函数,在(0,+∞)上是增函数.
证明: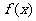 在(-∞,0)上也是增函数.
在(-∞,0)上也是增函数.
证明:(略)
归纳:偶函数在关于原点对称的区间上单调性相反;奇函数在关于原点对称的区间上单调性一致.
巩固深化
(1)课本P40 练习1.2
(2)判断下列函数的奇偶性,并说明理由.
①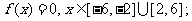
②
③
④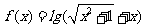
(一)、复习提问:
“对称”是大自然的一种美,这种“对称美”在数学中也有大量的反映,让我们看看下列各函数有什么共性?
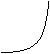
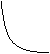
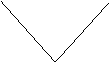
观察下列函数的图象,总结各函数之间的共性.
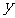
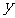
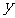

|
|



|
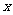 -1
-1
 0
0
|
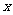
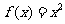
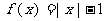
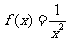
通过讨论归纳:函数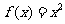 是定义域为全体实数的抛物线;函数
是定义域为全体实数的抛物线;函数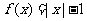 是定义域为全体实数的折线;函数
是定义域为全体实数的折线;函数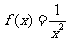 是定义域为非零实数的两支曲线,各函数之间的共性为图象关于
是定义域为非零实数的两支曲线,各函数之间的共性为图象关于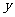 轴对称.观察一对关于
轴对称.观察一对关于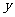 轴对称的点的坐标有什么关系?
轴对称的点的坐标有什么关系?
归纳:若点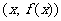 在函数图象上,则相应的点
在函数图象上,则相应的点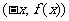 也在函数图象上,即函数图象上横坐标互为相反数的点,它们的纵坐标一定相等.
也在函数图象上,即函数图象上横坐标互为相反数的点,它们的纵坐标一定相等.
重点:函数的奇偶性及其几何意义
难点:判断函数的奇偶性的方法与格式
2. 学会运用函数的图象理解和研究函数的性质,体会数形结合的数学方法.
1. 结合熟悉的具体函数,了解奇偶性和周期性的含义,通过具体函数的图象,初步了解中心对称图形和轴对称图形。
(四)作业
1.求函数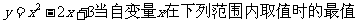 .
.
①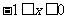 ②
② 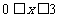 ③
③
(三)小结
本节课主要学习了求函数最值的常用方法,目前主要有:
(1)配方法:即将函数解析式化成含有自变量的平方式与常数的和,然后根据变量的取值范围确定函数的最值.
(2)换元法:通过变量式代换转化为求二次函数在某区间上的最值.
(3)数形结合法:利用函数图象或几何方法求出最值.
(二)、新课讲解
1.函数最大(小)值定义
最大值:一般地,设函数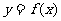 的定义域为I,如果存在实数M满足:
的定义域为I,如果存在实数M满足:
(1)对于任意的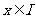 ,都有
,都有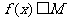 ;
;
(2)存在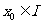 ,使得
,使得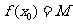 .
.
那么,称M是函数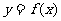 的最大值.
的最大值.
思考:依照函数最大值的定义,结出函数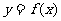 的最小值的定义.
的最小值的定义.
注意:
①函数最大(小)首先应该是某一个函数值,即存在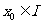 ,使得
,使得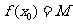 ;
;
②函数最大(小)应该是所有函数值中最大(小)的,即对于任意的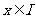 ,都有
,都有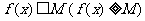 .
.
2.几种判断函数最大(小)值的简单方法.
①配方法 ②换元法 ③数形结合法
例1.(教材P34例3)利用二次函数的性质确定函数的最大(小)值.
解(略)
例2.将进货单价40元的商品按50元一个售出时,能卖出500个,若此商品每个涨价1元,其销售量减少10个,为了赚到最大利润,售价应定为多少?
解:设利润为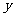 元,每个售价为
元,每个售价为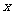 元,则每个涨(
元,则每个涨(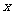 -50)元,从而销售量减少
-50)元,从而销售量减少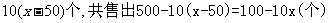
∴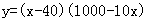
 <100)
<100)
∴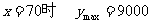
答:为了赚取最大利润,售价应定为70元.
例3.求函数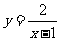 在区间[2,6] 上的最大值和最小值.
在区间[2,6] 上的最大值和最小值.
解:(略)
例4.求函数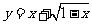 的最大值.
的最大值.
解:令
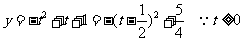
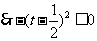
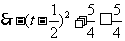

巩固深化
(1)P36练习4
(2)求函数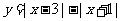 的最大值和最小值.
的最大值和最小值.
 (3)如图,把截面半径为25cm的图形木头锯成矩形木料,如果矩形一边长为
(3)如图,把截面半径为25cm的图形木头锯成矩形木料,如果矩形一边长为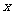 ,面积为
,面积为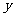 ,试将
,试将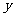 表示成
表示成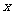 的函数,并画出函数的大致图象,并判断怎样锯才能使得截面面积最大?
的函数,并画出函数的大致图象,并判断怎样锯才能使得截面面积最大?

(一)、复习提问:学生动手画出下列函数的图象,指出图象的最高点或最低点,并说明它能体现函数的什么特征?
①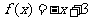 ②
②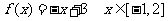
③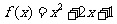 ④
④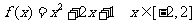
函数的最大(小)值及其几何意义
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com