1° 看电影时，电影票与座位之间存在者一一对应的关系。

2° 对任意实数a，数轴上都有唯一的一点A与此相对应。

3° 坐标平面内任意一点A 都有唯一的有序数对(x, y)和它对应。

4° 任意一个三角形，都有唯一的确定的面积与此相对应。

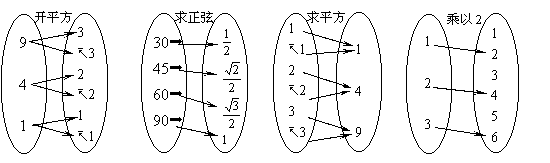
　　 (1)　　　 　　　(2)　　　　　　 (3)　　　　　　 (4)

引导观察，分析以上三个实例。注意讲清以下几点：

1．先讲清对应法则：然后，根据法则，对于集合A中的每一个元素，在集合B中都有一个(或几个)元素与此相对应。

2．求双曲线的标准方程：

(1)实轴的长是10，虚轴长是8，焦点在x轴上；

(2)焦距是10，虚轴长是8，焦点在y轴上；

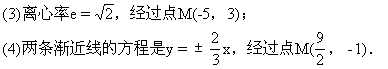
曲线的方程．

点到两准线及右焦点的距离．

作业答案：

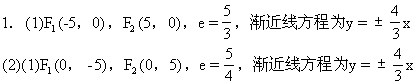
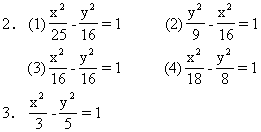
距离为7

1．已知双曲线方程如下，求它们的两个焦点、离心率e和渐近线方程．

(1)16x2-9y2=144；

(2)16x2-9y2=-144．

(七)小结(由学生课后完成)

将双曲线的几何性质按两种标准方程形式列表小结．

(六)双曲线的第二定义

1．定义(由学生归纳给出)

平面内点M与一定点的距离和它到一条直线的距离的比是常数e=

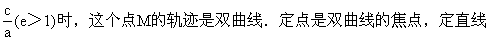
叫做双曲线的准线，常数e是双曲线的离心率．

2．说明

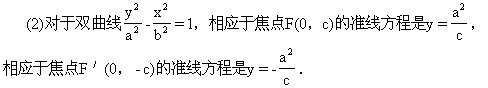
(五)练习与例题

1．求双曲线9y2-16x2=144的实半轴长和虚半轴长、焦点坐标、离心率、渐近线方程．

请一学生演板，其他同学练习，教师巡视，练习毕予以订正．

由此可知，实半轴长a=4，虚半轴长b=3．

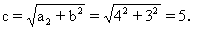
焦点坐标是(0，-5)，(0，5)．

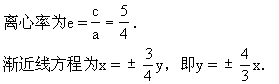
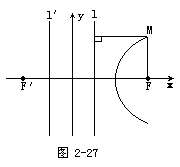
本题实质上是双曲线的第二定义，要重点讲解并加以归纳小结．

解：设d是点M到直线l的距离，根据题意，所求轨迹就是集合：

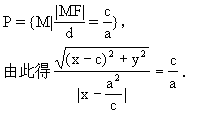
化简得：(c2-a2)x2-a2y2=a2(c2-a2)．

这就是双曲线的标准方程．

由此例不难归纳出双曲线的第二定义．

(四)顺其自然介绍离心率(性质5)

由于正确认识了渐近线的概念，对于离心率的直观意义也就容易掌握了，为此，介绍一下双曲线的离心率以及它对双曲线的形状的影响：

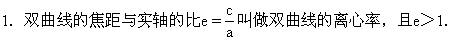
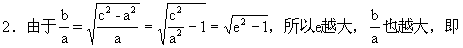
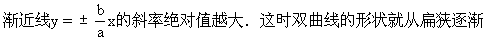
变得开阔，从而得出：双曲线的离心率越大，它的开口就越开阔．

这时，教师指出：焦点在y轴上的双曲线的几何性质可以类似得出，双曲线的几何性质与坐标系的选择无关，即不随坐标系的改变而改变．

(三)问题之中导出渐近线(性质4)

在学习椭圆时，以原点为中心，2a、2b为邻边的矩形，对于估计

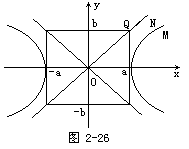
仍以原点为中心，2a、2b为邻边作一矩形(板书图形)，那么双曲线和这个矩形有什么关系？这个矩形对于估计和画出双曲线简图(图2-26)有什么指导意义？这些问题不要求学生回答，只引起学生类比联想．

接着再提出问题：当a、b为已知时，这个矩形的两条对角线的方程是什么？

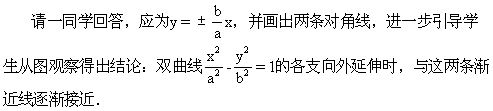
下面，我们来证明它：

双曲线在第一象限的部分可写成：

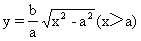
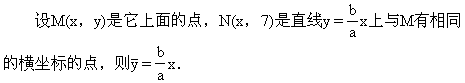
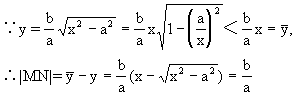
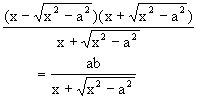
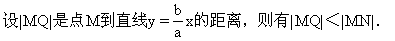
当x逐渐增大时，|MN|逐渐减小，x无限增大，|MN|接近于零，|MQ|也接近于零，就是说，双曲线在第一象限的部分从射线ON的下方逐渐接近于射线ON．

在其他象限内也可以证明类似的情况．

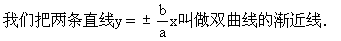
现在来看看实轴在y轴上的双曲线的渐近线方程是怎样的？由于焦点在y轴上的双曲线方程是由焦点在x轴上的双曲线方程，将x、y字

母对调所得到，自然前者渐近线方程也可由后者渐近线方程将x、y字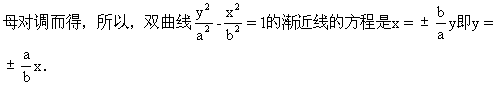

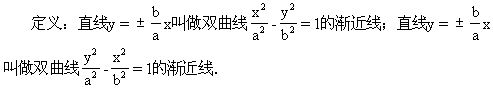
这样，我们就完满地解决了画双曲线远处趋向问题，从而可比较精

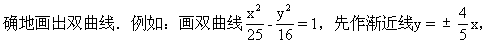
再描几个点，就可以随后画出比较精确的双曲线．

(二)类比联想得出性质(性质1-3)

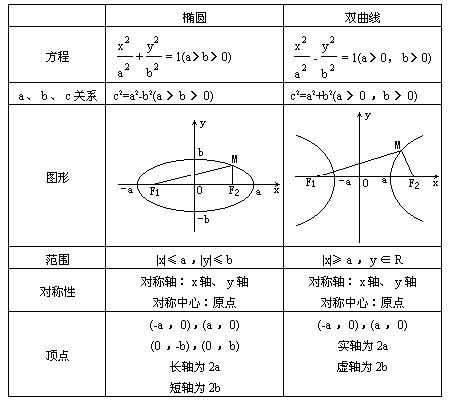
引导学生完成下列关于椭圆与双曲线性质的表格(让学生回答，教师引导、启发、订正并板书)．<见下页>

(一)复习提问引入新课

1．椭圆有哪些几何性质，是如何探讨的？

请一同学回答．应为：范围、对称性、顶点、离心率，是从标准方程探讨的．

2．双曲线的两种标准方程是什么？

再请一同学回答．应为：中心在原点、焦点在x轴上的双曲线的标

下面我们类比椭圆的几何性质来研究它的几何性质．