
16.(本小题满分13分)
解:(Ⅰ) ……2分
……2分
 …………3分
…………3分
 ;
…………………………4分
;
…………………………4分
由 ,
,  ………………6分
………………6分
 ……………………7分
……………………7分
(Ⅱ)  ,
,
 ;
…………………8分
;
…………………8分
所以 ……………9分
……………9分
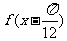 =
= …………………10分
…………………10分
(Ⅲ)由题意知 ,所以
,所以 ; ………………12分
; ………………12分
 ,故
,故 为奇函数. …………13分
为奇函数. …………13分
(二)选做题(14-15题,考生只能从中选做一题)
14.
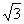 .解析:由题意知,直线
.解析:由题意知,直线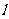 的倾斜角为
的倾斜角为 ,并过点
,并过点 (2,0);曲线
(2,0);曲线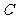 是以(1,0)为圆心、半径为1的圆,且圆
是以(1,0)为圆心、半径为1的圆,且圆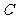 也过点
也过点 (2,0);设直线
(2,0);设直线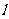 与圆
与圆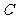 的另一个交点为
的另一个交点为 ,在
,在 中,
中, .
.
15. ,
,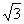 .解析:由切割线定理得
.解析:由切割线定理得 ,
,
 ;连结OC,则
;连结OC,则 ,
, ,
,
 .
.
10.A.解析:设 ,由导数不难知道直线
,由导数不难知道直线 的斜率分别为
的斜率分别为 进一步得
进一步得
 ①
① ②,由①②可得点
②,由①②可得点 ,(1)因为
,(1)因为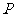 在
在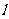 上,所以
上,所以 ,所以
,所以 ,所以
,所以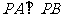 ;(2)若
;(2)若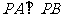 ,
,  ,即
,即 ,从而点
,从而点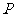 在
在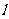 上.
上.
9.A.解析: ,而
,而 表示过点(x,y)与(-1.-1)连线的斜率,易知
表示过点(x,y)与(-1.-1)连线的斜率,易知 ,所以可作出可行域,知
,所以可作出可行域,知 的最小值是
的最小值是 即
即 .
.
涉及到线性规划的题目,每年必考;就此题而言,式子 的处理应当成为解决本题的关键,一般来说,高考题中的分式结构在处理方式上一般是分离变形,这样其几何意义就表现来了.
的处理应当成为解决本题的关键,一般来说,高考题中的分式结构在处理方式上一般是分离变形,这样其几何意义就表现来了.
8.D.解析:易知当且仅当 时两条直线只有一个交点,而
时两条直线只有一个交点,而 的情况有三种:
的情况有三种:
 (此时两直线重合);
(此时两直线重合); (此时两直线平行);
(此时两直线平行); (此时两直线平行).而投掷两次的所有情况有
(此时两直线平行).而投掷两次的所有情况有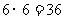 种,所以两条直线相交的概率
种,所以两条直线相交的概率 ;两条直线平行的概率为
;两条直线平行的概率为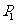 =
= ,
,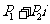 所对应的点为
所对应的点为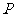
 ,易判断
,易判断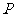
 在
在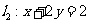 的左下方,选D.
的左下方,选D.
本题 融合了直线、线性规划、概率及复数等有关知识,在处理方法上可采用枚举法处理,注意不等忽视了直线重合这种情况,否则会选C.
7.A.解析:当 时,此时
时,此时 ;当
;当 时,此时
时,此时 ;当
;当 时,此时
时,此时 ;当
;当 时,此时
时,此时 ;当
;当 时,此时
时,此时 ;此时只要p的值为15即可使得判断框取“否”,从而输出n的值为5.
;此时只要p的值为15即可使得判断框取“否”,从而输出n的值为5.
处理此类问题时,一定要注意多写几步,从中观察得出答案;本题若将 与
与 的位置调换一下,则情况又如何呢?同学们可以考虑一下.
的位置调换一下,则情况又如何呢?同学们可以考虑一下.
6.B.解析:由向量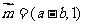 和
和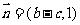 共线知
共线知 ①,由
①,由 ②,由c>b>a知角B为锐角,
②,由c>b>a知角B为锐角, ③,联立①②③得b=2.
③,联立①②③得b=2.
5.C.解析:如图(1),在平面内不可能有符合题意的点;如图(2),直线a、b到已知平面的距离相等且所在平面与已知平面垂直,则已知平面为符合题意的点;如图(3),直线a、b所在平面与已知平面平行,则符合题意的点为一条直线,从而选C.



4.D.解析:由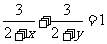 可化为xy
=8+x+y,
可化为xy
=8+x+y, x,y均为正实数,
x,y均为正实数, xy =8+x+y
xy =8+x+y (当且仅当x=y等号成立)即xy-2
(当且仅当x=y等号成立)即xy-2 -8
-8 ,可解得
,可解得
 ,即xy
,即xy 16故xy的最小值为16.
16故xy的最小值为16.
解决本题的关键是先变形,再利用基本不等式 来构造一个新的不等式.
来构造一个新的不等式.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com