
1、连续掷3次硬币,那么互为对立的事件是 ( C )
A、至少一次是正面和最多有一次正面;
B、最多有一次正面和恰有两次正面;
C、不多于一次正面和至少有两次正面;
D、至少有两次正面和恰有一次正面.
3.对立事件:
两个互斥事件必有一个发生,则称这两个事件为对立事件.事件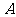 的对立事件记为
的对立事件记为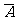 .
.
对立事件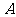 和
和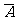 必有一个发生,故
必有一个发生,故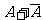 是必然事件,从而
是必然事件,从而
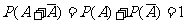 .
.
因此,我们可以得到一个重要公式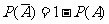 .
.
[精典范例]
例1 一个射手进行一次射击,试判断下列事件哪些是互斥事件?哪些是对立事件?
事件A:命中环数大于7环;
事件B:命中环数为10环;
事件C:命中环数小于6环;
事件D:命中环数为6、7、8、9、10环.
[分析]要判断所给事件是对立还是互斥,首先将两个概念的联系与区别弄清楚,互斥事件是指不可能同时发生的两事件,而对立事件是建立在互斥事件的基础上,两个事件中一个不发生,另一个必发生.
[解]A与C互斥(不可能同时发生),B与C互斥,C与D互斥,C与D是对立事件(至少一个发生).
例2 一只口袋内装有大小一样的4只白球与4只黑球,从中一次任意摸出2只球.记摸出2只白球为事件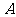 ,摸出1只白球和1只黑球为事件
,摸出1只白球和1只黑球为事件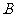 .问事件
.问事件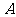 和
和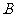 是否为互斥事件?是否为对立事件?
是否为互斥事件?是否为对立事件?
[解] 事件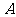 和
和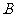 互斥
互斥
因为从中一次可以摸出2只黑球,所以事件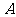 和
和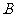 不是对立事件.
不是对立事件.
例3 某人射击1次,命中7---10环的概率如下表所示:
|
命中环数 |
10环 |
9环 |
8环 |
7环 |
|
概率 |
0.12 |
0.18 |
0.28 |
0.32 |
(1) 求射击一次,至少命中7环的概率;
(2) 求射击1次,命中不足7环的概率.
[解] 记事件“射击1次,命中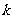 环”为
环”为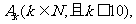 则事件
则事件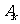 两两相斥.
两两相斥.
(1)记“射击一次,至少命中7环”的事件为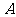 ,那么当
,那么当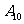 ,
,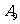 ,
,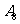 或
或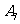 之一发生时,事件
之一发生时,事件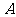 发生.由互斥事件的概率加法公式,得
发生.由互斥事件的概率加法公式,得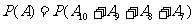
=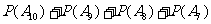
=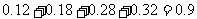 .
.
(2)事件“射击一次,命中不足7环”是事件“射击一次,命中至少7环”的对立事件,即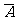 表示事件“射击一次,命中不足7环”.根据对立事件的概率公式,得
表示事件“射击一次,命中不足7环”.根据对立事件的概率公式,得
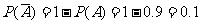 .
.
答 此人射击1次,至少命中7环的概率为0.9;命中不足7环的概率为0.1.
例4 黄种人群中各种血型的人所占的比如下表所示:
|
血型 |
A |
B |
AB |
O |
|
该血型的人所占比/% |
28 |
29 |
8 |
35 |
已知同种血型的人可以输血,O型血可以输给任一种血型的人,任何人的血都可以输给AB型血的人,其他不同血型的人不能互相输血.小明是B型血,若小明因病需要输血,问:
(1)任找一个人,其血可以输给小明的概率是多少?
(2)任找一个人,其血不能输给小明的概率是多少?
[解] (1)对任一人,其血型为A,B,AB,O型血的事件分别记为 它们是互斥的.由已知,有
它们是互斥的.由已知,有
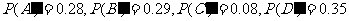 .
.
因为B,O型血可以输给B型血的人,故“可以输给B型血的人”为事件 .根据互斥事件的加法公式,有
.根据互斥事件的加法公式,有
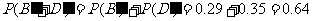 .
.
(2)由于A,AB型血不能输给B型血的人,故“不能输给B型血的人”为事件
 ,且
,且
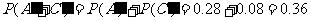 .
.
答 任找一人,其血可以输给小明的概率为0.64,其血不能输给小明的概率为0.36.
注 :第(2)问也可以这样解:因为事件“其血可以输给B型血的人”与事件“其血不能输给B型血的人”是对立事件,故由对立事件的概率公式,有

追踪训练
2.互斥事件的概率 :
如果事件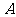 ,
,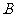 互斥,那么事件
互斥,那么事件 发生的概率,等于事件
发生的概率,等于事件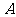 ,
,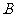 分别发生的概率的和,即
分别发生的概率的和,即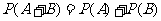 .
.
一般地,如果事件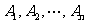 两两互斥,则
两两互斥,则
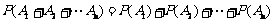 .
.
1.互斥事件:
不能同时发生的两个事件称为互斥事件.
2、正确理解两个互斥事件的概率加法公式,会用相关公式进行简单概率计算.
[课堂互动]
自学评价
案例:体育考试的成绩分为四个等级:优、良、中、不及格,某班50名学生参加了体育考试,结果如下:
|
优 |
85分及以上 |
9人 |
|
良 |
75----84分 |
15人 |
|
中 |
60----74分 |
21人 |
|
不及格 |
60分以下 |
5人 |
问题:在同一次考试中,某一位同学能否既得优又得良?从这个班任意抽取一位同学,那么这位同学的体育成绩为“优良”(优或良)的概率是多少?
[解]体育考试的成绩的等级为优、良、中、不及格的事件分别记为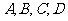 .在同一次体育考试中,同一人不能同时既得优又得良,即事件
.在同一次体育考试中,同一人不能同时既得优又得良,即事件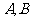 是不可能同时发生的.
是不可能同时发生的.
在上述关于体育考试成绩的问题中,用事件 表示事件“优”和“良”,那么从50人中任意抽取1个人,有50种等可能的方法,而抽到优良的同学的方法有
表示事件“优”和“良”,那么从50人中任意抽取1个人,有50种等可能的方法,而抽到优良的同学的方法有
9+15种,从而事件 发生的概率
发生的概率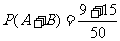 .
.
另一方面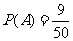 ,
,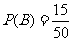 ,因此有
,因此有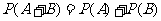 .
.
[小结]
1、了解互斥事件及对立事件的概念,能判断某两个事件是否是互斥事件,进而判断它们是否是对立事件.
7.4.1 互斥事件及其发生的概型
第38课时
学习要求
3、两根相距6m的木杆上系一根绳子,并在绳子上挂一盏灯,求灯与两端距离都大于2m的概率.
解:记“灯与两端距离都大于2m”为事件A,则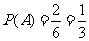 .
.

2、在区间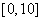 中任意取一个数,则它与2之和大于
中任意取一个数,则它与2之和大于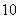 的概率是_____1/5___________
的概率是_____1/5___________
1、如图,有一圆盘其中的阴影部分的圆心角为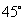 ,若向圆内投镖,如果某人每次都投入圆内,那么他投中阴影部分的概率为 ( A )
,若向圆内投镖,如果某人每次都投入圆内,那么他投中阴影部分的概率为 ( A )
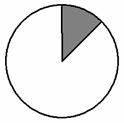
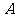 .
.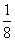
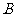 .
.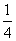
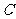 .
.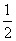
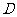 .
.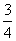
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com