
12.解法一:在同一坐标系中,分别画出两个函数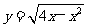 和
和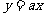 的图象.如下图所示,欲使解区间恰为
的图象.如下图所示,欲使解区间恰为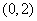 ,则直线
,则直线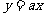 必过点
必过点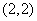 ,则
,则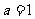 .
.
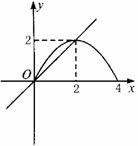
解法二:∵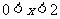 ,当
,当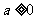 时,则
时,则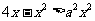 .
.
∴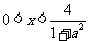 ,则
,则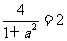 ,∴
,∴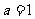 .
.
当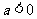 时,原不等式的解为
时,原不等式的解为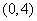 ,与题意不符,
,与题意不符,
∴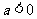 舍去.综上知
舍去.综上知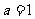 .
.
第32课 函数与方程小结与复习(3)
11.令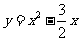 ,
,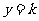 ,则方程有实根等价于直线
,则方程有实根等价于直线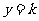 与抛物线
与抛物线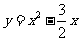 ,
,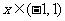 的图象有交点,而函数
的图象有交点,而函数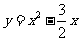 ,
,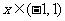 的值域为
的值域为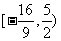 ,∴
,∴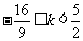 。
。
10.设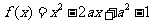 ,依题意得
,依题意得
∴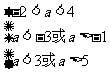 ,∴
,∴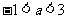 .
.
故当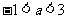 时,原方程的两实根在区间
时,原方程的两实根在区间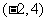 内.
内.
9.设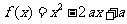 .
.
(1)由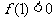 ,解得
,解得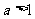 .
.
(2)由题意可知,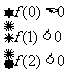
∴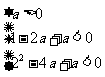 解得
解得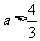 .
.
6.C 7.A 8.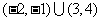
1.D 2.B 3.D 4.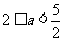 5.
5.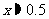
2.(1)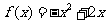 ;
;
(2)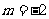 ,
,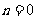 .
.
10. (1) 由已知
解得: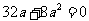 ,
,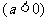 ,
,
∴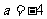 从而
从而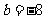 , ∴
, ∴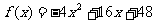 .
.
(2)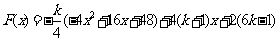

欲使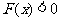 恒成立,则
恒成立,则 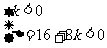
解得 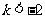 .
.
∴满足条件的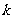 的取值范围是
的取值范围是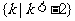 .
.
9.(1)若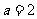 ,
,
当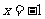 时,
时,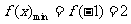 ;
;
当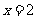 时,
时,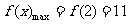 .
.
(2)函数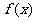 的对称轴为
的对称轴为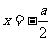 ,
,
①当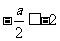 ,即
,即 时,
时,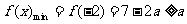 ,
,
得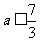 ,无解;
,无解;
②当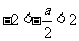 ,即
,即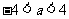 时,
时,
若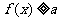 恒成立,则
恒成立,则 ,解得
,解得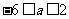
∴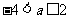 ;
;
③当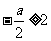 ,即
,即 时,
时,
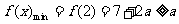 ,
,
得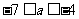 .
.
综合①②③可得 .
.
6.D 7.A 8.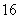
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com