
2.已知集合M={x|x≤-1},N={x|x>a-2},若M∩N≠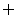 ,则a满足的条件是什么?
,则a满足的条件是什么?
例4:
已知集合A={2,5},B={x|x2+px+q=0,x∈R}
(1)若B={5},求p,q的值.
(2)若A∩B= B ,求实数p,q满足的
条件.
分析:
(1)由B={5},知:方程x2+px+q=0有两个
相等,再用一元二次方程的根与系数的关系容易求p,q的值.
(2)由A∩B= B可知:B 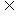 A,而A={2,5}从而顺利地求出实数p,q满足的条件.
A,而A={2,5}从而顺利地求出实数p,q满足的条件.
[解]
(1)∵ A∩B={5}
∴ 方程x2+px+q=0有两个相等的实根5
∴ 5+5=-p 5•5=q
∴ p=-10,q=25
(2)
∵
A∩B= B ∴ B 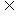 A
A
当B=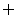 时,⊿=p2-4q<0,即 p2<4q;
时,⊿=p2-4q<0,即 p2<4q;
当B={2}时,可求得p=-4,q=4;
当B={5}时,p=-10,q=25;
当B={2,5}时,可求得p=-7,q=10;
综上所述:
实数p,q满足的条件为p2<4q;
或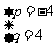 或
或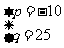
或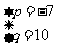
点评:
利用性质:A∩B = A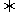 A
A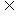 B是解题的
B是解题的
关键,提防掉进空集这一陷阱之中.
追踪训练二
1.已知集合A={x|x2+x-6=0},B={x|mx+1=0
=0},若A∩B =B,求实数m所构成的集合M.
4. 设集合A={x||x=2k+1,k∈Z},B={y|y=2k-1,k∈Z},C={x|x=2k ,k∈Z},
求A∩B,B∩C.
3. 设集合A={(x,y)|y=-4x+6,x∈R},B={(x,y)|x=y2-1}求A∩B;
2. 设集合A={x|x≥0},B={x|x≤0,x∈R},求A∩B;
例1.
(1)设A={-1,0,1},B={0,1,2,3},求A∩B;
(2)设A={x|x>0},B={x|x≤1},求A∩B;
(3)设A={x|x=3k,k∈Z},B={y|y=3k+1 k∈Z },C={z|z=3k+2,k∈Z},D={x|x=6k+1,k∈Z},求A∩B;
A∩C;C∩B;D∩B;
[解]
(1)A∩B={0,1};
(2)A∩B={x|0<x≤1};
(3)A∩B= A∩C= C∩B=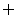
D∩B= D
点评:
不等式的集合求交集时,运用数轴比
较直观,形象.
例2:
已知数集 A={a2,a+1,-3},数集B={a-3,a-2,a2+1},若A∩B={-3},求a的值.
[解]
∵ A∩B={-3}
∴ -3 ∈ A -3 ∈ B
当a-3=-3时,即a= 0时,B={-3,-2,1},
A={0,1,-3}满足题意;
当a-2=-3时,即a=-1时,B={-4,-3,2},
A={1,0,-3}不满足题意;
∴ a = 0
点评:
在集合的运算中,求有关字母的值时,要注意分类讨论及验证集合的特性.
例3:
(1)设集合A={y|y=x2-2x+3,x∈R},
B={y|y=-x2+2x+10,x∈R},
求A∩B;
(2)设集合A={(x,y)|y=x+1,x∈R},
B={(x,y)|y=-x2+2x+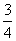 ,x∈R},
,x∈R},
求A∩B;
分析:
先求出两个集合的元素,或者集合中元素
的范围,再进行交集运算.特别注意(1)、
(2)两题的区别,这是同学们容易忽视的地方.
[解]
(1) 两个集合表示的是y的取值范围,
∵A={y|y=x2-2x+3,x∈R}= {y|y≥2},
B={y|y=-x2+2x+10,x∈R}= {y|y≤11},
∴ A∩B={y|2≤y≤11};
(2)A∩B= {(x,y)|y=x+1,x∈R}∩{(x,y)|y=-x2+2x+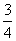 ,x∈R}
,x∈R}
={(x,y)| 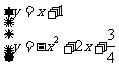 }
}
={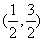 }
}
点评:
求集合的交集时,注意集合的实质,是点集还时数集.是数集求元素的公共部分,是点集的求方程组的解所组成的集合.
追踪训练一
1. 设集合A={小于7的正偶数},B={-2,0,2,4},求A∩B;

4.已知集合A={x|x2-1=0 },B={x|x2-2ax+b=0}
B 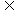 A,求a,b的取值范围.
A,求a,b的取值范围.
思维点拔:
集合中的开放问题
例5: 已知全集S={1,3x3+3x2+2x},集合
A={1,|2x-1|},如果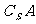 ={0},则这样的
={0},则这样的
实数x是否存在?若存在,求出x,若不
存在,请说明理由.
点拔:
由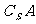 ={0},可知,0∈S,但0
={0},可知,0∈S,但0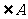 ,由
,由
0∈S,可求出x,然后结合0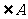 ,来验证
,来验证
是否符合题目的隐含条件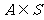 ,从而确定
,从而确定
x是否存在.
|
学生质疑 |
|
|
教师释疑 |
|
[师生互动]
3.已知集合A={x|x=a+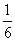 ,a∈Z},B={x|x=
,a∈Z},B={x|x=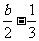 ,b∈Z},C={x|x=
,b∈Z},C={x|x=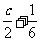 ,c∈Z},试判断A、B、C满足的关系
,c∈Z},试判断A、B、C满足的关系
2.设全集是数集U={2,3,a2+2a-3},已知
A={b,2},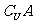 ={5},求实数a,b的值.
={5},求实数a,b的值.
例4:①方程组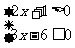 的解集为A,
的解集为A,
U=R,试求A及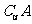 .
.
②设全集U=R,A={x|x>1},B={x|x+a<0},
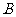 是
是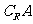 的真子集,求实数a的取值范围.
的真子集,求实数a的取值范围.
[解]
① A={x|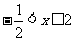 },
},
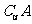 ={x|x≤
={x|x≤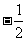 或x>2}
或x>2}
② B={x|x+a<0}={x|x<-a} ,
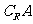 ={x|x≤1}
={x|x≤1}
∵ 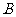 是
是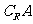 的真子集
的真子集
如图所示:
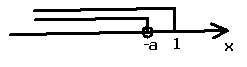 ∴
-a ≤ 1即a≥-1
∴
-a ≤ 1即a≥-1
点评:
求集合的补集时通常借助于数轴,比较形象,直观.
追踪训练二
1.若U=Z,A={x|x=2k,k∈Z},B={x|x=2k+1, k∈Z},则 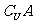 ___________
___________

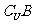 ___________:
___________:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com