
例1:判断下列函数是否是奇函数或偶函数:
判断下列函数的奇偶性:
(1)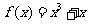 (2)
(2)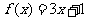
(3)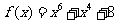 ,
,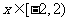
(4)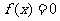 (5)
(5)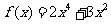
分析:函数的奇偶性的判断和证明主要用定义。
24.解: 由a1<a2<a3<a4
,A∩B={a1,a4},可知 a1=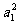 , ∴ a1=1
, ∴ a1=1
∵ a1+a4=10,∴ a4=9 ,
若 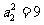 ,a2=3,则有(1+3+ a3 +9)+(
,a2=3,则有(1+3+ a3 +9)+(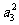 +81)=124
+81)=124
解得a3 =5,(a3 =-6舍去)
∴ A={1,3,5,9},B={1,9,25,81}.
若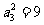 ,a3=3,此时只能有a2=2,
,a3=3,此时只能有a2=2,
则A∪B中所有元素和为:1+2+3+4+9+81≠124,
∴ 不合题意.
于是,A={1,3,5,9},B={1,9,25,81}.
23.略解
(1)-1≤a≤2
(2) a<-1或a>2
22.解: 由A={a},故A中的方程有一个根a,
∴ ⊿=(b+2)2-4(b+1)=0
即 b=0
∴ a=-1
∴ B={x|x2-x=0}={0,1}
从而B的真子集为{0},{1},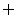
21.解:
∵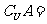 {5},
{5},
∴ 5∈U,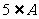
∴ a2+2a-3=5,解得a=2或a=-4
当a=2 时,|2a-1|=3≠5
当a=-4是时,|2a-1|=9 ≠5,但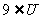 ,
,
∴ a=2
19.20 20.x≤-2
13.C 14.A 15.D 16.C 17.0或1 18.M N
12.解: A={0,-4}
(1) ∵ A∩B=B ∴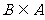
B=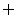 或{0}或{-4}或{0,-4}
或{0}或{-4}或{0,-4}
以下对B的四种情况分别讨论
综合得如下结论: a≤-1,或a=1
(2) ∵
A∪B=B ∴ 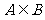
∵ A={0,-4},而B中最多有两个元素,
∴ A =B
即 a=1

11.解: ∵ A∩B={-1,7}
∴ 7∈A,即有x2-x+1=7, 解得: x=-2或x=3
当x=-2时,x+4=2∈B,与2∈A∩B矛盾;
当x=3时,x+4=7,这时2y=-1即y=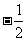
∴ x=3,y=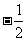
10.略解a=-1或a=0.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com