2．2009年8月，台风“　 ▲ 　”卷过，给海峡两岸造成严重灾情，更重创台湾中南部。大陆各界第一时间伸出援手，掀起捐助高潮，赈灾款项、物资不断涌进台湾。

A．天鹅　　　　　 B．鲸鱼　　　　　 C．莫拉克　　　　 D． 莲花

1．2009年是中华人民共和国成立　 ▲　 周年和“五四”运动爆发　 ▲　 周年。

A．50　 80　　　　　 B．50　 90　　　　　 C．60　 80　　　　 　D．60　 90

4.4 有关化学方程式(或热化学方程式)的计算

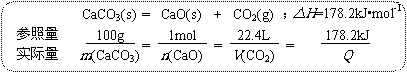
纵观上述计算，可以总结出基于比例关系的规范计算过程：

①列关系式：根据具体关系(组成、化学方程式等)列出关系式，注意化学计量数。

②写参照量：根据具体需要(物质的量、质量、微粒数、气体体积等)填写参照量(未知符号代替)。

③写实际量：对应参照量填写实际量(未知符号代替)，注意与纵列对应参照量的物理量一致。

④列比例式：在每一参照量与实际量之间添横线构成分式，在相邻分式之间添等号构成连等式。

⑤解比例式：根据已知量解出未知量。

⑥验证作答：检验解题结果是否正确，并按问题要求写出规范的答案。

实际上，基于比例关系的计算模型蕴含着一定的建模思想。

5 化学计算的模型巩固

在化学计算中，教材中的解法与教师的解法不同往往使很多学生产生顾虑，从而干扰了学生的计算学习，导致强化不够。我们认为，应该在适当的时候给学生以科学的“强心剂”，而不应只让学生“记住这个”，数学为我们提供了合理的工具，化学课堂同样需要数学证明，决不能把它看作是数学老师的工作。公式及比例式变形在有些老师看来就如“1+1=2”那么简单，但对于学生来说并非如此，因此在化学计算教学中同样需要强化。

公式及比例式的变形有其固有的数学道理--比例的性质定理(图3)，但学生对这些定理或不太熟悉，或认为这是数学的问题，我们认为有必要强化这些数学工具与化学计算之间的密切联系。

如初中化学教材中往往采用“参照量之比=实际量之比”的形式进行计算，表示为A:B:C=a:b:c；本文中所述的方法则是各个参照量与实际量之比之间建立连等式，表示为A/a=B/b=C/c。可利用小学数学中“等式的性质--等式两边同时乘(或除)相等的数或式子(不为零)，两边依然相等”进行分解与变形，或利用比例的换项定理进行证明，以消除学生的顾虑。

对于一些常用的计算技巧，也可以通过数学方法将以巩固，而不需破坏已形成的基于比例关系的计算模型。如差量法的计算既可通过代数方法(比例的等比定理)也可通过几何方法(平行线分线段成比例定理：三条平行线截两条直线所得对应线段成比例)予以证明。对于十字交叉法实际上不需要用这些冠名的解题技巧，但既可以通过代数的方法也可以使用物理的方法予以说明。如某浓溶液的质量为m₁，溶质的质量分数为x₁；某稀溶液的质量为m₂，溶质的质量分数为x₂；两溶液混合后溶质的质量分数为x。根据溶质总质量保持不变，则有：m₁x₁+m₂x₂=(m₁+m₂)x或m₁/m₂=(x-x₂)/(x₁-x)，其本质仍然是比例关系，且与初中物理中的杠杆平衡的条件完全一致，通过这样的方法理解特殊方法的计算技巧，既减少了学生死记硬背公式的做法，同时又强化了数学、物理和化学学科之间的统一和内在联系。

《化学教学》2009年第5期

4.3 有关溶液的计算

◆当利用溶质的质量分数(设为a%)进行溶液的计算时，可采用：

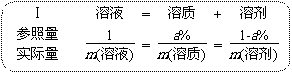
由此就可以得到计算溶质的质量分数的公式：a%=m(溶质)/m(溶液)。

◆当利用溶解度(S)进行饱和溶液的计算时，可采用：

由此就可以得到计算溶解度的公式：S=100m(溶质)/m(溶剂)。

◆当利用物质的量浓度(设为c mol•L^-1)进行溶液计算时，可采用：

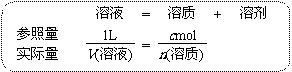
由此就可以得到计算物质的量浓度的公式：c=n(溶质)/V(溶液)。

4.2 有关化学式的计算

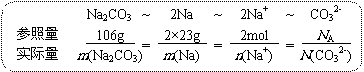
◆利用质量分数(Na₂CO₃中Na元素的质量分数为a%)进行计算时，则可以采用：

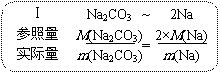
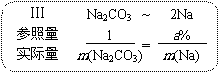
由此就可以得到计算元素质量分数的公式：a%=m(Na)/m(Na₂CO₃)=2M(Na)/M(Na₂CO₃)=2×23g/106g。

4.1 有关物质的量的计算

由此就可以得到相关的计算公式：n=m/M=V/V_m=N/N_A及其公式变形。

2.4 规范性

化学计算十分强调计算过程的规范性，在物质的量应用于化学方程式的计算时尤为突出。但由于化学计算涉及的概念广泛，公式及其变形众多，各种参考资料中的解题技法对规范解题没有统一的要求，从而导致解题多样化而缺乏统一规范的局面。

由于中学阶段化学计算的上述特征导致化学计算教学的非统一性，不同教师对化学计算的理解也存在差异，最终导致学生对化学计算仅仅停留在“依样画葫芦”的模仿水平，同时加上各种计算技巧的“狂轰滥炸”，常常会使学生在解决具体问题时“张冠李戴”。

3 化学计算的实质思考

我们认为，中学教学中的化学计算，不论是否牵涉有关概念，其本质都是一致的，都是基于比例关系而建立并发展的(表3)。

由此可见，各类计算都是基于比例关系建立的，因此在教学中应巩固这一共同的关系，构建统一的化学计算解题模式，从而使学生在化学计算所使用的方法形成固有的稳定结构。

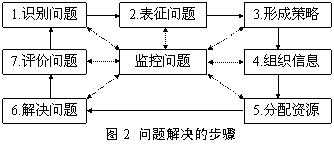
同时，化学计算的解题过程本质上就是问题解决的过程。人们在解决问题时，首先要从大脑中搜索与问题匹配的原型，如果不能找到原型就需要经过问题解决的一系列步骤(图2)来解决问题。事实上，问题识别是问题解决过程中最难的一步，让学生长期应用统一的解题模式无疑能有效地帮助学生缩短问题识别的时间，即使在碰到陌生问题时也不至于束手无策，也会尝试用这一统一的模式来解决。

4 化学计算的形式统一

基于对化学计算的比例本质的理解，我们尝试构造基于比例关系的化学计算形式。

2.3 综合性

考试大纲中特别强调了各类化学计算的综合应用，这就需要在方法论上下功夫。就化学计算的重要方法而言，就有关系式法、十字交叉法、守恒法、差量法、函数法、平均值法、极端假设法(极值法)、推理讨论法、整体思维法、归一法等等，再加上一些教辅资料中往往以一道例题对应一种方法来分析问题，导致解题方法种类繁多，平时训练中也不可能得到全面强化，其结果是解题名称一大堆，解题方法不熟练。在解决具体问题时，学生面对的则是琳琅满目的解题方法而不知所措。

2.2 概念性

由于中学化学计算中涉及很多的化学概念(表2)，相当多的考题，只要概念清晰，凭观察、心算或推算即可得到答案，一些有计算成分的选择题也往往是主要考查对基本概念的理解的。

正因为这些化学概念通常可以用数学公式来表示，导致学生在学习概念时死记硬背地记公式，解题时司空见惯地代公式，而忽视了概念本身的意义构建，这种简单的字母记忆并没有在本质上理解化学概念，其结果是概念不理解，公式记不牢。如在初中物理中十分强调的一个基本公式ρ=m/V，到了高中还有部分学生运用ρ=V/m、V=mρ等错误公式进行计算。

2.1 多样性

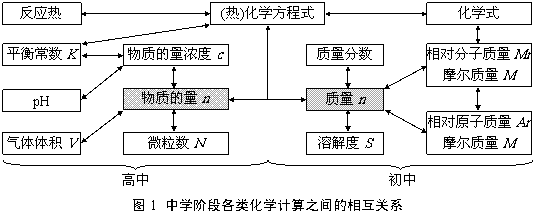
中学化学计算所包含的内容比较广，因此，化学计算考查的知识点也比较多。倘若稍加分析，可以发现，中学阶段所有的化学计算都是以2个基本物理量--物质的量和质量为核心结合化学概念和化学用语等而展开的(图1)。