
4.(★★★★)设a,b是异面直线,下列命题正确的是_________.
①过不在a、b上的一点P一定可以作一条直线和a、b都相交
②过不在a、b上的一点P一定可以作一个平面和a、b都垂直
③过a一定可以作一个平面与b垂直
④过a一定可以作一个平面与b平行
3.(★★★★★)设X、Y、Z是空间不同的直线或平面,对下面四种情形,使“X⊥Z且Y⊥Z X∥Y”为真命题的是_________(填序号).
X∥Y”为真命题的是_________(填序号).
①X、Y、Z是直线 ②X、Y是直线,Z是平面 ③Z是直线,X、Y是平面 ④X、Y、Z是平面
2.(★★★★)在直二面角α-l-β中,直线a α,直线b
α,直线b β,a、b与l斜交,则( )
β,a、b与l斜交,则( )
A.a不和b垂直,但可能a∥b B.a可能和b垂直,也可能a∥b
C.a不和b垂直,a也不和b平行 D.a不和b平行,但可能a⊥b
1.(★★★★)在长方体ABCD-A1B1C1D1中,底面是边长为2的正方形,高为4,则点A1到截面AB1D1的距离是( )
A.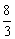 B.
B.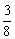 C.
C.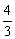 D.
D.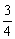
4.重视对数学思想、方法进行归纳提炼,达到优化解题思维、简化解题过程.
(1)方程思想
解析几何的题目大部分都以方程形式给定直线和圆锥曲线,因此把直线与圆锥曲线相交的弦长问题利用韦达定理进行整体处理,就简化解题运算量.
(2)用好函数思想方法
对于圆锥曲线上的一些动点,在变化过程中会引入一些相互联系、相互制约的量,从而使一些线的长度及a,b,c,e之间构成函数关系,函数思想在处理这类问题时就很有效.
(3)掌握坐标法
坐标法是解决有关圆锥曲线问题的基本方法.近几年都考查了坐标法,因此要加强坐标法的训练.
3.加强直线与圆锥曲线的位置关系问题的复习.此处一直为高考的热点.这类问题常涉及到圆锥曲线的性质和直线的基本知识点、线段的中点、弦长、垂直问题,因此分析问题时利用数形结合思想和设而不求法与弦长公式及韦达定理联系去解决.这样加强了对数学各种能力的考查.
2.重视求曲线的方程或曲线的轨迹,此处作为高考解答题的命题对象难度较大.所以要掌握住一般方法:定义法、直接法、待定系数法、相关点法、参数法等.
1.重点掌握椭圆、双曲线、抛物线的定义和性质.这些都是圆锥曲线的基石,高考中的题目都涉及到这些内容.
8.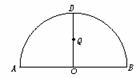 (★★★★★)如图,
(★★★★★)如图,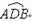 为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.
为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.
(1)建立适当的平面直角坐标系,求曲线C的方程;
(2)过D点的直线l与曲线C相交于不同的两点M、N,且M在D、N之间,设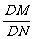 =λ,求λ的取值范围.
=λ,求λ的取值范围.
[学法指导]怎样学好圆锥曲线
圆锥曲线将几何与代数进行了完美结合.借助纯代数的解决手段研究曲线的概念和性质及直线与圆锥曲线的位置关系,从数学家笛卡尔开创了坐标系那天就已经开始.
高考中它依然是重点,主客观题必不可少,易、中、难题皆有.为此需要我们做到:
7.(★★★★★)已知抛物线C:y2=4x.
(1)若椭圆左焦点及相应的准线与抛物线C的焦点F及准线l分别重合,试求椭圆短轴端点B与焦点F连线中点P的轨迹方程;
(2)若M(m,0)是x轴上的一定点,Q是(1)所求轨迹上任一点,试问|MQ|有无最小值?若有,求出其值;若没有,说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com