
9.复合函数的求导法则:复合函数对自变量的导数,等于已知函数对中间变量的导数,乘以中间变量对自变量的导数

8.复合函数的导数:设函数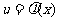 在点
在点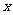 处有导数
处有导数 ,函数
,函数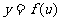 在点
在点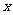 的对应点
的对应点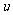 处有导数
处有导数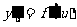 ,则复合函数
,则复合函数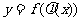 在点x处也有导数,且
在点x处也有导数,且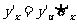 或
或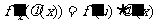
7.求导法则:法则
 .
.
法则
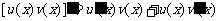 ,
, 
法则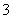 :
: 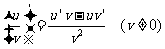
6.几种常见函数的导数:
 设函数
设函数 在
在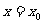 处附近有定义,当自变量在
处附近有定义,当自变量在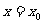 处有增量
处有增量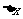 时,则函数
时,则函数 相应地有增量
相应地有增量 ,如果
,如果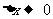 时,
时, 与
与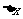 的比
的比 (也叫函数的平均变化率)有极限即
(也叫函数的平均变化率)有极限即 无限趋近于某个常数,我们把这个极限值叫做函数
无限趋近于某个常数,我们把这个极限值叫做函数 在
在 处的导数,记作
处的导数,记作
 导数的几何意义:
导数的几何意义:
导数 是函数
是函数 在点
在点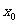 的处瞬时变化率,它反映的函数
的处瞬时变化率,它反映的函数 在点
在点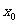 处变化的快慢程度.
处变化的快慢程度.
它的几何意义是曲线 上点(
上点( )处的切线的斜率.因此,如果
)处的切线的斜率.因此,如果 在点
在点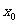 可导,则曲线
可导,则曲线 在点(
在点( )处的切线方程为
)处的切线方程为
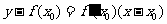
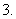 导函数(导数):如果函数
导函数(导数):如果函数 在开区间
在开区间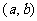 内的每点处都有导数,此时对于每一个
内的每点处都有导数,此时对于每一个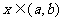 ,都对应着一个确定的导数
,都对应着一个确定的导数 ,从而构成了一个新的函数
,从而构成了一个新的函数 , 称这个函数
, 称这个函数 为函数
为函数 在开区间内的导函数,简称导数,也可记作
在开区间内的导函数,简称导数,也可记作 。
。
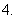 可导: 如果函数
可导: 如果函数 在开区间
在开区间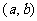 内每一点都有导数,则称函数
内每一点都有导数,则称函数 在开区间
在开区间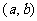 内可导
内可导
5.求函数 的导数的一般步骤:
的导数的一般步骤: 求函数的改变量
求函数的改变量
 求平均变化率
求平均变化率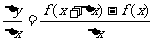 ;
; 取极限,得导数
取极限,得导数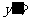


考纲点击: 了解导数概念的某些实际背景(如瞬时速度、加速度、光滑曲线切线的斜率等);
了解导数概念的某些实际背景(如瞬时速度、加速度、光滑曲线切线的斜率等); 掌握函数在一点处的导数的定义和导数的几何意义;
掌握函数在一点处的导数的定义和导数的几何意义; 理解导函数的概念
理解导函数的概念 熟记基本导数公式;
熟记基本导数公式;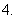 掌握两个函数和、差、积、商的求导法则;
掌握两个函数和、差、积、商的求导法则;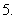 了解复合函数的求导法则
了解复合函数的求导法则 会求某些简单函数的导数;
会求某些简单函数的导数;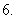 会求“过点
会求“过点 的曲线的切线方程”和“在点
的曲线的切线方程”和“在点 处的切线方程”.
处的切线方程”.
热点提示:导数的几何意义是高考考查重点,常以小题出现。导数的运算每年必考,一般不单独命题,在考查导数应用的同时考查导数的运算。
8.小华与小丽设计了 两种游戏:
两种游戏:
游戏 的规则:用3张数字分别是2,3,4的扑克牌,将牌洗匀后背面朝上放置在桌面上,第一次随机抽出一张牌记下数字后再原样放回,洗匀后再第二次随机抽出一张牌记下数字.若抽出的两张牌上的数字之和为偶数,则小华获胜;若两数字之和为奇数,则小丽获胜.
的规则:用3张数字分别是2,3,4的扑克牌,将牌洗匀后背面朝上放置在桌面上,第一次随机抽出一张牌记下数字后再原样放回,洗匀后再第二次随机抽出一张牌记下数字.若抽出的两张牌上的数字之和为偶数,则小华获胜;若两数字之和为奇数,则小丽获胜.
游戏 的规则:用4张数字分别是5,6,8,8的扑克牌,将牌洗匀后背面朝上放置在桌面上,小华先随机抽出一张牌,抽出的牌不放回,小丽从剩下的牌中再随机抽出一张牌.若小华抽出的牌面上的数字比小丽抽出的牌面上的数字大,则小华获胜;否则小丽获胜.
的规则:用4张数字分别是5,6,8,8的扑克牌,将牌洗匀后背面朝上放置在桌面上,小华先随机抽出一张牌,抽出的牌不放回,小丽从剩下的牌中再随机抽出一张牌.若小华抽出的牌面上的数字比小丽抽出的牌面上的数字大,则小华获胜;否则小丽获胜.
请你帮小丽选择其中一种游戏,使她获胜的可能性较大,并说明理由.
7.为了进一步了解九年级学生的身体素质情况,体育老师对九年级(1)班50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如下所示:
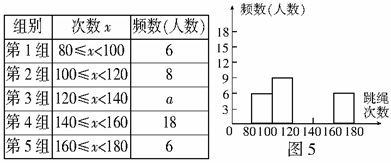
请结合图表完成下列问题:
(1)表中的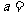 ___________;
___________;
(2)请把频数分布直方图补充完整;
(3)这个样本数据的中位数落在第________组;
(4)若九年级学生一分钟跳绳次数(x)达标要求是:x<120不合格;120≤x<140为合格;140≤x<160为良;x≥160为优.根据以上信息,请你给学校或九年级同学提一条合理化建议:___________________.
6.某市篮球队到市一中选拔一名队员.教练对王亮和李刚两名同学进行5次3分投篮测试,每人每次投10个球,图4记录的是这两名同学5次投篮中所投中的个数.
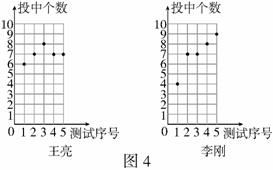
(1)请你根据图中的数据,填写下表.
|
姓名 |
平均数 |
众数 |
方差 |
|
王亮 |
|
7 |
|
|
李刚 |
7 |
|
2.8 |
(2)你认为谁的成绩比较稳定,为什么?
(3)若你是教练,你打算选谁?简要说明理由.
5.据统计,某州今年参加初三毕业会考的学生为46 000人.为了了解全州初三考生毕业会考数学考试情况,从中随机抽取了500名考生的数学成绩进行统计分析,在这个问题中,样本容量是________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com