
12.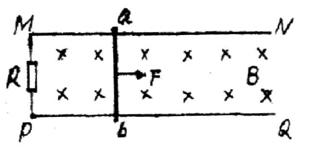 [临沂高新区]16.如图所示,MN和PQ为固定在水平面上的平行金属轨道,轨距为0.2m,质量为0.1kg的金属杆ab置于轨道上,与轨道垂直,整个装置处于方向竖直向下的匀强磁场中,磁感应强度B=0.5T,现用F=2N的水平向右的恒力拉ab杆由静止开始运动,电路中除了电阻R=0.05Ω之外,其余电阻不计,设轨道光滑,求:
[临沂高新区]16.如图所示,MN和PQ为固定在水平面上的平行金属轨道,轨距为0.2m,质量为0.1kg的金属杆ab置于轨道上,与轨道垂直,整个装置处于方向竖直向下的匀强磁场中,磁感应强度B=0.5T,现用F=2N的水平向右的恒力拉ab杆由静止开始运动,电路中除了电阻R=0.05Ω之外,其余电阻不计,设轨道光滑,求:
(1)ab杆的速度达到5m/s时的加速度多大?
(2)当ab杆达到最大速度后,撤去外力F,此后感应电流还能产生多少电热?
[解](1)ε=BLv=0.5×0.2×5V=0.5V
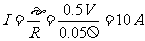
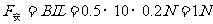
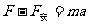
则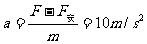
(2)

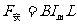
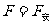
解以上各式得:

电热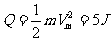
11.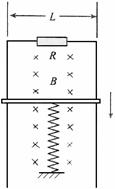 [临沭一中]18.(13分)如图所示,固定的竖直光滑金属导轨间距为L,上端接有阻值为R的电阻,处在方向水平、垂直导轨平面向里的磁感应强度为B的匀强磁场中,质量为m的导体棒与下端固定的竖直轻质弹簧相连且始终保持与导轨接触良好,导轨与导体棒的电阻均可忽略,弹簧的劲度系数为k。初始时刻,弹簧恰好处于自然长度,使导体棒以初动能Ek沿导轨竖直向下运动,且导体棒在往复运动过程中,始终与导轨垂直。
[临沭一中]18.(13分)如图所示,固定的竖直光滑金属导轨间距为L,上端接有阻值为R的电阻,处在方向水平、垂直导轨平面向里的磁感应强度为B的匀强磁场中,质量为m的导体棒与下端固定的竖直轻质弹簧相连且始终保持与导轨接触良好,导轨与导体棒的电阻均可忽略,弹簧的劲度系数为k。初始时刻,弹簧恰好处于自然长度,使导体棒以初动能Ek沿导轨竖直向下运动,且导体棒在往复运动过程中,始终与导轨垂直。
(1)求初始时刻导体棒所受安培力的大小F;
(2)导体棒往复运动一段时间后,最终将静止。设静止时弹簧的弹性势能为Ep,则从初始时刻到最终导体棒静止的过程中,电阻R上产生的焦耳热Q为多少?
[解](1)设导体棒的初速度为v0,由动能的定义式
 得
得 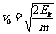 …………1分
…………1分
设初始时刻产生的感应电动势为E,由法拉第电磁感应定律得:
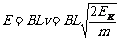 ………………2分
………………2分
设初始时刻回路中产生的电流为I,由闭合电路的欧姆定律得:
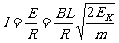 ………………2分
………………2分
设初始时刻导体棒受到的安培力为F,由安培力公式得:
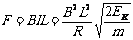 ………………2分
………………2分
(2)从初始时刻到最终导体棒静止的过程中,导体棒减少的机械能一部分转化为弹簧的弹性势能,另一部分通过克服安培力做功转化为电路中的电能,因在电路中只有电阻,电能最终全部转化为电阻上产生的焦耳热Q。……1分
当导体棒静止时,棒受力平衡,此时导体棒的位置比初始时刻降低了h,
则 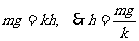 ………………2分
………………2分
由能的转化和守恒定律得: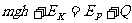 …………2分
…………2分
 …………2分
…………2分
10.[莱阳一中]21.(12分)如图(a)所示,两根足够长的光滑平行金属导轨相距为L=0.40m,导轨平而与水平面成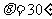 角,上端下端通过导线分别连接阻值
角,上端下端通过导线分别连接阻值 的电阻,
的电阻,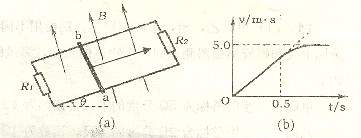 质量为m=0.20kg、阻值
质量为m=0.20kg、阻值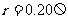 的金属棒ab放在两导轨上,棒与导轨垂直并保持良好接触,整个装置处在垂直导轨平面向上的匀强磁场中,磁感应强度大小B-1T。现通过小电动机对金属棒施加拉力,使金属棒沿导轨向上做匀加速直线运动,0.5s时电动机达到额定功率,此后电动机功率保持不变,经足够长时间后,棒达到最大速度5.
0m/s。此过程金属棒运动的
的金属棒ab放在两导轨上,棒与导轨垂直并保持良好接触,整个装置处在垂直导轨平面向上的匀强磁场中,磁感应强度大小B-1T。现通过小电动机对金属棒施加拉力,使金属棒沿导轨向上做匀加速直线运动,0.5s时电动机达到额定功率,此后电动机功率保持不变,经足够长时间后,棒达到最大速度5.
0m/s。此过程金属棒运动的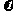 -t图象如图(b)所示,试求:(取重力加速度g=10m/
-t图象如图(b)所示,试求:(取重力加速度g=10m/ )
)
(1)电动机的额定功率P
(2)金属棒匀加速运动时的加速度a的大小
(3)在0-0.5s时间内电动机牵引力F与速度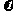 的关系
的关系
[解](1)达到最大速度时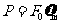 ………………………………1分
………………………………1分
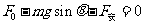 ………………………………1分
………………………………1分
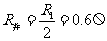 ………………………………1分
………………………………1分
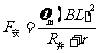 ………………………………1分
………………………………1分
由以上几式解得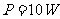 ………………………………1分
………………………………1分
(2) 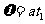 ………………………………1分
………………………………1分
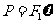 ………………………………1分
………………………………1分
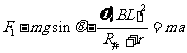 ………………………………1分
………………………………1分
解得 ………………………………1分
………………………………1分
(3) 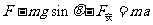 ………………………………1分
………………………………1分
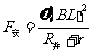 ………………………………1分
………………………………1分
解得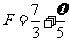 ………………………………1分
………………………………1分
9.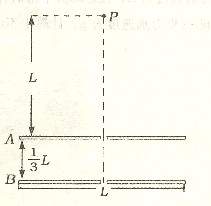 [莱阳一中]20.(10分) 如图所示,带有等量异种电荷的两平行金属板A和B水平放置,板间匀强电场的场强大小为E,方向竖直向下,两板正中央均开有小孔,板长为L,板间距离为L/3,整个装置处于真空环境中,在A板小孔正上方、距小孔为L处的P点,由静止释放一个带正电的小球(可看做质点),小球进入AB两板间时加速度变为原来的2倍,设小球通过上、下孔时的速度分别为
[莱阳一中]20.(10分) 如图所示,带有等量异种电荷的两平行金属板A和B水平放置,板间匀强电场的场强大小为E,方向竖直向下,两板正中央均开有小孔,板长为L,板间距离为L/3,整个装置处于真空环境中,在A板小孔正上方、距小孔为L处的P点,由静止释放一个带正电的小球(可看做质点),小球进入AB两板间时加速度变为原来的2倍,设小球通过上、下孔时的速度分别为 、
、 。现改变两板的带电性质,使两板间场强方向与原来相反,但大小不变,同时在两板之间加上垂直纸面向里的水平匀强磁场,再次在P点由静止释放该小球,小球从A板小孔进入两板间后,不碰撞极板而能从两板间飞出。求:(重力加速度为g)
。现改变两板的带电性质,使两板间场强方向与原来相反,但大小不变,同时在两板之间加上垂直纸面向里的水平匀强磁场,再次在P点由静止释放该小球,小球从A板小孔进入两板间后,不碰撞极板而能从两板间飞出。求:(重力加速度为g)
(1)  与
与 之比
之比
(2)磁感应强度B的取值范围
[解] (1)设小球电荷量为q,质量为m,
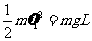 ①……………………………1分
①……………………………1分
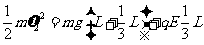 ②……………………………1分
②……………………………1分
由题意知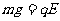 ③……………………………1分
③……………………………1分
联立①②③解得:
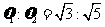 ④……………………………2分
④……………………………2分
(2)再次释放后,小球进入复合场之后做匀速圆周运动
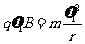 ⑤……………………………2分
⑤……………………………2分
要使小球不碰撞极板能飞出场区应满足
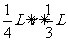 ⑥……………………………1分
⑥……………………………1分
联立①③⑤⑥解得:
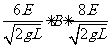 ⑦……………………………2分
⑦……………………………2分
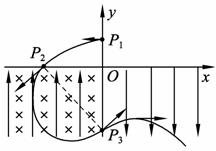
8.[济南市]15. (13分)如图所示的坐标系,x轴沿水平方向,y轴沿竖直方向。在x轴上方空间的第一、第二象限内,既无电场也无磁场,在第三象限,存在沿y轴正方向的匀强电场和垂直xy平面(纸面)向里的匀强磁场,在第四象限,存在沿y轴负方向、场强大小与第三象限电场场强相等的匀强电场。一质量为m、电荷量为q的带电质点,从y轴上y = h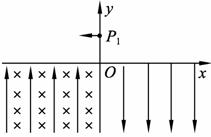 处的P1点以一定的水平初速度沿x轴负方向进入第二象限。然后经过x轴上x=-2h处的P2点进入第三象限,带电质点恰好能做匀速圆周运动。之后经过y轴上y=-2h处的P3点进入第四象限。已知重力加速度为g。试求:
处的P1点以一定的水平初速度沿x轴负方向进入第二象限。然后经过x轴上x=-2h处的P2点进入第三象限,带电质点恰好能做匀速圆周运动。之后经过y轴上y=-2h处的P3点进入第四象限。已知重力加速度为g。试求:
(1) 粒子到达P2点时速度的大小和方向
(2) 第三象限空间中电场强度和磁感应强度的大小
(3) 带电质点在第四象限空间运动过程中最小速度的大小和方向。
[解](1) 参见图,带电质点从P1到P2,由平抛运动规律
 h=
h=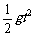 ①(1分)
①(1分)
v0=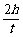 ②(1分)
②(1分)
vy=gt ③(1分)
求出v=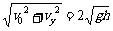 ④(1分)
④(1分)
方向与x轴负方向成45°角(1分)
用其它方法求出正确答案的同样给分。
(2) 带电质点从P2到P3,重力与电场力平衡,洛伦兹力提供向心力
Eq=mg ⑤(1分)
Bqv=m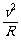 ⑥(1分)
⑥(1分)
(2R)2=(2h)2+(2h)2 ⑦(1分)
由⑤解得:E=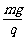 ⑧(1分)
⑧(1分)
联立④⑥⑦式得B=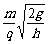 ⑨(1分)
⑨(1分)
(3) 带电质点进入第四象限,水平方向做匀速直线运动,竖直方向做匀减速直线运动。当竖直方向的速度减小到0,此时质点速度最小,即v在水平方向的分量
vmin=vcos45°=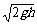 ⑩(2分)
⑩(2分)
方向沿x轴正方向(1分)
7. [济南市]13.
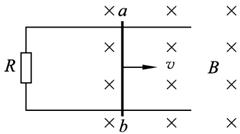
(8分)如图所示,一水平放置的平行导体框架宽度L=0.5 m,接有电阻R=0.20 Ω,磁感应强度B=0.40
T的匀强磁场垂直导轨平面方向向下,仅有一导体棒ab跨放在框架上,并能无摩擦地沿框架滑动,框架及导体ab电阻不计,当ab以v=4.0
m/s的速度向右匀速滑动时。试求:
[济南市]13.
(8分)如图所示,一水平放置的平行导体框架宽度L=0.5 m,接有电阻R=0.20 Ω,磁感应强度B=0.40
T的匀强磁场垂直导轨平面方向向下,仅有一导体棒ab跨放在框架上,并能无摩擦地沿框架滑动,框架及导体ab电阻不计,当ab以v=4.0
m/s的速度向右匀速滑动时。试求:
(1) 导体ab上的感应电动势的大小。
(2) 要维持ab向右匀速运行,作用在ab上的水平力为多大?
(3) 电阻R上产生的焦耳热功率为多大?
[解](1) 导体ab垂直切割磁感线,产生的电动势大小:
E=BLv=0.40×0.50×4.0 V=0.80 V ①(2分)
(2) 导体ab相当于电源,由闭合电路欧姆定律得回路电流:
I=ER+r=0.800.20+0 A=4.0 A ②(1分)
导体ab所受的安培力:
F=BIL=0.40×4.0×0.50 N=0.80 N ③(1分)
由于ab匀速运动,所以水平拉力:
F′=F=0.80 N ④(2分)
(3) R上的焦耳热功率:
P=I2R=4.02×0.20 W=3.2 W ⑤(2分)
6.[日照市]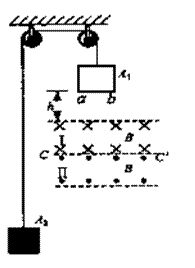
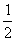 (M+m)v
(M+m)v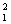 ①(2分)
①(2分)
解得v1=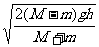 ②(2分)
②(2分)
(2)设线框ab边进入磁场Ⅱ时速度为v2,则线框中产生的感应电动势:
E=2BLv2 ③(1分)
线框中的电流I=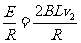 ④(1分)
④(1分)
线框受到的安培力F=2IBL=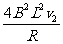 ⑤(2分)
⑤(2分)
设绳对A1、A2的拉力大小为T,则:
对A1:T+F=Mg ⑥(1分)
对A2:T=mg ⑦(1分)
联立⑤⑥⑦解得:v2=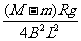 ⑧(2分)
⑧(2分)
5.[苍山县]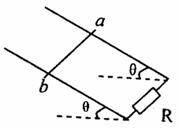 17.(13分)如图所示,处于匀强磁场中的两根足够长、电阻不计的平行金属导轨相距
17.(13分)如图所示,处于匀强磁场中的两根足够长、电阻不计的平行金属导轨相距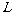 =1m,导轨平面与水平面成
=1m,导轨平面与水平面成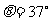 角,下端连接阻值为
角,下端连接阻值为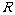 的电阻。匀强磁场方向与导轨平面垂直。质量为
的电阻。匀强磁场方向与导轨平面垂直。质量为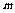 =0.2kg,电阻不计的金属棒
=0.2kg,电阻不计的金属棒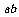 放在两导轨上,棒与导轨垂直并保持良好接触,它们之间的动摩擦因数为
放在两导轨上,棒与导轨垂直并保持良好接触,它们之间的动摩擦因数为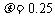 。(设最大静摩擦力大小等于滑动摩擦力大小,且g取10m/s2,sin37°=0.6,cos37°=0.8)。求:
。(设最大静摩擦力大小等于滑动摩擦力大小,且g取10m/s2,sin37°=0.6,cos37°=0.8)。求:
(1)金属棒沿导轨由静止开始下滑时加速度a的大小
(2)当金属棒下滑速度达到稳定时,电阻R消耗的功率为8W,则此时金属棒速度 的大小
的大小
(3)上问中,若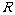 =2Ω,金属棒中的电流方向由
=2Ω,金属棒中的电流方向由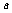 到
到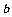 ,则磁感应强度
,则磁感应强度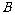 的大小和方向。
的大小和方向。
[解](1)根据牛顿第二定律 ①(2分)
①(2分)
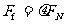 ②
②
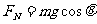 ③(1分)
③(1分)
联立①②③得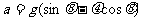 =4m/s2 ④(1分)
=4m/s2 ④(1分)
(2)设金属棒运动达到稳定时,速度为v,所受安培力为F,棒在沿导轨方向受力平衡
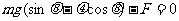 ⑤(2分)
⑤(2分)
此时金属棒克服安培力做功的功率P等于电路中电阻R消耗的电功率
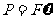 ⑥ (1分)
⑥ (1分)
由⑤⑥两式解得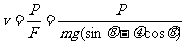
将已知数据代入上式得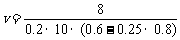 =10m/s (1分)
=10m/s (1分)
(3)设电路中电流为I,两导轨间金属棒的长为L,磁场的磁感应强度为B
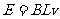 (1分)
(1分)
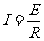 (1分)
(1分)
 (1分)
(1分)
由以上三式解得 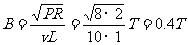 (1分)
(1分)
磁场方向垂直导轨平面向上 (1分)
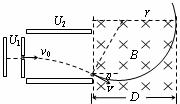
4.[苍山县]16.(12分)如图所示,一个质量为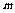 =2.0×10-11kg,电荷量
=2.0×10-11kg,电荷量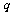 = +1.0×10-5C的带电微粒(重力忽略不计),从静止开始经U1=100V电压加速后,水平进入两平行金属板间的偏转电场,偏转电场的电压U2=100V。金属板长L=20cm,两板间距d =
= +1.0×10-5C的带电微粒(重力忽略不计),从静止开始经U1=100V电压加速后,水平进入两平行金属板间的偏转电场,偏转电场的电压U2=100V。金属板长L=20cm,两板间距d =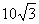 cm。求:
cm。求:
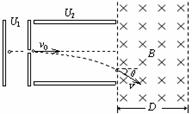 (1)微粒进入偏转电场时的速度
(1)微粒进入偏转电场时的速度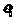 大小
大小
(2)微粒射出偏转电场时的偏转角
(3)若该匀强磁场的磁感应强度B =0.346T,
为使微粒不会由磁场右边射出,该匀强磁场的
宽度D至少为多大
[解](1)微粒在加速电场中由动能定理得
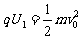 解得v0=1.0×104m/s (2分)
解得v0=1.0×104m/s (2分)
(2)微粒在偏转电场中做类平抛运动,有
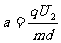 ,
,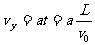 (2分)
(2分)
飞出电场时,速度偏转角的正切为
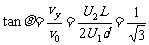 解得 θ=30o (2分)
解得 θ=30o (2分)
(3)进入磁场时微粒的速度是: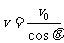 (2分)
(2分)
轨迹如图,由几何关系有: (1分)
(1分)
 洛伦兹力提供向心力:
洛伦兹力提供向心力: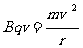 (2分)
(2分)
联立以上三式得 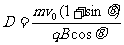
代入数据解得 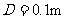 (1分)
(1分)
3.[聊城市]17.(12分)如图所示,地面附近的坐标系xoy在竖直平面内,空气有沿水平方向垂直于纸面向里、磁感应强度大小为B的匀强磁场,在x<0的空间内还有沿x轴负方向、场强大小为E的匀强电场。一个带正电的油滴经图中x轴上的M点,沿与水平方向成a=30°角斜向下的直线运动,进入x>0的区域。要使油滴进入x>0的区域后能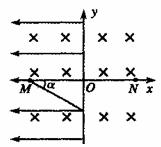 在竖直平面内做匀速圆周运动,需在x>0区域加一个匀强电场。若带电油滴做圆周运动通过x轴上的N点,且MO=ON,重力加速度为g,求:
在竖直平面内做匀速圆周运动,需在x>0区域加一个匀强电场。若带电油滴做圆周运动通过x轴上的N点,且MO=ON,重力加速度为g,求:
(1)油滴运动的速度大小;
(2)在x>0区域内所加电场的场强大小及方向;
(3)油滴从M点到N点所用的时间。
[解](1)带电油滴在x<0区域内受重力mg,电场力qE和洛仑兹力f,油滴沿直线运动,重力和电场力为恒力,则与运动方向垂直的洛仑兹力f的大小一定不能变化,因此油滴一定做匀速直线运动。
由平衡条件可知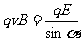 ①
①
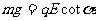 ②
②
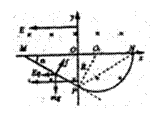 由①②两式得
由①②两式得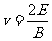 ③
③
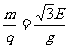 ④
④
(2)因油滴进入x>0区域后做匀速圆周运动,
所受电场力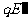 与重力等大方向,
与重力等大方向,
即 ⑤
⑤
由④⑤得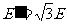 ⑥
⑥
(3)油滴从P点进入x>0区域,然后做匀速圆周运动,其轨迹所对应的圆心角为
120°,油滴从P到N的时间
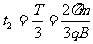 ⑦
⑦
由④⑦得: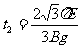 ⑧
⑧
由几何关系可知:图中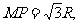 油滴从M到P的时间
油滴从M到P的时间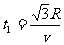 ⑨
⑨
又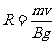 ⑩
⑩
又④⑨⑩得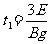 11
11
从M到N的总时间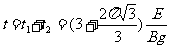 12
12
评分标准:以上各式每式1分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com