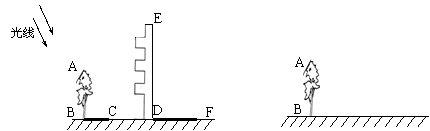
22、高为12.6米的教学楼ED前有一棵大树AB(如图1)．

(1)某一时刻测得大树AB、教学楼ED在阳光下的投影长分别是BC=2.4米，DF=7.2米，求大树AB的高度．

(2)用皮尺、高为h米的测角仪，请你设计另一种测量大树AB高度的方案，要求：

①在图2上，画出你设计的测量方案示意图，并将应测数据标记在图上(长度用字母m 、n …表示，角度用希腊字母α、β …表示)；

②根据你所画的示意图和标注的数据，计算大树AB高度(用字母表示)．

21、为响应承办“绿色奥运”的号召，某中学初三、2班计划组织部分同学义务植树180棵，由于同学们参与的积极性很高，实际参加植树活动的人数比原计划增加了50%，结果每人比原计划少栽了2棵树，问实际有多少人参加了这次植树活动？

20、李红和张明正在玩掷骰子游戏，两人各掷一枚骰子。

⑴当两枚骰子点数之积为奇数时，李红得3分，否则，张明得1分，这个游戏公平吗？为什么？

⑵当两枚骰子的点数之和大于7时，李红得1分，否则张明得1分，这个游戏公平吗？为什么？如果不公平，请你提出一个对双方公平的意见。

19、某校研究性学习小组在研究相似图形时，发现相似三角形的定义、判定及其性质，可以拓展到扇形的相似中去。例如，可以定义：“圆心角相等且半径和弧长对应成比例的两个扇形叫做相似扇形”；相似扇形有性质：弧长比等于半径比、面积比等于半径比的平方…。请你协助他们探索这个问题。

(1)　　　 写出判定扇形相似的一种方法：若_____________________________，则两个扇形相似；

(2)　　　 有两个圆心角相等的扇形，其中一个半径为a、弧长为m，另一个半径为2a，则它的弧长为_________________；

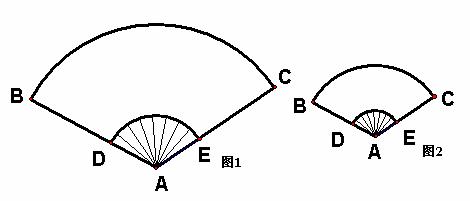
(3)　　　 如图1是一完全打开的纸扇，外侧两竹条AB和AC的夹角为120°，AB为30cm，现要做一个和它形状相同、面积是它一半的纸扇(如图2)，求新做纸扇(扇形)的圆心角和半径。

18、大楼AD的高为10米，远处有一塔BC，某人在楼底A处测得踏顶B处的仰角为60º，爬到楼顶D点测得塔顶B点的仰角为30º，求塔BC的高度。

17、已知不等式：⑴1－x＜0；⑵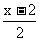＜1；⑶　 2x+3＞1；⑷　 0.2x－3＜－2．你喜欢其中哪两个不等式，请把它们选出来组成一个不等式组，求出它的解集，并在数轴上把解集表示出来．

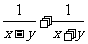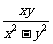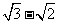16、先化简，再求值：()÷，其中x＝　y＝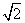

15、如图，已知，在△ABC和△DCB中，AC=DB，

若不增加任何字母与辅助线，要使△ABC≌△DCB，

则还需增加一个条件是　　　　　 .

14、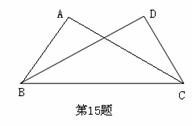甲、乙两个同学在几次测验中，平均分都是86分，甲的方差是0.61，乙的方差是0.72，则可知成绩较稳定情况是　　　　　 .

(填甲或乙或一样)稳定。

13、一家皮鞋店，购进同一品牌的8双皮鞋尺码(单位：㎝)依次为：22，22.5，23.5，23.5，23.5，24，24.5，则这组数据的众数是　　　　　　 ㎝.