2．ABCD是平行四边形，已知点A(-1，3)和C(-3，2)，点D在直线x-3y-1=0上移动，则点B的轨迹方程是

1．一个以原点为圆心的圆与圆：x²+y²+8x-4y=0关于直线l对称，求直线l的方程．

(2x-y+5=0)

3．通过对称问题的探讨，使学生会进一步运用运动变化的观点，用转化的思想来处理问题．

教学重点与难点

两曲线关于定点和定直线的对称知识方法是重点．把数学问题转化为对称问题，即用对称观点解决实际问题是难点．

教学过程

师：前面学过了几种常见的曲线方程，并讨论了曲线的性质．今天这节课继续讨论有关对称的问题．大家想一想：点P(x，y)、P′(x′，y′)关于点Q(x₀，y₀)对称，那么它们的坐标应满足什么条件？

师：P(x，y)，P′(x′，y′)关于原点对称，那么它们的坐标满足什么条件？

生：P和P′的中点是原点．即x=-x′且y=-y′．

师：若P和P′关于x轴对称，它们的坐标又怎样呢？

生：x=x′且y=-y′．

师：若P和P′关于y轴对称，它们的坐标有什么关系？

生：y=y′且x=-x′．

师：若P和P′关于直线y=x对称，它们的坐标又会怎样？

生：y=x′且x=y′．

生：它们关于直线y=x对称．

师：若P与P′关于直线Ax+By+C=0对称，它们在位置上有什么特征？

生：P和P′必须在直线Ax+By+C=0的两侧．

师：还有补充吗？

生：PP′的连线一定与直线Ax+By+C=0垂直．

师：P与P′在直线Ax+By+C=0的两侧且与直线垂直就能对称了吗？

生：还需要保证P和P′到直线Ax+By+C=0的距离相等．

师：P与P′到直线Ax+By+C=0的距离相等的含义是什么？

生：就是P与P′的中点落在直线Ax+By+C=0上，换句话说P与P′的中点坐标满足直线方程Ax+By+C=0．

师：下面谁来总结一下，两点P(x，y)、P′(x′，y′)关于直线Ax+By+C=0对称应满足的条件？

生：应满足两个条件．第一个条件是PP′的连线垂直于直线Ax+By+C=0，第二个条件是P，P′的中点应落在直线Ax+By+C=0上．

师：这两个条件能否用方程表示呢？

(在黑板上可画出图形(如图2-72)，可直观些)

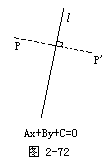
生：方程组：

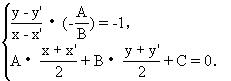
师：这个方程组成立说明了什么？它能解决什么问题？

生：方程组中含有x′，y′，也可认为这是一个含x′，y′的二元一次方程组．换句话说，给定一个点P(x，y)和一条定直线Ax+By+C=0，可以求出P点关于直线Ax+By+C=0的对称点P′(x′，y′)的坐标．

师：今后有很多有关对称问题都可以用此方法处理，很有代表性．但也还有其他方法，大家一起看下面的例题．

例1　 已知直线l₁和l₂关于直线2x-2y+1=0对称(如图2-73)，若l₁的方程是3x-2y+1=0，求l₂的方程．

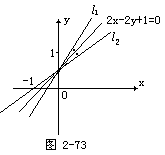
(选题目的：熟悉对称直线方程)

师：哪位同学有思路请谈谈．

生：先求出已知两直线的交点，设l₂的斜率为k，由两条直线的夹角公式可求出k，再用点斜式求得l₂的方程．

(让这位同学在黑板上把解题的过程写出来，大家订正．)

由点斜式，l₂的方程为4x-6y+3=0．

师：还有别的解法吗？

生：在直线l₁上任取一点，求出这点关于2x-2y+1=0对称的点，然后再利用交点，两点式可求出l₂的直线方程。

(让这位学生在黑板上把解题过程写出来，如有错误，大家订正．)

解　 由方程组：

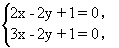
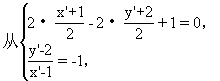
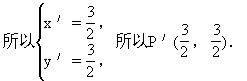
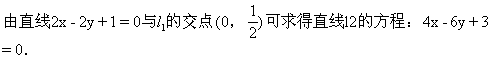
师：还有别的解法吗？

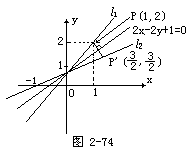
生：在l₂上任取一点P(x，y)，则P点关于2x-2y+1=0对称的点P′(x′，y′)在l₁上，列出P，P′的方程组，解出x′，y′，代入l₁问题就解决了．

师：请你到黑板上把解题过程写出来．

解　 设P(x，y)为l₂上的任意一点，

则P点关于直线2x-2y+1=0对称，点P′(x′，y′)在l₁上(如图2-75)，

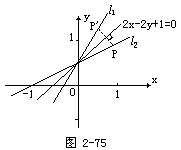
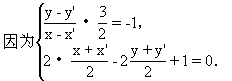
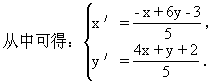
又因为P′(x′，y′)在直线l₁：3x-2y+1=0上，

所以3·x′-2y′+1=0．

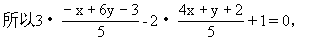
即l₂的方程为：4x-6y+3=0．

师：很好，大家刚才的几种解法是求对称直线方程的常规方法．那么，如果把l₁改为曲线，怎样求曲线关于一条直线对称的曲线方程呢？

引申：已知：曲线C：y=x²，求它关于直线x-y-2=0对称的曲线方程．

(选题目的：进一步熟悉对称曲线方程的一般方法．)

师：例1中的几种解法还都适用吗？

生：第二种和第三种方法还能适用．

师：谁来试一试？

生：可先在y=x²上任取一点P₀(x₀，y₀)，它关于直线的对称点P′(x₁，y₁)，可得它们的交点，从中解出x₀，y₀代入曲线y=x²即可(如图2-76)．

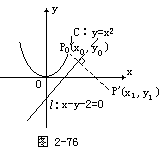
(让学生把他的解法写出来．)

解　 设P₀(x₀，y₀)是曲线C：y=x²上任意一点，它关于直线x-y-2=0对称的点为P′(x₁，y₁)，因此，连结P₀(x₀，y₀)和P′(x₁，y₁)两点的直线方程为y-y₀=-(x-x₀)．

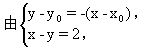
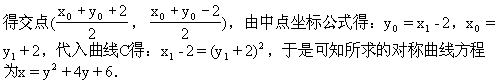
师：还有不同的方法吗？

生：用两点关于直线对称的方法也能解决．

师：把你的解法写在黑板上．

生：解：设M(x，y)为所求的曲线上任一点，M₀(x₀，y₀)是M关于直线x-y-2=0对称的点，所以M₀定在曲线C：y=x²上．

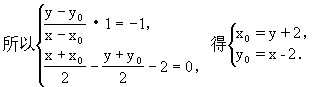
代入C的方程可得x=4y²+4y+6．

师：大家再看一个例子．

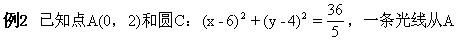
点出发射到x轴上后，沿圆的切线方向反射，求这条光线从A点到切点所经过的路程．(如图2-77)

师：解这题的关键是什么？

生：关键是找到x轴的交点．

师：有办法找到交点吗？

生：没人回答．

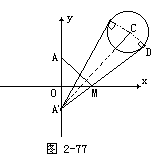
师：交点不好找，那么我们先假设M就是交点，利用交点M对解决这个问题有什么帮助吗？

生：既然AM是入射光线，MD为反射光线，D为切点，这样入射角就等于反射角，从而能推出∠AMO=∠DMx．

师：我们要求|AM|+|MD|能解决吗？

生：可以先找A关于x轴的对称点A′(0，-2)，由对称的特征知：|AM|=|A′M|，这样把求|AM|+|MD|就可以转化为|A′M|+|MD|即|A′D|．

师：|A′D|怎么求呢？

生：|A′D|实际上是过A′点到圆切线的长，要求切线长，只需先连结半径CD，再连结A′C，在Rt△A′CD，|CD|和|A′C|都已知，|AD|就可以得到了．(如图2-77)

(让这位学生把解答写在黑板上．)

解　 已知点A关于x轴的对称点为A′(0，-2)，所求的路程即为

师：巧用对称性，化简了计算，很好．哪位同学能把这个题适当改一下，变成另一个题目．

生：若已知A(0，2)，D(4，1)两定点，在x轴上，求一点P，使得|AP|+|PD|为最短．

师：谁能解答这个问题？

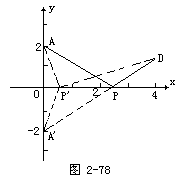
生：先过A(0，2)关于x轴的对称点A′(0，-2)，

连结A′D与x轴相交于点P，P为所求(如图2-78)．

师：你能保证|AP|+|PD|最短吗？

生：因为A，A′关于x轴对称，所以|AP|=|A′P|，这时|AP|+|PD|=|A′D|为线段，当P点在x轴其他位置上时，如在P′处，那么，连结AP′、A′P′和P′D．这时|AP′|+|P′D|=|A′P|+|P′D|＞|A′D|．理由(三角形两边之和大于第三边)．所以|A′D|为最短．即P为所求．

师：这题还能不能再做些变形，使之成为另一个题目？

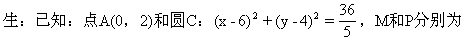
x轴和圆C上的动点，求|AM|+|MP|的最小值．

师：哪位同学能够解决？

生：先作A点关于x轴的对称点A′(0，-2)，连结A′和圆心C，A′C交x轴于M点，交圆于P点，这时|AM|+|MP|最小(如图2-79)．

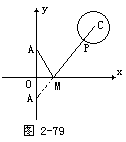
师：你怎样想到先找A点关于x轴的对称点A′的呢？

生：由前题的结论可知，把AM线段搬到x轴下方，尽可能使它们成为直线，这样|A′M|+|MP|最小．

师：很好，大家一起动笔算一算(同时让这位学生上前面书写)．

生：解A点关于x轴的对称点为A′(0，-2)，连A′C交x轴于M，交圆C于P点，因为A′(0，-2)，C(6，4)，所以|A′C|=

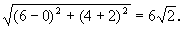
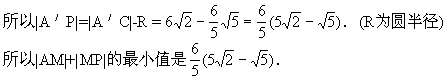
师：我们一起看下面的问题．

例3　 若抛物线y=a·x²-1上总存在关于直线x+y=0对称的两点，求a的范围．

师：这题的思路是什么？

生：如图2-80，设A(x₁，y₁)，B(x₂，y₂)是抛物线上关于直线x=-

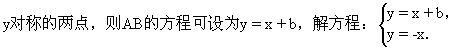
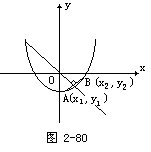
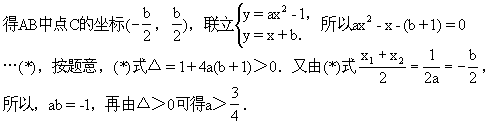
师：很好，谁还有不同的解法吗？

生：曲线y=ax²-1关于直线x+y=0对称曲线方程为：-x=ay²-1，解方

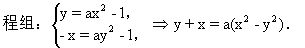
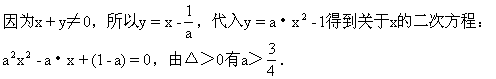
师：今天我们讨论了有关点，直线，曲线关于定点，定直线，对称的问题．解决这些问题的关键所在就是牢固掌握灵活运用两点关于定直线对称的思想方法，结合图象利用数形结合思想解决问题．

作业：

2．通过对称问题的研究求解，进一步理解数形结合的思想方法，提高分析问题和解决问题的能力．

1．引导学生探索并掌握解决中心对称及轴对称问题的解析方法．

22、(而)况……乎　译为“何况……呢”或“又何况……呢”

例：今以钟磬置水中，虽大风浪不能鸣也，而况石乎！

译文：现在把钟和磬放入水中，即使有大风大浪也不能使它发出声响，又何况是石头呢？

13. "非惟……抑亦"连用，表递进，相当于现代汉语"不只……而且"。 例：非惟天时，抑亦人谋也。(陈寿《隆中对》)译文：不只是时机好，而且也是人的谋划得当啊。

11、"非……而……"连用，表判断，相当于现代汉语的"不是……而是"。 例：非字而画。(《促织》)译文：(纸片上面)不是写的字，而是画的画。 12. "以……为"连用，表判断，相当于现代汉语的"认为……"、"把……当作"、"凭借(依靠)……作为"等。 例： 以天下之美，为尽在己。(《庄子·秋水》)　 译文：认为天下最美丽壮观的东西都集中在自己身上。 例： 而蔺相如徒以口舌为劳，而位居我上。(《廉颇蔺相如列传》) 译文：可是蔺相如仅仅只凭借一点说话的技巧作为功劳，职位却在我的上面

10、非……则……　　 可译为：“不是……就是”

7、无以……　 ；有以……

这是两个意义相反的固定结构。它们用在谓语动词前，相当于助动词的作用。可分别译为“有用来……的……”、“没有……的……”。 　 例：臣乃得有以报太子。(《荆轲刺秦王》)译文：我才能有用来报答太子的(机会)。

例：吾终当有以活汝。(《中山狼传》)--我总会有可以拿来使你活下去的方法。 例：军中无以为乐。(《鸿门宴》)--军营里没有可以用来作乐的东西……

例：故不积跬步，无以至千里；不积小流，无以成江海。--因此不积累小步，就无法达到千里之外；不世集细微的水流，就无法形成江海。