
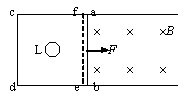
13.(09年上海物理)如图,金属棒ab置于水平放置的U形光滑导轨上,在ef右侧存在有界匀强磁场B,磁场方向垂直导轨平面向下,在ef左侧的无磁场区域cdef内有一半径很小的金属圆环L,圆环与导轨在同一平面内。当金属棒ab在水平恒力F作用下从磁场左边界ef处由静止开始向右运动后,圆环L有__________(填收缩、扩张)趋势,圆环内产生的感应电流_______________(填变大、变小、不变)。
答案:收缩,变小
解析:由于金属棒ab在恒力F的作用下向右运动,则abcd回路中产生逆时针方向的感应电流,则在圆环处产生垂直于只面向外的磁场,随着金属棒向右加速运动,圆环的磁通量将增大,依据楞次定律可知,圆环将有收缩的趋势以阻碍圆环的磁通量将增大;又由于金属棒向右运动的加速度减小,单位时间内磁通量的变化率减小,所以在圆环中产生的感应电流不断减小。
24、(原创)(本小题满分12分)
开口向下的抛物线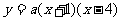 与
与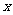 轴的交点为A、B(A在B的左边),
轴的交点为A、B(A在B的左边),
与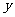 轴交于点C。连结AC、BC。
轴交于点C。连结AC、BC。
(1) 若△ABC是直角三角形(图1)。求二次函数的解析式;
(2) 在(1)的条件下,将抛物线沿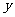 轴的负半轴向下平移
轴的负半轴向下平移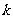 (
(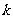 >0)个单位,
>0)个单位,
使平移后的抛物线与坐标轴只有两个交点。求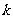 的值。
的值。
(3) 当点C坐标为(0,4)时(图2),P、Q两点同时从C点出发,点P沿折线C→O→B运
动到点B,点Q沿抛物线(在第一象限的部分)运动到点B,若P、Q两点的运动速度相

 同,请问谁先到达点B?请说明理由.(参考数据:
同,请问谁先到达点B?请说明理由.(参考数据: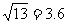
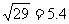 )
)
命题:萧山区金山学校 来小权
23、(原创)(本小题满分10分)
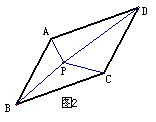
⑴如图1,点P是平行四边形ABCD对角线AC、BD的交点,若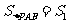 ,
,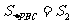 ,
,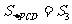 ,
,
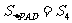 则
则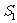 、
、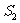 、
、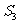 、
、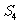 的关系为
的关系为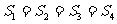 。请你说明理由
。请你说明理由
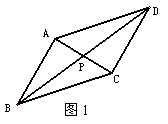
⑵变式1:如图2,点P是平行四边形ABCD内一点,连接PA、PB、PC、PD。若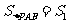 ,
,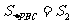 ,
,
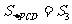 ,
,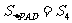 则
则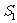 、
、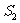 、
、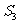 、
、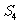 的关系为
。
的关系为
。
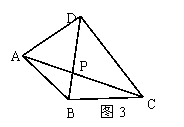
⑶变式2:如图3,点P是四边形ABCD对角线AC、BD的交点若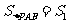 ,
,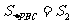 ,
,
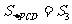 ,
,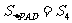 则
则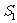 、
、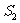 、
、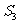 、
、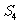 的关系为
。请你说明理由
的关系为
。请你说明理由
22、(原创)(本小题满分10分)
某公司需在一个月(31天)内完成新建办公楼的装修工程。若甲、乙两个工程队合作8天,
则其余的工作乙要10天才能完成,这样共需装修费用为41200元;若甲先做10天.,然后乙做
15天才能完成这工程,这样共需装修费用为41000元。
(1) 只要求在规定的时间内完成工程,若只请一个工程队,请问可以请哪个工程队?
(2) 在规定的时间内完成工程,按 方案 A:单独请一个工程队单独完成此项工程;
方案B、:请甲、乙两个工程队合作完成此项工程。 试问哪一种方案花钱少?
21、(09黄石)(本小题满分8分)
全国实施“限塑令”于2010年6月1日满二年,某报三名记者当日分别在杭州三大商业集
团门口,同时采用问卷调查的方式,随机调查了一定数量的顾客,在“限塑令”实施前后使用
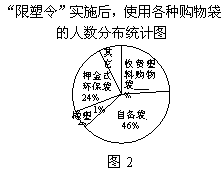
购物袋的情况.下面是这三名记者根据汇总的数据绘制的统计图.
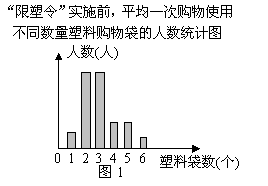


请你根据以上信息解答下列问题
(1)图1中从左到右各长方形的高度之比为2∶8∶8∶3∶3∶1,又知此次调查中
使用4个和5个塑料购物袋的顾客一共24人,问这三名记者一共调查了多少人?
(2)“限塑令”实施前,如果每天约有6000人到该三大商场购物,根据记者所调查的
一定数量顾客平均一次购物使用塑料购物袋的平均数,估计这三大商业集团每天需要为
顾客提供多少个塑料购物袋?
20、(08邵阳)(本小题满分8分)
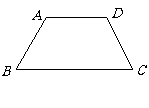
学生在讨论命题:“如图,梯形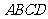 中,
中,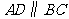 ,
,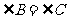 ,则
,则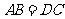 .”的
.”的
 证明方法时,提出了如下三种思路.
证明方法时,提出了如下三种思路.
思路1:过一个顶点作另一腰的平行线,转化为等腰三角形和平行四边形
思路2:延长两腰相交于一点,转化为等腰三角形.
思路3:过同一底边上的顶点作另一条底边的垂线,转化为直角三角形和矩形
请你结合以上思路,用适当的方法证明该命题.
19、(原创)(本小题满分6分)
用一条直线可将等腰梯形分成两部分,用这两部分能拼成一个新的图形。
请你在原等腰梯形上画出直线,并对这条直线进行必要的说明,然后在框内画出要求的新图形

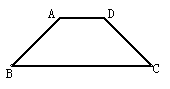 (1)将等腰梯形分割后拼成矩形
(1)将等腰梯形分割后拼成矩形
 (2)将等腰梯形分割后拼成平行四边形(非矩形)
(2)将等腰梯形分割后拼成平行四边形(非矩形)

 (3)将等腰梯形分割后拼成三角形
(3)将等腰梯形分割后拼成三角形

18、(09舟山)(本小题满分6分)
给出三个整式a2,b2和2ab.
(1) 当a=3,b=4时,求a2+b2+2ab的值;
(2) 在上面的三个整式中任意选择两个整式进行加法或减法运算,
使所得的多项式能够因式分解.请写出你所选的式子及因式分解的过程.
解答应写出文字说明、证明过程或推演步骤。如果觉得有的题目有困难,
那么把自己能写出的解答写出一部分也可以。
17、(09安徽)(本小题满分6分)
观察下列等式: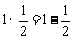 ,
,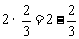 ,
,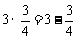 ,……
,……
(1)猜想并写出第n个等式; (2)证明你写出的等式的正确性.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com