
20.已知a , b都是正数,△ABC在平面直角坐标系xOy内, 以两点A (a ,0 )和B (0,b )为顶点的正三角形,且它的第三个顶点C在第一象限内.
(1)若△ABC能含于正方形D = { ( x , y ) | 0 £ x £ 1, 0£ y £ 1}内, 试求变量 a , b 的约束条件,并在直角坐标系aOb内画出这个约束条件表示的平面区域;
(2)当(a, b )在(1)所得的约束条件内移动时,求△ABC面积S的最大值,并求此时(a , b)的值.(14分)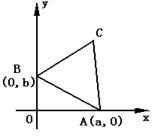
19.已知直线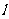 :y=k(x+2
:y=k(x+2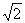 )与圆O:x2+y2=4相交于A、B两点,O是坐标原点,三角形ABO的面积为S.
)与圆O:x2+y2=4相交于A、B两点,O是坐标原点,三角形ABO的面积为S.
(1)试将S表示成k的函数,并求出它的定义域;
(2)求S的最大值,并求取得最大值时k的值.(14分)
18.已知与曲线C: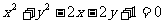 相切的直线
相切的直线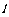 交
交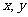 的正半轴与
的正半轴与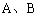 两点,O为原点,
两点,O为原点,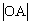 =a,
=a,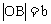 ,
,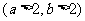 .
.
(1)求线段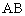 中点的轨迹方程;
中点的轨迹方程;
(2)求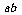 的最小值.(12分)
的最小值.(12分)
17.某承包户承包了两块鱼塘,一块准备放养鲫鱼,另一块准备放养鲤鱼,现知放养这两种鱼苗时都需要鱼料A、B、C,每千克鱼苗所需饲料量如下表:
|
鱼类 |
鱼料A |
鱼料B |
鱼料C |
|
鲫鱼/kg |
15g |
5g |
8g |
|
鲤鱼/kg |
8g |
5g |
18g |
如果这两种鱼长到成鱼时,鲫鱼和鲤鱼分别是当时放养鱼苗重量的30倍与50倍,目前这位承包户只有饲料A、B、C分别为 120g、50g、144g,问如何放养这两种鱼苗,才能使得成鱼的重量最重.(12分)
16.求经过点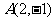 ,和直线
,和直线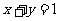 相切,且圆心在直线
相切,且圆心在直线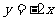 上的圆方程.(12分)
上的圆方程.(12分)
15.已知直线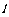 满足下列两个条件:
满足下列两个条件:
(1)过直线y = – x + 1和y = 2x + 4的交点;
(2)与直线x –3y + 2 = 0 垂直,求直线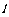 的方程.(12分)
的方程.(12分)
14.已知直线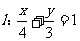 ,
,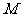 是
是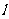 上一动点,过
上一动点,过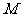 作
作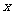 轴、
轴、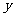 轴的垂线,垂足分别为
轴的垂线,垂足分别为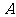 、
、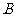 ,则在
,则在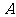 、
、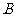 连线上,且满足
连线上,且满足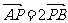 的点
的点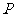 的轨迹方程是____________________.
的轨迹方程是____________________.
13.点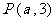 到直线
到直线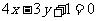 的距离等于4,且在不等式
的距离等于4,且在不等式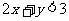 表示的平面区域内,则点
表示的平面区域内,则点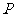 的坐标是_______________.
的坐标是_______________.
12.若实数x,y满足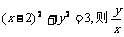 的最大值是
.
的最大值是
.
11.直线l的倾角α满足4sinα=3cosα,而且它在x轴上的截距为3,则直线l的方程是
_____________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com