
2.(本题满分10分)
已知曲线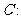
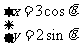 ,直线
,直线
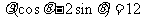 .
.
⑴将直线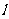 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
⑵设点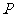 在曲线
在曲线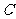 上,求
上,求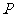 点到直线
点到直线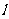 距离的最小值.
距离的最小值.
(总分40分,加试时间30分钟)
答卷前,请考生务必将自己的学校、姓名、考试号等信息填写在答卷密封线内.解答过程应写在答题卷的相应位置上,在其它地方答题无效。
1.(本题满分10分)
已知在一个二阶矩阵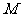 对应变换的作用下,点
对应变换的作用下,点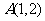 变成了点
变成了点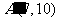 ,点
,点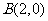 变成了点
变成了点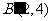 ,求矩阵
,求矩阵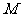 .
.
20.(本题满分16分)
已知函数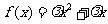 ,
,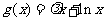 ,
,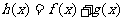 ,其中
,其中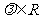 ,且
,且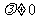 .
.
⑴当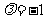 时,求函数
时,求函数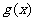 的最大值;
的最大值;
⑵求函数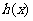 的单调区间;
的单调区间;
⑶设函数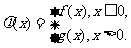 若对任意给定的非零实数
若对任意给定的非零实数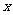 ,存在非零实数
,存在非零实数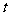 (
(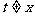 ),
),
使得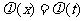 成立,求实数
成立,求实数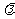 的取值范围.
的取值范围.
[扬州市教育科学研究院命制]
高三数学试卷 第4页(共4页)
扬州市2009~2010学年度第一学期期末高考模拟考试
19.(本小题满分16分)
已知数列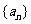 ,
,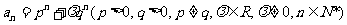 .
.
⑴求证:数列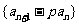 为等比数列;
为等比数列;
⑵数列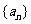 中,是否存在连续的三项,这三项构成等比数列?试说明理由;
中,是否存在连续的三项,这三项构成等比数列?试说明理由;
⑶设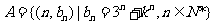 ,其中
,其中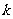 为常数,且
为常数,且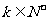 ,
,
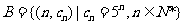 ,求
,求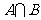 .
.
18. (本题满分15分)
 已知圆
已知圆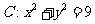 ,点
,点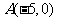 ,直线
,直线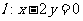 .
.
⑴求与圆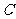 相切,且与直线
相切,且与直线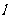 垂直的直线方程;
垂直的直线方程;
⑵在直线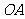 上(
上(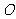 为坐标原点),存在定点
为坐标原点),存在定点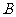 (不同于点
(不同于点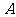 ),
),
满足:对于圆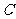 上任一点
上任一点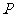 ,都有
,都有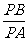 为一常数,试求所有
为一常数,试求所有
满足条件的点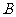 的坐标.
的坐标.
17.(本题满分15分)
扬州某地区要建造一条防洪堤,其横断面为等腰梯形,腰与底边成角为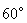 (如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为
(如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为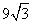 平方米,且高度不低于
平方米,且高度不低于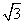 米.记防洪堤横断面的腰长为
米.记防洪堤横断面的腰长为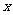 (米),外周长(梯形的上底线段
(米),外周长(梯形的上底线段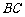 与两腰长的和)为
与两腰长的和)为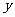 (米).
(米).
⑴求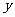 关于
关于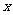 的函数关系式,并指出其定义域;
的函数关系式,并指出其定义域;
⑵要使防洪堤横断面的外周长不超过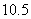 米,则其腰长
米,则其腰长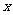 应在什么范围内?
应在什么范围内?
 ⑶当防洪堤的腰长
⑶当防洪堤的腰长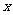 为多少米时,堤的上面与两侧面的水泥用料最省
为多少米时,堤的上面与两侧面的水泥用料最省
(即断面的外周长最小)?求此时外周长的值.
高三数学试卷 第3页(共4页)
16. (本题满分14分)
(本题满分14分)
如图,平行四边形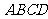 中,
中,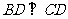 ,正方形
,正方形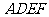 所在的
所在的
平面和平面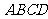 垂直,
垂直,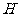 是
是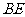 的中点,
的中点,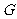 是
是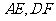 的交点.
的交点.
⑴求证: 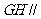 平面
平面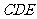 ;
;
⑵求证: 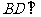 平面
平面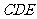 .
.
15.(本题满分14分)
 已知函数
已知函数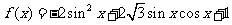
⑴求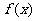 的最小正周期及对称中心;
的最小正周期及对称中心;
⑵若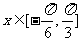 ,求
,求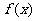 的最大值和最小值.
的最大值和最小值.
14.已知数列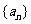 满足:
满足: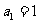 ,
,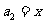 (
(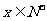 ),
), ,若前
,若前 项中
项中
恰好含有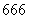 项为
项为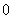 ,则
,则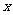 的值为 ▲ .
的值为 ▲ .
高三数学试卷 第2页(共4页)
13.若函数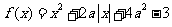 的零点有且只有一个,则实数
的零点有且只有一个,则实数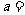 ▲ .
▲ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com