
20、(13分)已知椭圆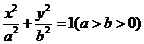 经过点
经过点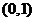 ,过右焦点F且不与x轴重合的动直线L交椭圆于
,过右焦点F且不与x轴重合的动直线L交椭圆于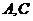 两点,当动直线L的斜率为2时,坐标原点O到L的距离为
两点,当动直线L的斜率为2时,坐标原点O到L的距离为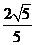 .
.
(Ⅰ) 求椭圆的方程;
(Ⅱ) 过F的另一直线交椭圆于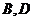 两点,且
两点,且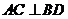 ,当四边形
,当四边形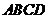 的面积S=
的面积S=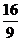 时,求直线L的方程.
时,求直线L的方程.
解:(Ⅰ)设F(c,0),则直线L的方程为2x-y-2c=0,∵坐标原点O到L的距离为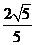 ,
,
∴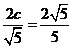 ,c=1。………………………………………………………2分
,c=1。………………………………………………………2分
∵椭圆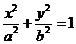 经过点
经过点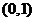 ,∴
,∴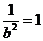 ,b=1,由
,b=1,由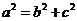 得
得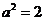 。
。
∴椭圆的方程为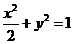 ……………………………………………4分
……………………………………………4分
(Ⅱ)由(Ⅰ)知,直线L过点F(1,0),设其方程为y=k(x-1)(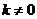 ),点A(
),点A(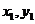 ),C(
),C(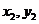 ),
),
解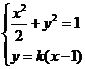 得,
得,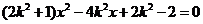 。
。
∴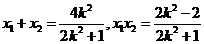 ,……………………………………………6分
,……………………………………………6分
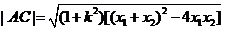 =
=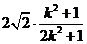
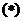 ……………………………8分
……………………………8分
∵过F的另一直线交椭圆于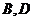 两点,且
两点,且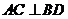 ,
, 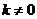 ,
,
∴直线BD的方程为y=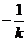 (x-1) 。
(x-1) 。
把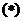 式中k换成
式中k换成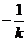 ,类比可得
,类比可得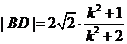 ,…………………………10分
,…………………………10分
∴四边形 的面积
的面积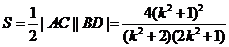
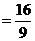 , …………11分
, …………11分
解得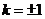 , ∴直线L的方程为x-y-1=0或x+y-1=0
。 ………………………13分
, ∴直线L的方程为x-y-1=0或x+y-1=0
。 ………………………13分
19、(14分)已知函数f(x)=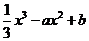 在x=-2处有极值.
在x=-2处有极值.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若函数f(x)在区间[-3,3]上有且仅有一个零点,求b的取值范围。
解: (Ⅰ)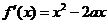 …………………………………………1分
…………………………………………1分
由题意知: 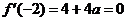 ,得a=-1,………………………2分
,得a=-1,………………………2分
∴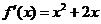 ,
,
令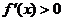 ,得x<-2或x>0, ………………………4分
,得x<-2或x>0, ………………………4分
令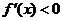 ,得-2<x<0, ………………………5分
,得-2<x<0, ………………………5分
∴f(x)的单调递增区间是(-¥,-2)和(0,+¥),
单调递减区间是(-2,0)。…………………………………………6分
(Ⅱ)由(Ⅰ)知,f(x)= 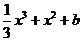 ,
,
f(-2)=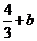 为函数f(x)极大值,f(0)=b为极小值。…………………8分
为函数f(x)极大值,f(0)=b为极小值。…………………8分
∵函数f(x)在区间[-3,3]上有且仅有一个零点,
∴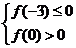 或
或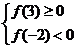 或
或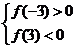 或
或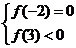 或
或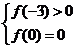 ,
,
即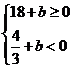 ,…………………………………………………………13分
,…………………………………………………………13分
∴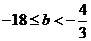 ,即b的取值范围是
,即b的取值范围是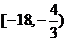 。 …………………14分
。 …………………14分
18、(14分)已知数列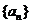 的前n项和为
的前n项和为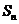 ,
,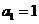 ,
,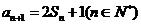 ,等差数列
,等差数列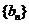 中,
中,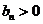
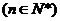 ,且
,且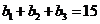 ,又
,又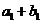 、
、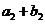 、
、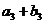 成等比数列.
成等比数列.
(Ⅰ)求数列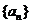 、
、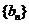 的通项公式;
的通项公式;
(Ⅱ)求数列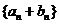 的前n项和Tn.
的前n项和Tn.
解:(Ⅰ)∵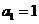 ,
,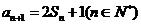 ,
,
∴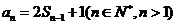 ,
,
∴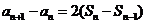 ,
,
∴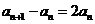 ,
,
∴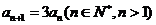 …………………………3分
…………………………3分
而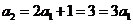 ,∴
,∴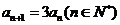
∴数列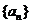 是以1为首项,3为公比的等比数列,
是以1为首项,3为公比的等比数列,
∴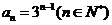 …………………………5分
…………………………5分
∴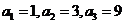 ,
,
在等差数列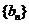 中,∵
中,∵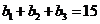 ,∴
,∴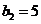 。
。
又因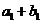 、
、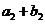 、
、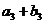 成等比数列,设等差数列
成等比数列,设等差数列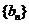 的公差为d,
的公差为d,
∴(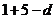 )
)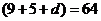 ………………………………7分
………………………………7分
解得d=-10,或d=2, ∵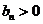
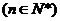 ,∴舍去d=-10,取d=2, ∴b1=3,
,∴舍去d=-10,取d=2, ∴b1=3,
∴bn=2n+1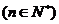 ,
………………………………9分
,
………………………………9分
(Ⅱ)由(Ⅰ)知
∴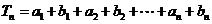
=(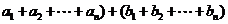
=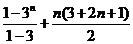
=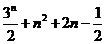 ………………………………14分
………………………………14分
17、(14分)设集合P={1,2,3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为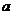 和
和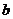 组成数对(
组成数对(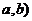 ,并构成函数
,并构成函数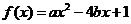 .
.
(Ⅰ)写出所有可能的数对(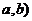 ,并计算
,并计算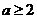 ,且
,且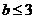 的概率;
的概率;
(Ⅱ)求函数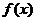 在区间[
在区间[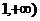 上是增函数的概率.
上是增函数的概率.
解: (Ⅰ)所有基本事件如下:
(1,-1),(1,1),(1,2),(1,3),(1,4),
(2,-1),(2,1),(2,2),(2,3),(2,4),
(3,-1),(3,1),(3,2),(3,3),(3,4) ,共有15个。………………………………4分
设事件“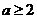 ,且
,且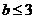 ”为A,
”为A,
则事件A包含的基本事件有8个, ………………………………… 6分
所以P(A)=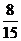 。
……………………………………………8分
。
……………………………………………8分
(Ⅱ)设事件“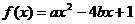 在区间
在区间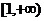 上为增函数”为B,
上为增函数”为B,
因函数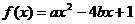 的图象的对称轴为
的图象的对称轴为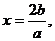 且
且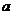 >0,
>0,
所以要使事件B发生,只需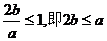 。…………………………10分
。…………………………10分
由满足题意的数对有(1,-1)、(2,-1)、(2,1)、(3,-1)、(3,1),共5个,
…………………………12分
所以,P(B)= 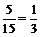 .
…………………………14分
.
…………………………14分
16、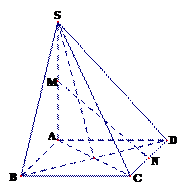 (13分)如图,在四棱锥
(13分)如图,在四棱锥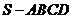 中,底面
中,底面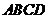 是菱形,
是菱形,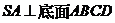 ,
,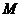 为
为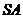 的中点,
的中点,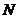 为
为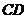 的中点.
的中点.
(Ⅰ)证明:平面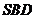
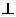 平面
平面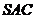 ;
;
(Ⅱ)证明:直线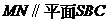 .
.
证明:(Ⅰ)∵ABCD是菱形,
∴BD^AC, ………………………………1分
∵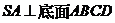 ,∴BD^SA, ……………2分
,∴BD^SA, ……………2分
∵SA与AC交于A,
∴BD^平面SAC, …………………………………4分
∵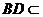 平面
平面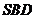
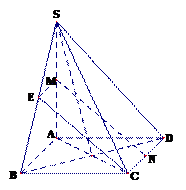 ∴平面
∴平面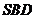
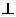 平面
平面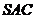 …………………6分
…………………6分
(Ⅱ)取SB中点E,连接ME,CE,
∵M为SA中点,∴ME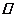 AB且ME=
AB且ME=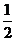 AB, ………8分
AB, ………8分
又∵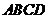 是菱形,N为
是菱形,N为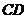 的中点,
的中点,
∴CN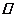 AB且CN=
AB且CN=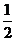 CD=
CD=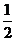 AB, …………………10分
AB, …………………10分
∴CN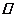 EM,且CN=EM,
EM,且CN=EM,
∴四边形CNME是平行四边形,
∴MN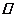 CE,
…………………12分
CE,
…………………12分
又MNË平面SBC, CEÌ平面SBC,
∴直线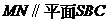 …………………13分
…………………13分
15、 (12分)已知函数f(x)=
(12分)已知函数f(x)=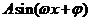 (其中A>0,
(其中A>0,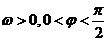 )的图象如图所示。
)的图象如图所示。
(Ⅰ)求A,w及j的值;
(Ⅱ)若tana=2,求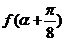 的值。
的值。
解:(Ⅰ)由图知A=2, ……………………1分
T=2(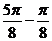 )=p,
)=p,
∴w=2, ……………………3分
∴f(x)=2sin(2x+j)
又∵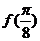 =2sin(
=2sin(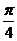 +j)=2,
+j)=2,
∴sin(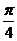 +j)=1,
+j)=1,
∴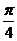 +j=
+j=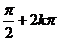 ,j=
,j=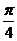 +
+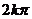 ,(kÎZ)
,(kÎZ)
∵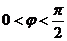 ,∴j=
,∴j=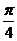 ……………………6分
……………………6分
由(Ⅰ)知:f(x)=2sin(2x+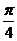 ),
),
∴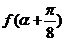 =2sin(2a+
=2sin(2a+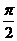 )=2cos2a=4cos2a-2…………9分
)=2cos2a=4cos2a-2…………9分
∵tana=2, ∴sina=2cosa,
又∵sin2a+cos2a=1, ∴cos2a=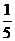 ,
,
∴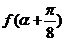 =
=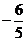 ……………………12分
……………………12分
9、1 ; 10、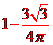 ;
11、x-2y-2=0 ; 12、
;
11、x-2y-2=0 ; 12、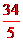 ;
13、6 ; 14、 [-2,0]。
;
13、6 ; 14、 [-2,0]。
20、(13分)已知椭圆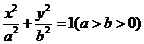 经过点
经过点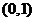 ,过右焦点F且不与x轴重合的动直线L交椭圆于
,过右焦点F且不与x轴重合的动直线L交椭圆于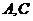 两点,当动直线L的斜率为2时,坐标原点O到L的距离为
两点,当动直线L的斜率为2时,坐标原点O到L的距离为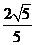 .
.
(Ⅰ) 求椭圆的方程;
(Ⅱ) 过F的另一直线交椭圆于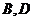 两点,且
两点,且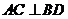 ,当四边形
,当四边形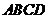 的面积S=
的面积S=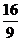 时,求直线L的方程.
时,求直线L的方程.
丰台区2010年高三统一练习(二)
数学(文科)
19、(14分)已知函数f(x)=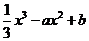 在x=-2处有极值.
在x=-2处有极值.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若函数f(x)在区间[-3,3]上有且仅有一个零点,求b的取值范围.
18、(14分)已知数列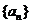 的前n项和为
的前n项和为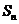 ,
,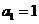 ,
,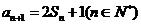 ,等差数列
,等差数列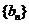 中
中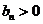
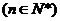 ,且
,且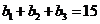 ,又
,又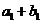 、
、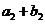 、
、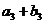 成等比数列.
成等比数列.
(Ⅰ)求数列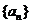 、
、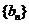 的通项公式;
的通项公式;
(Ⅱ)求数列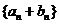 的前n项和Tn.
的前n项和Tn.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com