
3.设 是夹角为
是夹角为 的单位向量,若
的单位向量,若 是单位向量,则
是单位向量,则 的取值范围是_ ▲__
的取值范围是_ ▲__
2.设复数 ,则
,则 等于_ _▲____.
等于_ _▲____.
1. 设集合 ,若
,若 ,则
,则 与
与 的关系是_ _▲___ (填
的关系是_ _▲___ (填 、
、 、
、 、
、 )
)
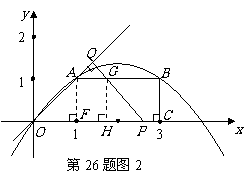
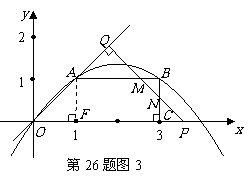
090](1)解:把A( ,0),C(3,
,0),C(3, )代入抛物线
)代入抛物线  得
得
 ················································································· 1分
················································································· 1分
整理得  ··············· ………………
2分 解得
··············· ………………
2分 解得 ………………3分
………………3分
∴抛物线的解析式为
 ··································································· 4分
··································································· 4分
(2)令 解得
解得 
∴ B点坐标为(4,0)
又∵D点坐标为(0, ) ∴AB∥CD ∴四边形ABCD是梯形.
) ∴AB∥CD ∴四边形ABCD是梯形.
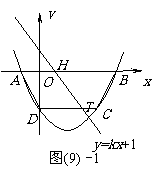 ∴S梯形ABCD =
∴S梯形ABCD = ···························· 5分
···························· 5分
设直线 与x轴的交点为H,
与x轴的交点为H,
与CD的交点为T,
则H( ,0), T(
,0), T( ,
, )··················· 6分
)··················· 6分
∵直线 将四边形ABCD面积二等分
将四边形ABCD面积二等分
∴S梯形AHTD = S梯形ABCD=4
S梯形ABCD=4
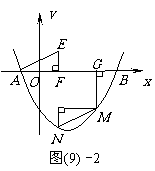 ∴
∴ ····································· 7分
····································· 7分
∴ ···························································· 8分
···························································· 8分
(3)∵MG⊥ 轴于点G,线段MG︰AG=1︰2
轴于点G,线段MG︰AG=1︰2
∴设M(m, ),········································ 9分
),········································ 9分
∵点M在抛物线上 ∴
解得 (舍去) ···························· 10分
(舍去) ···························· 10分
∴M点坐标为(3, )····················································································· 11分
)····················································································· 11分
根据中心对称图形性质知,MQ∥AF,MQ=AF,NQ=EF,
∴N点坐标为(1, ) ···················································································· 12分
) ···················································································· 12分
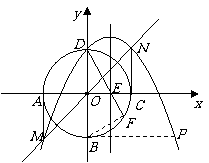
089]解:(1) 圆心
圆心 在坐标原点,圆
在坐标原点,圆 的半径为1,
的半径为1,
 点
点 的坐标分别为
的坐标分别为
 抛物线与直线
抛物线与直线 交于点
交于点 ,且
,且 分别与圆
分别与圆 相切于点
相切于点 和点
和点 ,
,

 .······························································································· 2分
.······························································································· 2分
 点
点 在抛物线上,将
在抛物线上,将 的坐标代入
的坐标代入
 ,得:
,得: 解之,得:
解之,得:
 抛物线的解析式为:
抛物线的解析式为: .······································································ 4分
.······································································ 4分
(2)
 抛物线的对称轴为
抛物线的对称轴为 ,
,
 .···················· 6分
.···················· 6分
连结 ,
,
 ,
, ,
,
又 ,
,
 ,
,
 .····································································· 8分
.····································································· 8分
(3)点 在抛物线上.································································································ 9分
在抛物线上.································································································ 9分
设过 点的直线为:
点的直线为: ,
,
将点 的坐标代入
的坐标代入 ,得:
,得: ,
,
 直线
直线 为:
为: .······················································································ 10分
.······················································································ 10分
过点 作圆
作圆 的切线
的切线 与
与 轴平行,
轴平行, 点的纵坐标为
点的纵坐标为 ,
,
将 代入
代入 ,得:
,得: .
.

 点的坐标为
点的坐标为 ,··························································································· 11分
,··························································································· 11分
当 时,
时, ,
,
所以, 点在抛物线
点在抛物线 上.···································································· 12分
上.···································································· 12分
说明:解答题各小题中只给出了1种解法,其它解法只要步骤合理、解答正确均应得到相应的分数.
088]解:(1)法一:由图象可知:抛物线经过原点,
设抛物线解析式为 .
.
把 ,
, 代入上式得:···················································································· 1分
代入上式得:···················································································· 1分
 解得
解得 ······················································································· 3分
······················································································· 3分
∴所求抛物线解析式为 ········································································ 4分
········································································ 4分
法二:∵ ,
, ,
,
∴抛物线的对称轴是直线 .
.
设抛物线解析式为 (
( )······························································ 1分
)······························································ 1分
把 ,
, 代入得
代入得
 解得
解得 ··········································································· 3分
··········································································· 3分
∴所求抛物线解析式为 .····························································· 4分
.····························································· 4分
(2)分三种情况:
①当 ,重叠部分的面积是
,重叠部分的面积是 ,过点
,过点 作
作 轴于点
轴于点 ,
,
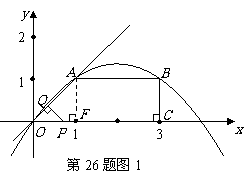 ∵
∵ ,在
,在 中,
中, ,
, ,
,
在 中,
中, ,
, ,
,
∴ ,
,
 ∴
∴ .··············································· 6分
.··············································· 6分
②当 ,设
,设 交
交 于点
于点 ,作
,作 轴于点
轴于点 ,
,
 ,则四边形
,则四边形 是等腰梯形,
是等腰梯形,
重叠部分的面积是 .
.
∴ ,
,
∴ .··········· 8分
.··········· 8分
③当 ,设
,设 与
与 交于点
交于点 ,交
,交 于点
于点 ,重叠部分的面积是
,重叠部分的面积是 .
.
 因为
因为 和
和 都是等腰直角三角形,所以重叠部分的面积是
都是等腰直角三角形,所以重叠部分的面积是
 .
.
∵ ,
, ,
,
∴ ,
,
∴ ,
,
∴
 .················································ 10分
.················································ 10分
(3)存在  ···································································································· 12分
···································································································· 12分
 ··································································································· 14分
··································································································· 14分
087](天门)略
086]⑴证明:∵BC是⊙O的直径
∴∠BAC=90o
又∵EM⊥BC,BM平分∠ABC,
∴AM=ME,∠AMN=EMN
又∵MN=MN,
∴△ANM≌△ENM
⑵∵AB2=AF·AC
∴
又∵∠BAC=∠FAB=90o
∴△ABF∽△ACB
∴∠ABF=∠C
又∵∠FBC=∠ABC+∠FBA=90o
∴FB是⊙O的切线
⑶由⑴得AN=EN,AM=EM,∠AMN=EMN,
又∵AN∥ME,∴∠ANM=∠EMN,
∴∠AMN=∠ANM,∴AN=AM,
∴AM=ME=EN=AN
∴四边形AMEN是菱形
∵cos∠ABD= ,∠ADB=90o
,∠ADB=90o
∴
设BD=3x,则AB=5x,,由勾股定理
而AD=12,∴x=3
∴BD=9,AB=15
∵MB平分∠AME,∴BE=AB=15
∴DE=BE-BD=6
∵ND∥ME,∴∠BND=∠BME,又∵∠NBD=∠MBE
∴△BND∽△BME,则
设ME=x,则ND=12-x, ,解得x=
,解得x=
∴S=ME·DE= ×6=45
×6=45
085]解: (1)由题知:  ……………………………………1 分
……………………………………1 分
解得:  ……………………………………………………………2分
……………………………………………………………2分
∴ 所求抛物线解析式为:  ……………………………3分
……………………………3分
(2) 存在符合条件的点P, 其坐标为P (-1,  )或P(-1,-
)或P(-1,-  )
)
或P (-1, 6) 或P (-1,  )………………………………………………………7分
)………………………………………………………7分
(3)解法①:
过点E 作EF⊥x 轴于点F , 设E ( a ,- -2a+3 )( -3< a < 0 )
-2a+3 )( -3< a < 0 )
∴EF=- -2a+3,BF=a+3,OF=-a ………………………………………………8
分
-2a+3,BF=a+3,OF=-a ………………………………………………8
分
∴S四边形BOCE
=  BF·EF +
BF·EF +  (OC +EF)·OF
(OC +EF)·OF
= ( a+3 )·(-
( a+3 )·(- -2a+3) +
-2a+3) +  (-
(- -2a+6)·(-a)……………………………9 分
-2a+6)·(-a)……………………………9 分
= ………………………………………………………………………10 分
………………………………………………………………………10 分
=-
 +
+
∴ 当a =- 时,S四边形BOCE 最大, 且最大值为
时,S四边形BOCE 最大, 且最大值为  .……………………………11
分
.……………………………11
分
此时,点E 坐标为 (- ,
, )……………………………………………………12分
)……………………………………………………12分
解法②:
过点E 作EF⊥x 轴于点F, 设E ( x , y ) ( -3< x < 0 ) …………………………8分
则S四边形BOCE
=  (3 + y )·(-x) +
(3 + y )·(-x) +  ( 3 + x )·y ………………………………………9分
( 3 + x )·y ………………………………………9分
=  ( y-x)=
( y-x)=  (
( ) …………………………………10
分
) …………………………………10
分
= -
 +
+ 
∴ 当x =- 时,S四边形BOCE 最大,且最大值为
时,S四边形BOCE 最大,且最大值为  . …………………………11分
. …………………………11分
此时,点E 坐标为 (- ,
, ) ……………………………………………………12分
) ……………………………………………………12分
084]解:(1)⊙P与x轴相切.
∵直线y=-2x-8与x轴交于A(4,0),与y轴交于B(0,-8),
∴OA=4,OB=8.由题意,OP=-k,∴PB=PA=8+k.
在Rt△AOP中,k2+42=(8+k)2,
∴k=-3,∴OP等于⊙P的半径,
∴⊙P与x轴相切.
(2)设⊙P与直线l交于C,D两点,连结PC,PD当圆心P在线段OB上时,作PE⊥CD于E.
 ∵△PCD为正三角形,∴DE=
∵△PCD为正三角形,∴DE= CD=
CD= ,PD=3,
,PD=3,
∴PE= .
.
∵∠AOB=∠PEB=90°, ∠ABO=∠PBE,
∴△AOB∽△PEB,
∴
 ,
,
∴ ∴
∴ ,
,
∴ ,∴
,∴ .
.
当圆心P在线段OB延长线上时,同理可得P(0,- -8),
-8),
∴k=- -8,∴当k=
-8,∴当k= -8或k=-
-8或k=- -8时,以⊙P与直线l的两个交点和圆心P为顶点的三角形是正三角形.
-8时,以⊙P与直线l的两个交点和圆心P为顶点的三角形是正三角形.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com