
1.请分别从内容、结构和语言三方面分析本文使用的三节诗句的作用。(6分)
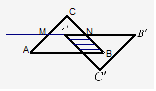
040](1)解 ①如图1,当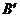 在△ABC内时,重叠部分是平行四边形,由题意得:
在△ABC内时,重叠部分是平行四边形,由题意得:
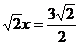 解得x=
解得x=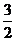 ……(2分)
……(2分)
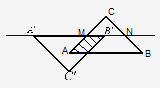
②如图3 ,当
,当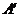 在△ABC内时,重叠部分是平行四边形,由题意得:
在△ABC内时,重叠部分是平行四边形,由题意得:
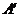 N=
N=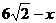 列式得(
列式得(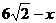 )×
)×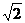 =
=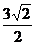
解得x=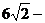
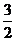 ……(2分)
……(2分)
 综上所述,当△
综上所述,当△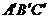 与△
与△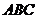 重叠部分面积 为
重叠部分面积 为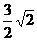 平方厘米时,△
平方厘米时,△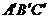 移动的时间为
移动的时间为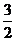 或(
或(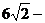
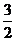 )秒。
)秒。
|
|
|
|||||||
|
(2)
①如图1,当0≤x≤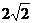 时
时 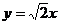 ……(1分)
……(1分)
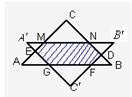
②如图2,当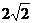 ≤x≤
≤x≤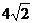 时,如图,△D
时,如图,△D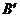 N, △
N, △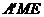 ,△
,△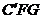 是等腰直角三角形,
是等腰直角三角形, 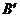 N=
N=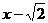 ,GF=MN=
,GF=MN=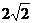 ,
,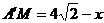
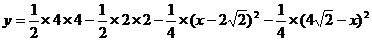
即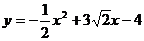 …(3分)
…(3分)
③如图3,当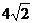 ≤x≤
≤x≤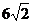 时,
时,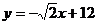 …(1分)
…(1分)
(3)①当0≤x≤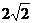 时,
时, 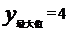 ……(1分)
……(1分)
②当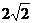 ≤x≤
≤x≤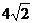 时,
时, 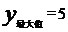 ……(2分)
……(2分)
③当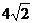 ≤x≤
≤x≤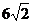 时,
时, 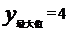 ……(1分)
……(1分)
所以,△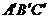 与△
与△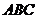 重叠部分面积的最大值为5。
重叠部分面积的最大值为5。
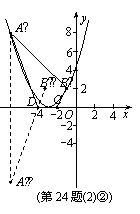
039](1) 将点A(-4,8)的坐标代入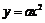 ,解得
,解得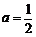 . ……1分
. ……1分
将点B(2,n)的坐标代入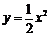 ,求得点B的坐标为(2,2),
,求得点B的坐标为(2,2),
则点B关于x轴对称点P的坐标为(2,-2). ……1分
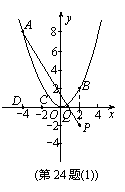 直线AP的解析式是
直线AP的解析式是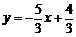 .
……1分
.
……1分
令y=0,得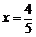 .即所求点Q的坐标是(
.即所求点Q的坐标是(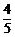 ,0). ……1分
,0). ……1分
(2)① 解法1:CQ=︱-2-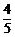 ︱=
︱=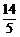 , ……1分
, ……1分
故将抛物线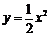 向左平移
向左平移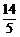 个单位时,A′C+CB′最短,
个单位时,A′C+CB′最短,
此时抛物线的函数解析式为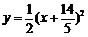 . ……1分
. ……1分
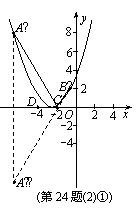 解法2:设将抛物线
解法2:设将抛物线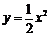 向左平移m个单位,则平移后A′,B′的坐标分别为A′(-4-m,8)和B′(2-m,2),点A′关于x轴对称点的
向左平移m个单位,则平移后A′,B′的坐标分别为A′(-4-m,8)和B′(2-m,2),点A′关于x轴对称点的 坐标为A′′(-4-m,-8).
坐标为A′′(-4-m,-8).
直线A′′B′的解析式为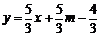 . 要使A′C+CB′最短,点C应在直
. 要使A′C+CB′最短,点C应在直 线A′′B′上,将点C(-2,0)代入直线A′′B′的解析式,解得
线A′′B′上,将点C(-2,0)代入直线A′′B′的解析式,解得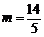 .
.
故将抛物线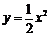 向左平移
向左平移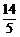 个单位时A′C+CB′最短,此时抛物线的函数解析式为
个单位时A′C+CB′最短,此时抛物线的函数解析式为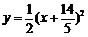 . ……1分
. ……1分
 ② 左右平移抛物线
② 左右平移抛物线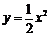 ,因为线段A′B′和CD的长是定值,所以要使四边形A′B′CD的周长最短,只要使A′D+CB′最短;
……1分
,因为线段A′B′和CD的长是定值,所以要使四边形A′B′CD的周长最短,只要使A′D+CB′最短;
……1分
第一种情况:如果将抛物线向右平移,显然有A′D+CB′>AD+CB,因此不存在某个位置,使四边形A′B′CD的周长最短.……1分
第二种情况:设抛物线向左平移了b个单位,则点A′和点B′的坐标分别为A′(-4-b,8)和B′(2-b,2).
因为CD=2,因此将点B′向左平移2个单位得B′′(-b,2),
要使A′D+CB′最短,只要使A′D+DB′′最短. ……1分
点A′关于x轴对称点的坐标为A′′(-4-b,-8),直线A′′B′′的解析式为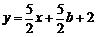 .要使A′D+DB′′最短,点D应在直线A′′B′′上,将点D(-4,0)代入直线A′′B′′的解析式,解得
.要使A′D+DB′′最短,点D应在直线A′′B′′上,将点D(-4,0)代入直线A′′B′′的解析式,解得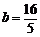 .故将抛物线向左平移时,存在某个位置,使四边形A′B′CD的周长最短,此时抛物线的函数解析式为
.故将抛物线向左平移时,存在某个位置,使四边形A′B′CD的周长最短,此时抛物线的函数解析式为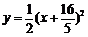 .……1分
.……1分
038]解:(1)矩形(长方形);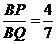 .
.
(2)①
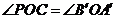 ,
,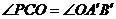
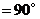 ,
,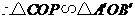 .
.
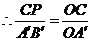 ,即
,即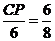 ,
,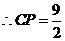 ,
,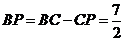 .································ 4分
.································ 4分
同理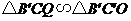 ,
,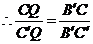 ,
, 即
即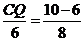 ,
,
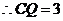 ,
,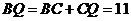 .
.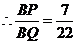 .······················································· 6分
.······················································· 6分
②在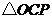 和
和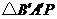 中,
中,
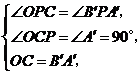 [来源:ZXXK]
[来源:ZXXK]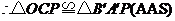 .··············································· 7分
.··············································· 7分
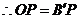 .设
.设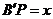 ,在
,在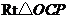 中,
中, 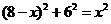 ,解得
,解得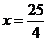 .·· 8分
.·· 8分
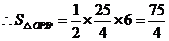 .······················································································· 9分
.······················································································· 9分
(3)存在这样的点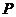 和点
和点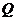 ,使
,使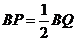 .························································· 10分
.························································· 10分
 点
点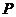 的坐标是
的坐标是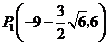 ,
,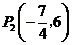 .·························································· 12分
.·························································· 12分
对于第(3)题,我们提供如下详细解答,对学生无此要求.
过点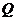 画
画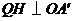 于
于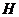 ,连结
,连结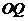 ,则
,则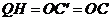 ,
,
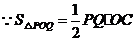 ,
,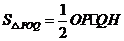 ,
,
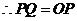 .设
.设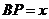 ,
,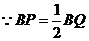 ,
,
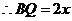 ,
,
① 如图1,当点P在点B左侧时,
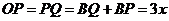 ,
,
在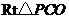 中,
中,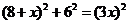 ,
,
解得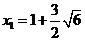 ,
,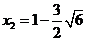 (不符实际,舍去).
(不符实际,舍去).
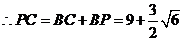 ,
,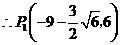 .
.
②如图2 ,当点P在点B右侧时,
,当点P在点B右侧时,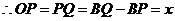 ,
,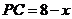 .
.
在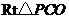 中,
中,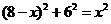 ,解得
,解得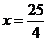 .
.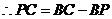
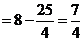 ,
,
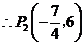 .综上可知,存在点
.综上可知,存在点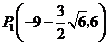 ,
,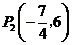 ,使
,使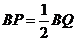 .
.
037]解:(1)设第一象限内的点B(m,n),则tan∠POB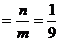 ,得m=9n,又点B在函数
,得m=9n,又点B在函数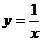 的图象上,得
的图象上,得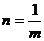 ,所以m=3(-3舍去),点B为
,所以m=3(-3舍去),点B为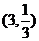 ,
,
而AB∥x轴,所以点A(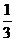 ,
,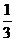 ),所以
),所以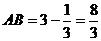 ;
;
(2)由条件可知所求抛物线开口向下,设点A(a , a),B(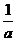 ,a),则AB=
,a),则AB=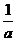 -
a =
-
a = 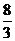 ,
,
所以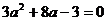 ,解得
,解得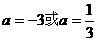 .
.
当a = -3时,点A(―3,―3),B(―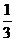 ,―3),因为顶点在y = x上,所以顶点为(-
,―3),因为顶点在y = x上,所以顶点为(-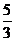 ,-
,-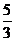 ),所以可设二次函数为
),所以可设二次函数为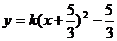 ,点A代入,解得k= -
,点A代入,解得k= -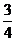 ,所以所求函数解析式为
,所以所求函数解析式为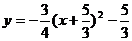 .
.
同理,当a = 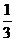 时,所求函数解析式为
时,所求函数解析式为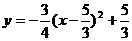 ;
;
(3)设A(a , a),B(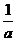 ,a),由条件可知抛物线的对称轴为
,a),由条件可知抛物线的对称轴为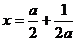 .
.
设所求二次函数解析式为: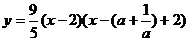 .
.
点A(a , a)代入,解得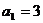 ,
,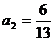 ,所以点P到直线AB的距离为3或
,所以点P到直线AB的距离为3或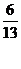 。
。
036]解:(1)由已知,得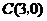 ,
,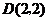 ,
,
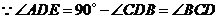 ,
,
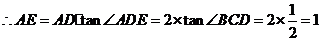 .
.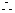
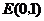 .························ (1分)
.························ (1分)
设过点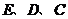 的抛物线的解析式为
的抛物线的解析式为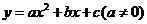 .将点
.将点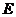 的坐标代入,得
的坐标代入,得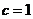 .[来源:学&将
.[来源:学&将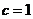 和点
和点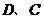 的坐标分别代入,得
的坐标分别代入,得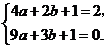 ··········································································· (2分)
··········································································· (2分)
解这个方程组, 得
得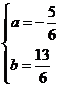 [来源:学#科#网]故抛物线的解析式为
[来源:学#科#网]故抛物线的解析式为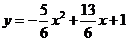 .············ (3分)
.············ (3分)
(2)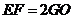 成立.························································································· (4分)
成立.························································································· (4分)
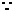 点
点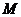 在该抛物线上,且它的横坐标为
在该抛物线上,且它的横坐标为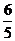 ,
,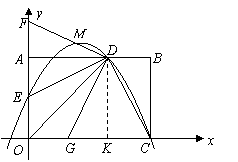
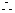 点
点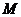 的纵坐标为
的纵坐标为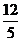 .··················· (5分)
.··················· (5分)
设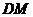 的解析式为
的解析式为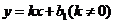 ,
,
将点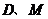 的坐标分别代入,得
的坐标分别代入,得
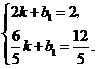 解得
解得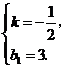
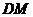 的解析式为
的解析式为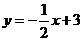 .
.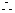
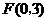 ,
,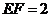 .····································· (7分)
.····································· (7分)
过点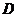 作
作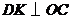 于点
于点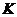 ,则
,则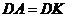 .
.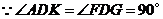 ,
,
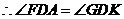 .又
.又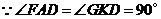 ,
,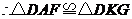 .
.
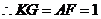 .[来
.[来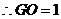 .
.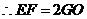 .
.
(3) 点
点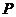 在
在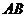 上,
上,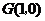 ,
,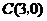 ,则设
,则设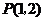 .
.
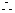
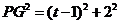 ,
,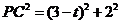 ,
,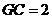 .
.
①若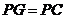 ,则
,则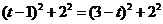 ,
,
解得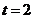 .
.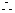
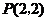 ,此时点
,此时点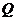 与点
与点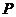 重合.
重合.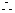
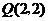 .
.
②若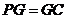 ,则
,则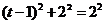 ,解得
,解得
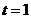 ,
,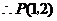 ,此时
,此时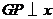 轴.
轴.
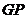 与该抛物线在第一象限内的交点
与该抛物线在第一象限内的交点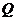 的横坐标为1,
的横坐标为1,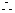 点
点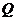 的纵坐标为
的纵坐标为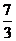 .
.
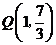 .
.
③若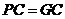 ,则
,则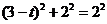 ,[来
,[来
解得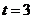 ,
,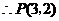 ,此时
,此时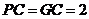 ,
,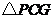 是等腰直角三角形.
是等腰直角三角形.
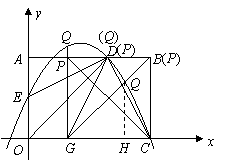
过点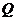 作
作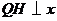 轴于点
轴于点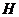 ,则
,则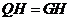 ,设
,设 ,
,
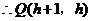 .
.
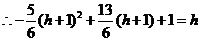 .
.
解得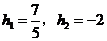 (舍去).
(舍去).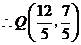 .(12分)
.(12分)
综上所述,存在三个满足条件的点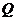 ,即
,即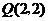 或
或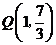 或
或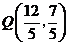 .
.
035]解:(1)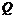 (1,0)························································································· 1分
(1,0)························································································· 1分
点P运动速度每秒钟1个单位长度.··········································································· 2分
(2) 过点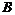 作BF⊥y轴于点
作BF⊥y轴于点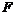 ,
,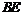 ⊥
⊥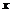 轴于点
轴于点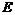 ,则
,则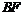 =8,
=8,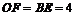 .
.
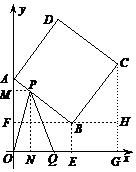 ∴
∴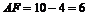 .
.
在Rt△AFB中,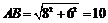 3分
3分
过点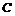 作
作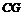 ⊥
⊥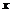 轴于点
轴于点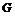 ,与
,与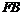 的延长线交于点
的延长线交于点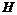 .
.
∵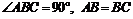 ∴△ABF≌△BCH.
∴△ABF≌△BCH.
∴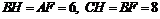 .
.
∴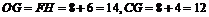 .
.
∴所求C点的坐标为(14,12). 4分
(3) 过点P作PM⊥y轴于点M,PN⊥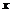 轴于点N,
轴于点N,
则△APM∽△ABF.
∴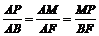 .
.
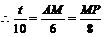 .
.
∴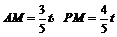 .
∴
.
∴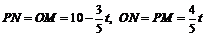 .
.
设△OPQ的面积为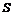 (平方单位)
(平方单位)
∴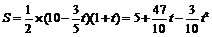 (0≤
(0≤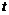 ≤10) ························································ 5分
≤10) ························································ 5分
说明:未注明自变量的取值范围不扣分.
∵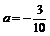 <0 ∴当
<0 ∴当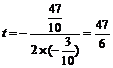 时, △OPQ的面积最大.······························ 6分
时, △OPQ的面积最大.······························ 6分
此时P的坐标为(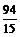 ,
,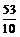 ) .················································································· 7分
) .················································································· 7分
(4) 当 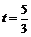 或
或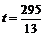 时,
OP与PQ相等.························································· 9分
时,
OP与PQ相等.························································· 9分
对一个加1分,不需写求解过程.
034]解:(1)2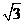 . ……………2分
. ……………2分
 (2)证明:在
(2)证明:在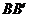 上取点
上取点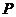 ,使
,使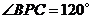 ,
,
连结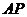 ,再在
,再在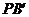 上截取
上截取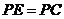 ,连结
,连结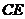 .
.
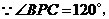
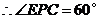 ,
,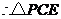 为正三角形,
为正三角形,
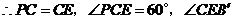 =
=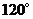 ,
,
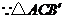 为正三角形,
为正三角形,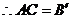
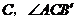 =
=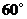 ,
,
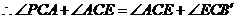 =
=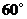 ,
,
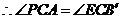 ′,
′,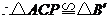
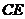 .
.
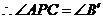
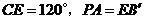 ,
,
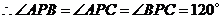 ,
,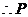 为
为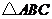 的费马点,
的费马点,
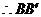 过
过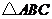 的费马点
的费马点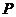 ,且
,且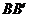 =
=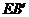 +
+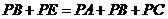 .………2分
.………2分
033]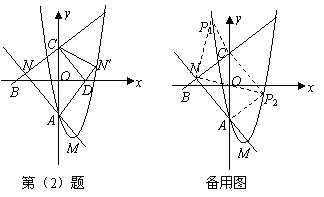
(1)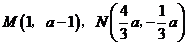 .……………4分
.……………4分
(2)由题意得点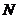 与点
与点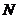 ′关于
′关于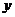 轴对称,
轴对称,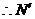
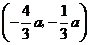 ,
,
将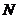 ′的坐标代入
′的坐标代入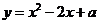 得
得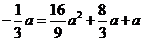 ,
,
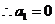 (不合题意,舍去),
(不合题意,舍去),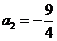 .……………2分
.……………2分
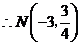 ,
, 点
点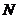 到
到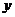 轴的距离为3.
轴的距离为3.
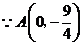 ,
,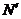
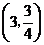 ,
, 直线
直线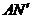 的解析式为
的解析式为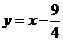 ,
,
它与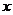 轴的交点为
轴的交点为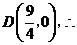 点
点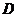 到
到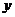 轴的距离为
轴的距离为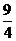 .
.
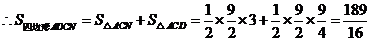 .……………2分
.……………2分
(3)当点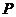 在
在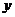 轴的左侧时,若
轴的左侧时,若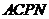 是平行四边形,则
是平行四边形,则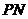 平行且等于
平行且等于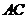 ,
,
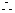 把
把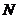 向上平移
向上平移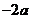 个单位得到
个单位得到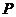 ,坐标为
,坐标为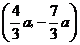 ,代入抛物线的解析式,
,代入抛物线的解析式,
得: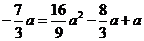
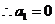 (不舍题意,舍去),
(不舍题意,舍去),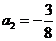 ,
,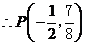 .……………2分
.……………2分
当点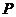 在
在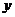 轴的右侧时,若
轴的右侧时,若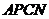 是平行四边形,则
是平行四边形,则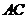 与
与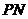 互相平分,
互相平分,
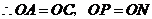 .
.
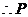 与
与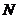 关于原点对称,
关于原点对称,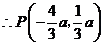 ,
,
将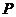 点坐标代入抛物线解析式得:
点坐标代入抛物线解析式得: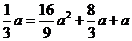 ,
,
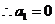 (不合题意,舍去),
(不合题意,舍去),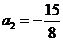 ,
,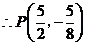 .……………2分
.……………2分
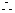 存在这样的点
存在这样的点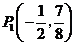 或
或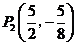 ,能使得以
,能使得以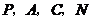 为顶点的四边形是平行四边形.
为顶点的四边形是平行四边形.
032]解:(1)在△ABC中,∵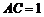 ,
,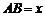 ,
,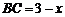 .
.
∴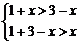 ,解得
,解得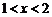 . ··············································································· 4分
. ··············································································· 4分
(2)①若AC为斜边,则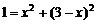 ,即
,即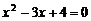 ,无解.
,无解.
②若AB为斜边,则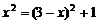 ,解得
,解得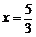 ,满足
,满足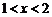 .
.
③若BC为斜边,则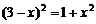 ,解得
,解得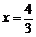 ,满足
,满足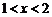 .
.
 ∴
∴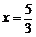 或
或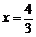 . ····································································································· 9分
. ····································································································· 9分
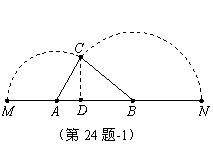
(3)在△ABC中,作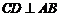 于D,
于D,
设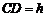 ,△ABC的面积为S,则
,△ABC的面积为S,则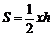 .
.
①若点D在线段AB上,
则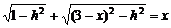 .
.
∴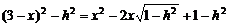 ,即
,即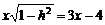 .
.
∴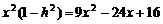 ,即
,即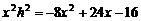 .
.
∴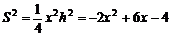
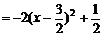 (
(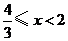 ). ······························ 11分
). ······························ 11分
当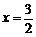 时(满足
时(满足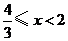 ),
),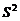 取最大值
取最大值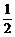 ,从而S取最大值
,从而S取最大值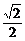 .······················ 13分
.······················ 13分
②若点D在线段MA上,
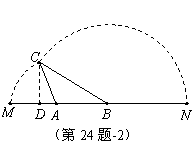 则
则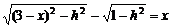 .
.
同理可得,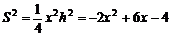
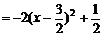 (
(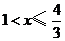 ),
),
易知此时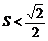 .
.
综合①②得,△ABC的最大面积为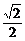 .····································································· 14分
.····································································· 14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com