
12. (石景山·文·题18)
在数列 中,
中,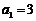 ,
,
 且
且 .
.
⑴求 ,
, 的值;
的值;
⑵证明:数列 是等比数列,并求
是等比数列,并求 的通项公式;
的通项公式;
⑶求数列 的前
的前 项和
项和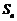 .
.
[解析]
⑴∵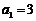 ,
,
 且
且 ,
,
∴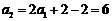 ,
,
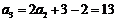 .
.
⑵∵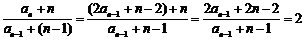 ,
,
∴数列 是首项为
是首项为 ,公比为
,公比为 的等比数列.
的等比数列.
∴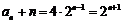 ,即
,即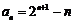 ,
,
∴ 的通项公式为
的通项公式为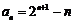
 .
.
⑶∵ 的通项公式为
的通项公式为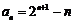
 ,
,
∴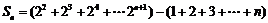

 .
.
11. (石景山·文·题14)(石景山·理·题14)
在数列 中,若
中,若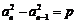 ,(
,(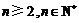 ,
, 为常数),则称
为常数),则称 为“等方差数列”.下列是对“等方差数列”的判断:
为“等方差数列”.下列是对“等方差数列”的判断:
①若 是等方差数列,则
是等方差数列,则 是等差数列;
是等差数列;
② 是等方差数列;
是等方差数列;
③若 是等方差数列,则
是等方差数列,则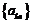 (
(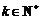 ,
, 为常数)也是等方差数列;
为常数)也是等方差数列;
④若 既是等方差数列,又是等差数列,则该数列为常数列.
既是等方差数列,又是等差数列,则该数列为常数列.
其中正确命题序号为 .(将所有正确的命题序号填在横线上)
[解析] ①②③④;
由定义可知,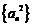 是公差为
是公差为 的等差数列,①正确;
的等差数列,①正确;
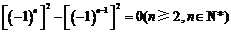 为常数,故
为常数,故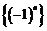 是等方差数列,②正确;
是等方差数列,②正确;
若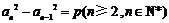 ,则
,则
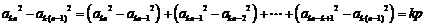 为常数,③对;
为常数,③对;
设 公差为
公差为 ,则
,则 ,结合
,结合 ,两式相减可得
,两式相减可得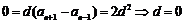 ,故
,故 是常数列,④对.
是常数列,④对.
10. (石景山·文·题12)
等差数列 中,
中,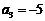 ,
,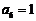 ,此数列的通项公式为 ,设
,此数列的通项公式为 ,设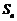 是数列
是数列 的前
的前 项和,则
项和,则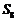 等于 .
等于 .
[解析]
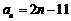 ,
,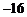 ;
;
设公差为 ,
,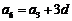 即
即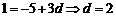 ,
,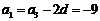 ,
,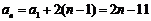 ,
, .
.
9. (东城·文·题11)
设 是等比数列,若
是等比数列,若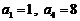 ,则
,则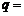 ,数列
,数列 的前
的前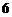 项的和
项的和 .
.
[解析]
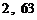 ;
;
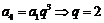 ;
; .
.
8. (丰台·文·题10)
设等比数列 的公比为
的公比为 ,前
,前 项和为
项和为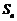 ,则
,则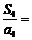 .
.
[解析]
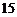 ;
;
 .
.
7. (海淀·理·题8)
已知数列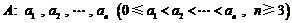 具有性质
具有性质 :对任意
:对任意 ,
,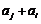 与
与 两数中至少有一个是该数列中的一项.现给出以下四个命题:
两数中至少有一个是该数列中的一项.现给出以下四个命题:
① 数列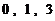 具有性质
具有性质 ;
;
② 数列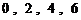 具有性质
具有性质 ;
;
③ 若数列 具有性质
具有性质 ,则
,则 ;
;
④ 若数列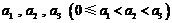 具有性质
具有性质 ,则
,则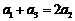 .
.
其中真命题有( )
A.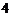 个 B.
个 B. 个 C.
个 C. 个 D.
个 D. 个
个
[解析] B;
①∵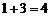 ,
,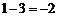 都不在数列中,∴数列
都不在数列中,∴数列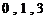 不具有性质
不具有性质 ;
;
②容易验证数列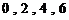 具有性质
具有性质 ;
;
③取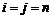 ,则
,则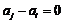 在数列中,而数列中最小的数
在数列中,而数列中最小的数 ,因此
,因此 ;
;
④由对②的分析可知, .由于
.由于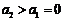 ,
,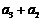
 不在数列中,因此
不在数列中,因此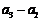 必然在数列中.又
必然在数列中.又 ,故
,故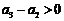
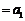 ,于是
,于是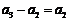 ,等式
,等式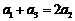 成立.
成立.
6. (丰台·理·题8)
已知整数以按如下规律排成一列: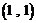 、
、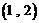 、
、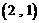 、
、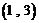 、
、 ,
,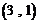 ,
,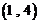 ,
,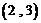 ,
,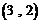 ,
, ,……,则第
,……,则第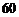 个数对是( )
个数对是( )
A.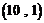 B.
B.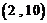
 C.
C.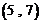 D.
D.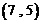
[解析] C;
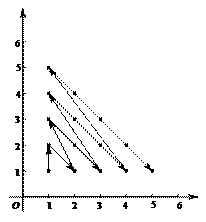
根据题中规律,有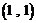 为第
为第 项,
项,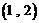 为第2项,
为第2项,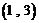 为第4项,…,
为第4项,…,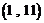 为第
为第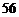 项,因此第
项,因此第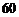 项为
项为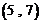 .
.
5. (东城·理·题7)
已知数列 的通项公式
的通项公式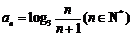 ,设其前
,设其前 项和为
项和为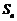 ,则使
,则使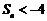 成立的最小自然数
成立的最小自然数 等于( )
等于( )
A.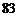 B.
B.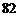 C.
C.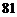 D.
D.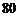
[解析] C;
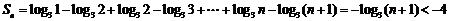 ,解得
,解得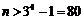 .
.
4. (海淀·理·题6)
已知等差数列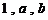 ,等比数列
,等比数列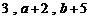 ,则该等差数列的公差为( )
,则该等差数列的公差为( )
A. 或
或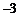 B.
B. 或
或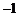 C.
C. D.
D.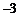
[解析] C;
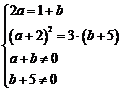 ,解得
,解得 .
.
因此该等差数列的公差为 .
.
3. (宣武·理·题5)(宣武·文·题5)
若 为等差数列,
为等差数列,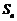 是其前
是其前 项和,且
项和,且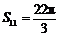 ,则
,则 的值为( )
的值为( )
A.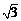 B.
B. C.
C.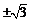 D.
D.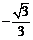
[解析] B;
由 ,可得
,可得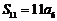 ,∴
,∴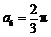 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com