18.(本小题满分15分)

已知椭圆C：＝1(a＞b＞0)的右准线l的方程为x＝，短轴长为2．

(1)求椭圆C的方程；

(2)过定点B(1，0)作直线l与椭圆C相交于P，Q(异于A₁，A₂)两点，设直线PA₁与直线QA₂相交于点M(2x₀，y₀)．

　　　 ①试用x₀，y₀表示点P，Q的坐标；

②求证：点M始终在一条定直线上．

高三数学　 第3页　 共4页

17.(本小题满分15分)如图，A，B，C是三个汽车站，AC，BE是直线型公路．已知AB＝120 km，∠BAC＝75°，∠ABC＝45°．有一辆车(称甲车)以每小时96(km)的速度往返于车站A，C之间，到达车站后停留10分钟；另有一辆车(称乙车)以每小时120(km)的速度从车站B开往另一个城市E，途经车站C，并在车站C也停留10分钟．已知早上8点时甲车从车站A、乙车从车站B同时开出．

(1)计算A，C两站距离，及B，C两站距离；

(2)若甲、乙两车上各有一名旅客需要交换到对方汽车上，问能否在车站C处利用停留时间交换．

(3)求10点时甲、乙两车的距离．

(参考数据：，，，)

16.　　　 (本小题满分14分)

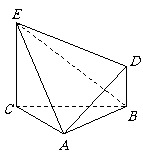
已知△ABC为正三角形，EC⊥平面ABC，DB⊥平面ABC，且EC，

DB在平面ABC的同侧，CE＝CA＝2BD＝2．

(1)求证平面CAE⊥平面DAE；

(2)求：点B到平面ADE的距离．

高三数学　 第2页　 共4页　

15.　 (本小题满分14分) 已知函数

已知＝(，)，＝(cos，sin)，＝3，求：

(1)的值；

(2)向量与的夹角θ的余弦值．

14.　 已知正数x，y满足(1+x)(1+2y)＝2，则4xy+的最小值是　　　　 ．

13.　 在□ABCD中，已知AB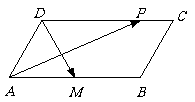＝2，AD＝1，∠DAC＝60°，点M为AB的中点，点P在BC与CD上运动(包括端点)，则的取值范围是　　　　　 ．

12.　 过圆x²+y²＝1上一点P作圆的切线与x轴和y轴分别交于A，B两点，O是坐标原点，

则OA+8·OB的最小值是　　　　　 ．

11.　 已知D是由不等式组所确定的平面区域，则圆x²+y²＝4 围成的区域与区域D的公共部分的面积为　　　　　 ．

10.　 已知f(x)＝x³－3x，过A(1，m)可作曲线y＝f(x)的三条切线，则m的取值范围是　　　　 ．

9.　　 已知cos＝，coscos＝，coscoscos＝，…，根据这些结果，猜想出的一般结论

是