21．(本小题满分13分)

已知数列中，且点在直线上。

　(1)求数列的通项公式;

　(2)若函数求函数的最小值；

　(3)设表示数列的前项和。试问：是否存在关于的整式，使得

对于一切不小于2的自然数恒成立？ 若存在，写出的解析式，并加以证明；若不存在，试说明理由。

解：(1)由点P在直线上，

即，--------------------------------2分

且，数列{}是以1为首项，1为公差的等差数列

　 ，同样满足，所以---------------4分

　 (2)

　　　 ------------6分

　　 所以是单调递增，故的最小值是-----------------8分

(3)，可得，

　　 ，

……

，n≥2

故存在关于n的整式g(x)=n,使得对于一切不小于2的自然数n恒成立----13分

20．(本小题满分13分)

已知椭圆的离心率为，直线与以原点为圆心、椭圆的短半轴长为半径的圆相切。

　(1)求椭圆的方程；

　(2)设椭圆 的左焦点为，右焦点为，直线过点且垂直于椭圆的长轴，动直线垂直于直线,垂足为点,线段的垂直平分线交于点，求点的轨迹的方程；

　(3)设与轴交于点，不同的两点在上，且满足，求的取值范围。

解： (1)由得，又由直线与圆相切，得，，∴椭圆的方程为：。---------------4分

(2)由得动点的轨迹是以为准线，为焦点的抛物线，∴点的轨迹的方程为。--------------------8分

(3)，设，

∴，

由，得，∵

∴化简得，---------------------10分

∴(当且仅当时等号成立)，

∵，

又∵，∴当，即时，

∴的取值范围是---------------------------13分

19．(本小题满分13分)

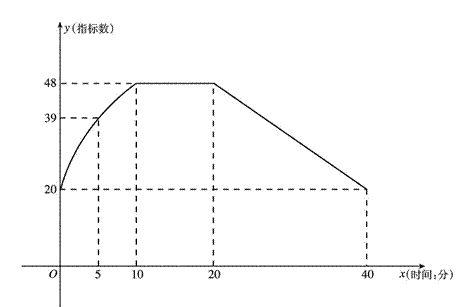
通过实验研究，专家们发现：初中学生听课的注意力指标数是随着老师讲课时间的变化而变化的，讲课开始时，学生的兴趣激增，中间有一段时间，学生的兴趣保持平稳的状态，随后开始分散. 学生注意力指标数y随时间x(分钟)变化的函数图象如图所示(y越大表示学生注意力越集中). 当时，图象是抛物线的一部分，当和时，图象是线段.

(1)当时，求注意力指标数y与时间x的函数关系式；

(2)一道数学竞赛题需要讲解24分钟. 问老师能否经过适当安排，使学生在听这道题时，注意力的指标数都不低于36.

解：(1)当时，设抛物线的函数关系式为，由于它的图象经过点(0，20)，(5，39)，(10，48)，所以

解得，，，.

所以，.　 ………………(6分)

(2)当时，.

所以，当时，令y=36，得，

解得x=4，(舍去)；

当时，令 y=36，得，解得

. 　　　　…………………(13分)

因为，所以，老师可以经过适当的安排，在学生注意力指标数不低于36时，讲授完这道竞赛题。

18．(本小题满分12分)

如图是某三棱柱被削去一个底面后的直观图与侧视图、俯视图.已知 ，侧视图是边长为2的等边三角形；俯视图是直角梯形，有关数据如图所示.

(Ⅰ)求该几何体的体积；

(Ⅱ)求二面角的余弦值.

解:(Ⅰ)

.

，∴，∴.

∴.

…………5分

(Ⅱ)OA，OR.。

则，∴，。

又∵，以为原点，所在直线分别为轴，建立空间直角坐标系，则

，显然二面角的平面角为钝角，

所以二面角的余弦值为.…………………………………12分

17．(本小题满分12分)

某篮球职业联赛的总决赛在甲队与乙队间角逐，采用五局三胜制，即若一队先胜三场，则此队获胜，比赛结束，因两队实力相当，每场比赛获胜的可能性相等，据以往资料统计，第一场比赛组织者可获门票收入30万元，以后每场比赛门票收入都比上一场增加10万元，问：

　　 　⑴组织者在此次总决赛中获得门票收入不少于180万元的概率是多少？

　　 　⑵用表示组织者在此次总决赛中的门票收入，求的数学期望？

解：⑴每场比赛的门票收入构成等差数列{a_n}，其中a₁=30，d=10，

　　　 S_n=5n²+25n

　　　 令S_n≥180,即5n²+25n≥180，解得n≥4或n≤-9(舍)

　　　 ∴n=4或5

　　　 …………………………………6分

　　　 ⑵

	120	180	250
P

∴E=…………………………………………12分

16．(本小题满分12分)

已知函数(其中为正常数，)的最小正周期为．

(1)求的值；

(2)在△中，若，且，求．

解：(1)∵

．　　 ……………4分

而的最小正周期为，为正常数，∴，解之，得． ………………………6分

(2)由(1)得．

若是三角形的内角，则，∴．

令，得，∴或，

解之，得或．

由已知，是△的内角，且，

∴，，∴

．　　　　　　　　　　 …………………………10分

又由正弦定理，得．　　　　　　 …………………………12分

15．已知△ABC内接于半径为1的圆O,且满足,

则∠AOB=　　 90°　　 ,△ABC的面积S=　 　　　　　　　　.

14．已知，

则=　　 　-8　 　　．

13.在上任取两个数，那么函数无零点的概率为________.

12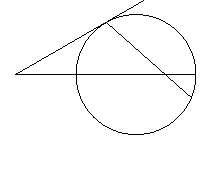．如图4，已知是⊙的切线，是切点，直线交⊙于、两点，是的中点，连结并延长交⊙于点．若，，则=　 ．