
9.(1)设从今年起的第 年(今年为第1年)该企业人均发放年终奖为
年(今年为第1年)该企业人均发放年终奖为 万元.则
万元.则
 ; ………………………………………4分
; ………………………………………4分
解法一:由题意,有 ,…………………………………………1分
,…………………………………………1分
解得, .………………………………………………………………1分
.………………………………………………………………1分
所以,该企业在10年内不能实现人均至少3万元年终奖的目标.……………1分
解法二:由于 ,所以
,所以 …2分
…2分
所以,该企业在10年内不能实现人均至少3万元年终奖的目标.……………1分
(2)解法一:设 ,则
,则


 ,………………………………4分
,………………………………4分
所以, ,得
,得 . ………………………………………2分
. ………………………………………2分
所以,为使人均发放的年终奖年年有增长,该企业员工每年的净增量不能超过23人.
……………………………………………………………………………………1分
解法二:
……………………………………………………………………………………4分
由题意,得 ,解得
,解得 . ……………………………2分
. ……………………………2分
所以,为使人均发放的年终奖年年有增长,该企业员工每年的净增量不能超过23人.
……………………………………………………………………………………1分
10(本题满分16分)
如图所示,某人在斜坡P处仰视正对面山顶上一座铁塔,塔高AB=80米,塔所在山高OA=220米,OC=200米,观测者所在斜坡CD近似看成直线,斜坡与水平面夹角为 ,
,
(1)以射线OC为 轴的正向,OB为
轴的正向,OB为 轴正向,建立直角坐标系,求出斜坡CD所在直线方程;
轴正向,建立直角坐标系,求出斜坡CD所在直线方程;
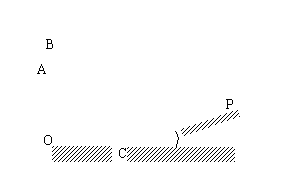 (2)当观察者P视角∠APB最大时,求点P的坐标(人的身高忽略不计).
(2)当观察者P视角∠APB最大时,求点P的坐标(人的身高忽略不计).
 |
|||
|
|||
9.(本题满分14分)本题有2小题,第1小题6分,第2小题8分.
某企业去年年底给全部的800名员工共发放2000万元年终奖,该企业计划从今年起,10年内每年发放的年终奖都比上一年增加60万元,企业员工每年净增 人.
人.
(1)若 ,在计划时间内,该企业的人均年终奖是否会超过3万元?
,在计划时间内,该企业的人均年终奖是否会超过3万元?
(2)为使人均年终奖年年有增长,该企业每年员工的净增量不能超过多少人?
8. 设 表示不超过
表示不超过 的最大整数,如
的最大整数,如 .若函数
.若函数 ,则
,则 的值域为______
的值域为______  _______
_______
7.已知 ,则
,则

6.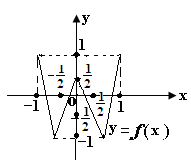 已知函数
已知函数 的定义域和值域都是
的定义域和值域都是 (其图像如下图所示),
(其图像如下图所示),
函数 .定义:当
.定义:当 且
且
时,称 是方程
是方程 的一个实数根.则方程
的一个实数根.则方程 的所有不同实数根的个数是 8
的所有不同实数根的个数是 8
5.已知曲线 :
: ,下列叙述中正确的有 (1).(2).(4) .
,下列叙述中正确的有 (1).(2).(4) .
(1).垂直于 轴的直线与曲线
轴的直线与曲线 只有一个交点
只有一个交点
(2).直线 (
( )与曲线
)与曲线 最多有三个交点
最多有三个交点
(3).曲线 关于直线
关于直线 对称
对称
(4).若 ,
, 为曲线
为曲线 上任意两点,则有
上任意两点,则有
4.已知数列 满足:
满足: (
( 为正整数),
为正整数), 若
若 ,则
,则 所有可能的取值为 56和9 .
所有可能的取值为 56和9 .
3.设函数 和
和 都在区间
都在区间 上有定义,若对
上有定义,若对 的任意子区间
的任意子区间 ,总有
,总有 上的实数
上的实数 和
和 ,使得不等式
,使得不等式 成立,则称
成立,则称 是
是 在区间
在区间 上的甲函数,
上的甲函数, 是
是 在区间
在区间 上的乙函数.已知
上的乙函数.已知 ,那么
,那么 的乙函数
的乙函数
 .
.
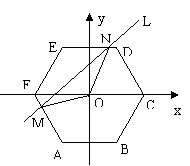
2.如图,在直角坐标平面内有一个边长为 ,中心在原点
,中心在原点 的
的
正六边形 ,
, . 直线
. 直线
与正六边形交于M、N两点,记 的面积为
的面积为 ,则函数
,则函数
 的奇偶性为 偶函数
的奇偶性为 偶函数
1. 设双曲线
设双曲线 的半焦距为
的半焦距为 .已知原点到直线
.已知原点到直线 :
: 的距离等于
的距离等于 ,则
,则 的最小值为_____4.____
的最小值为_____4.____
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com