12、已知A、B为椭圆的左右两个顶点，F为椭圆的右焦点，P为椭圆上异于A、B点的任意一点，直线AP、BP分别交椭圆的右准线于M、N两点，则△MFN面积的最小值是(　 )A．8　　　　 B．9　　　　　　　 C．11　　　　　　 D．12

11、来自中国、英国、瑞典的乒乓球裁判各两名，执行北京奥运会的一号、二号和三号场地的乒乓球裁判工作，每个场地由两名来自不同国家的裁判组成，则不同的安排方案总数有(　 )

A．12种　　　　 B．48种　　　　 C．90种　　　　 D．96种

9、已知函数，其图像与直线y=2某两个交点的横坐标分别为，则该函数在区间(　 )上是增函数。

A．　　　　　　 B．　　　　 C．　　　　　　 D．

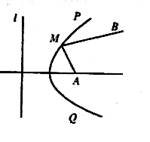1 0、如图，l表示南北方向的公路，A地在公路的正东2km处，B地在A地北偏东60°方向km处，河流沿岸PQ(曲线)上任一点到公路l和到A地距离相等，现要在河岸PQ上选一处M建一座码头，向A、B两地转运货物，经测算从M到A、B修建公路的费用均为a万元/km，那么修建这两条公路的总费用最低是

　 A．　 B．5a　　 C．　 D．6a

8、已知等差数列，则等于(　 )　 A． 　　　 B．　　　　　　 C．1　　　　　　　 D．2

7、

6、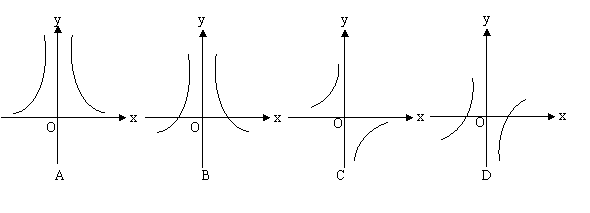函数的大致图象是(　 )

5、在空间中，有如下命题：①互相平行的两条直线在同一平面内的射影必然是互相平行的两条直线；②若平面内任意一条直线都平行平面，则平面//平面；③若平面与平面的交线为m，平面内的直线n⊥直线m，则直线n⊥平面；④若平面内有两条相交直线都和平面内一条直线垂直，则⊥。其中正确命题的个数为

A．1个　　　　 B．2个　　　　　 C．3个　　　　 D．4个

2、条件p: ，条件q：函数在区间[-1,2]上存在的

A．充分非必要条件 　　　　　　　　 B．必要非充分条件 　

C．充分必要条件 　　　　　　　　　　 D．既非充分也非必要条件

22、已知数列，，其中，数列的前项和，数列满足，．

(Ⅰ)求数列，的通项公式；(Ⅱ)是否存在自然数，使得对于任意，，有恒成立？若存在，求出的最小值；

(Ⅲ)若数列满足当是偶数时，求数列的前项和．

21、已知函数在x=-1处取得极值，在x=-2处的切线与直线x-8y=0垂直。

(1)求常数a,b,c的值；

(2)对于函数，若存在常数k,m，对于任意都成立，则称直线是函数的分界线，求函数与函数的“分界线”方程。