22、已知数列

(1)求数列的通项公式；

(2)比较

(3)证明:

		座 位 号

21、已知点P是圆O: 上的动点，以点P为切点的切线与x轴相交于点Q，直线OP与直线x=1相交于点N，若动点M满足：，记动点M的轨迹为曲线C。

(1)求曲线C的方程；

(2)若过点F(2,0)的动直线与曲线 C相交于不在坐标轴上的两点A,B，设，问在x轴上是否存在定点E，使得？若存在，求出点E的坐标，若不存在；说明理由。

20、已知函数为自然对数的底，且为常数)

(1)讨论函数的单调性；

(2)对于函数，若存在常数k,m，对于任意都成立，则称直线是函数的分界线，设a=1，问函数与函数是否存在“分界线”？若存在，求出常数k,m，若不存在，说明理由。

19、上海世博会即将开幕，某调查公司调查了南昌市某单位一办公室4位员工参观世博会意愿及消费习惯，得到结论如右表，

(1)求这4位员工中恰好有2位员工参观世博会的概率。

参观世博会的概率 参观世博会的消费金额(单位：元) 员工1 3000 员工2 3000 员工3 4000 员工4 4000

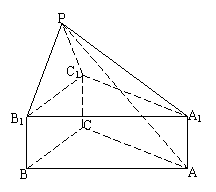18、如图，正三棱柱 ABC-A₁B₁C₁中，AB=2, AA₁=1，点P在平面BCC₁B₁内，PB₁=PC₁=。

(1)求证：PA₁⊥BC; (2)求二面角C₁-PA₁-A。

17、

16、已知正四棱柱ABCD-A₁B₁C₁D₁的底面边长AB=6，侧棱长AA₁=，它的外接球的球心为O，点E是AB的中点，点P是球O的球面上任意一点，有以下判断：

①PE长的最大值为9；②三棱锥P-EBC体积的最大值是；③存在过点E的平面，截球O的截面面积是；④三棱锥P-AEC₁体积的最大值是20，正确的是　　　　 。

15、设函数的小数点后第n位数，则的值为　　　　 。

14、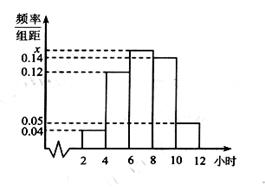某校为了解高三同学寒假期间学习情况，抽查了100名学生，统计他们每天平均学习时间，绘成频率分布直方图(如图)。则这100名同学中学习时间6~8小时的人数为　　　　　 。

13、的展开式中常数项为　　　　 。(用数字作答)