4．对英王查理一世的审判与处死是英国革命中的重大事件。布拉德肖法官曾在法庭上向查理一世宣示：“在国王和他的人民之间存在一个契约协定……这就好像一条纽带，纽带的一头是君主对国民应尽的保护义务，另一头是国民对君主应尽的义务。先生，一旦这条纽带被切断，那么只能说，别了，君主统治！”上述材料表明，布拉德肖比法国启蒙思想家更早提出了

A．君主立宪的观点　　　　　　　　　　　 B．革命权利的学说

C．社会契约的理念　　　　　　　　　　　 D．天赋人权的思想

3．　 英国女王伊丽莎白(1533--1603)曾经说：海洋和空气为世界人共同享有，海洋不归属于任何民族或任何个人。这段话主要是针对

A．法国　　　　　 B．荷兰　　　　　 C．西班牙　　　　 D．意大利

2．下列现象出现于文艺复兴时期的意大利，能够体现人文主义思想的有：

①彼特拉克在《歌集》中抒发对妻子真挚的爱情；

②许多富商建造的宅第带有美丽的花园和宽敞的阳台；

③很多学校和教师都把培养良好的行为习惯作为学生的必修课；

④出现了用方言翻译的《圣经》

A．③④　 　　　　B．①②③ 　　　　　　 C．①③④ 　　　　　　　 D．①②③④

1．1522年9月6日，某国国王举行褒奖仪式，特地制作了一个地球仪，赠送给生还的18位勇士，说：“你们第一个拥抱了地球。”该国王是　　　　　　

A．西班牙国王　　　 　 B．英国国王

　　　 C．葡萄牙国王　　　　 　　　　　　　　　　　　　 D．荷兰国王

∵点A(1，)，即OC=1，AC=，

∴∠AOC= 60°，OA=2.　　 …………………………………………1分　　

∴ 点B(-2，0).　　　 　　…………………………………………2分

⑵ ∵抛物线经过点O(0，0)，

　∴可设所求解析式为y= ax²+bx.

把点A、B的坐标代入，

得 　　　　　　……………………………………………3分

解得 a=，b=.

∴所求解析式为y =x²+x .　 　…………………………………4分

⑶ 存在，

∵点O和B关于抛物线y =x²+x的对称轴直线x= -1对称，

∴直线AB与直线x= -1的交点即为所求点P.　　　 ……………… 5分

把点A(1，)、B(-2，0)分别代入y=kx+b，

可求得直线AB的解析式为：y =x+.　　 ……………………6分

令x= -1，得y=.

∴ 点P(-1，).　　　　 …………………………………………7分

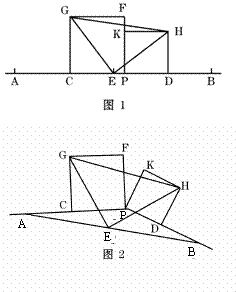
26.⑴证明：∵C、D、E分别是AP、PB、AB的中点，

∴CE=AE-AC=AB-AP=(AB-AP)=BP=DP.　 ………………1分

∴ CE+EP=DP+EP，即CP=DE.

∵四边形CPFG和PDHK都是正方形，

∴在△CEG和△DHE中，

CE= DP=DH，CG=CP=DE, ∠GCE=∠EDH=90°.

∴△CEG≌△DHE .　　　　　　　　 ………………………………2分

∴EG= HE，∠EGC =∠HED.

而∠EGC+∠CEG=90°，

∴∠HED+∠CEG=90°.

∴∠GEH=90°.

又∵EG= HE，

∴△EHG是等腰直角三角形.　　　　

………………………………3分

⑵ 　△EHG还是等腰直角三角形.　　 　　　　　

………………………………4分

理由如下：

联结CE、ED，得□CEDP，

可知∠PCE=∠PDE.

进而得∠GCE=∠EDH，

再由CE=BP=DP=DH，

CG=CP=AP=DE，

仍可证△CEG≌△DHE .　　　　　　　 …………………………………5分

∴EG= HE，∠EGC =∠HED.

如图，设EG和CP相交于M，

则∠GEH=∠GED-∠HED，

　　　　 =∠GMP-∠EGC

　　　　 =∠GCM

　　　　 =90°

∴ △EHG是等腰直角三角形..　　 　　　……………………………………6分

⑵ 40.5~60.5　　　　　 　　　………………………………………………4分 　 ⑶ 样本容量为4+5+6+3+2=20(人)， 　　 其中在寒假做家务时间超过40.5小时的共有6+3+2=11(人)， 　　　 180×=99(人)，

　答：估计该年级有99人在寒假做家务时间超过40.5小时。 …………6分

24. ⑴ 相切　 　　　　　　　　　…………………………………………1分

证明：联结OC，并且知道证CP⊥OC .　 　　…………………………2分

　　 能完成证明　　 　　　　　……………………………………4分

⑵ 能求得PC =　　　　　 　　………………………………………6分

22. ⑴ 当0≤x≤6时，y=3x；　　　　　 ………………………………1分

当x＞6时，y=18+5(x-6)=5x-12.　

　　 ∴y =　　　 ………………………………………2分

　　 画图正确(需表达出至少两个点的坐标，例如(6，18)、(10，38)) …………………………………3分

　 ⑵ 设小明家今年3月份用水x吨.

∵35 ＞(3×6=18)，　 ∴x＞6.

依题意，得5x -12=35, 　　……………………………………………4分

解得　　 x=9.4 　

答：小明家今年3月份用水9.4吨.　 …………………………………5分

21. 如图1，分别过点A、D作AE⊥BC于点E ，

DF⊥BC于点F．　 ………………………………1分

∴ AE // DF．又 AD // BC，

∴ 四边形AEFD是矩形．

∴ EF=AD=1． 　　……………………………………2分

∵ AB⊥AC，∠B=45°，BC= 4，

∴ AB=AC．

∴ AE=EC== 2．　 ……………………………3分

∴ DF=AE= 2，

CF=EC-EF= 1． 　　　……………………………4分

在Rt△DFC中，∠DFC=90°，

∴DC=.　　 …………………………5分

20. 原式=　　　 ………………………………………3分

= -　　　　　 　　　　　　……………………………………4分 ∴当x=2010时，　　　

原式= - = -　　　 ………………………………………5分

19. 证明：∵ AB∥DE，　 　　 ∴∠ABC =∠DEF.　　　　 ……………………………………………1分

　　　　　 ∵ BE=CF，

　　　　　 ∴BE+CE= CF+CE，即BC=EF. 　　……………………………………2分

在△ABC和△DEF中，　

又∵∠ACB =∠DFE，

∴△ABC≌△DEF. 　　　　　……………………………………………3分

∴ AC=DF .　　　　　　　　　　 ………………………………………4分