
20.(本题满分13分)
设函数 .
.
(1)讨论函数 的单调性;
的单调性;
(2)判断方程 的实数解的个数,并加以证明。
的实数解的个数,并加以证明。
19.(本题满分12分)
设椭圆 的两个焦点是
的两个焦点是 ,且椭圆上存在点M,使
,且椭圆上存在点M,使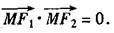
(1)求实数m的取值范围;
(2)若直线 与椭圆存在一个公共点E,使得|EF
与椭圆存在一个公共点E,使得|EF |+|EF
|+|EF |取得最小值,求此最小值及此时椭圆的方程;
|取得最小值,求此最小值及此时椭圆的方程;
(3)在条件(2)下的椭圆方程,是否存在斜率为 的直线
的直线 ,与椭圆交于不同的两A,B,满足
,与椭圆交于不同的两A,B,满足 ,且使得过点
,且使得过点 两点的直线NQ满足
两点的直线NQ满足 =0?若存在,求出k的取值范围;若不存在,说明理由
=0?若存在,求出k的取值范围;若不存在,说明理由
18.(本题满分12分)
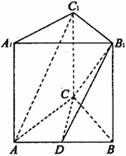
如图,在直三棱柱 中,
中, ,AC=BC CC
,AC=BC CC ,D为
,D为
AB的中点.
(1)求证:
(2)求二面角B-B C-D的余弦值的大小。
C-D的余弦值的大小。
17.(本题满分12分)
四个大小相同的小球分别标有数字1、1、2、2,把它们放在一个盒子中,从中任意摸出两个小球,它们的标号分别为 ,记=
,记=
(1)求随机变量的分布列及数学期望;
 (2)设“函数
(2)设“函数 在区间(2,3)上有且只有一个零点”为事件A,求事件A发生的概率。
在区间(2,3)上有且只有一个零点”为事件A,求事件A发生的概率。
16.(本题满分12)
已知函数 ,且给定条件
,且给定条件 ,
,
(1)求 的最大值及最小值;
的最大值及最小值;
(2)若又给条件 且,p是q的充分条件,求实数m的取值范围。
且,p是q的充分条件,求实数m的取值范围。
15.如图是一几何体的平面展开图,其中ABCD为正方形,E、F分
别为PA、PD的中点,在此几何体中,给出下面四个结论:
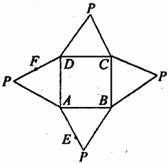 ①直线BE与直线CF异面;
①直线BE与直线CF异面;
②直线BE与直线AF异面;
③直线EF//平面PBC;
④平面BCE 平面PAD
平面PAD
其中正确的有______________个
14.函数 图象上有且仅有两个点到
图象上有且仅有两个点到 轴距离等于1,则a的取值范围是_______.
轴距离等于1,则a的取值范围是_______.
13.已知 满足条件
满足条件 ,则
,则 的取值范围是_______________。
的取值范围是_______________。
12.若数列{ }满足
}满足 ,则数列{
,则数列{ }为“调和数列”,已知数列{
}为“调和数列”,已知数列{ }为“调和数列”,且
}为“调和数列”,且 ,则
,则 的最大值是_______。
的最大值是_______。
11.坐标原点为O,抛物线 与过其焦点的直线交于A、B两点,则
与过其焦点的直线交于A、B两点,则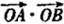 =_________
=_________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com