6．西方人奉古希腊、古罗马文明为西方文明之源。英国历史学家约翰•索利曾说：“如今有个趋势，人民怀念她的民主制度，并将其视为所有现代民主制度的源头。”这里的“她”是指

A．斯巴达　　　　　　 　　　　　　　　 B．雅典　 　

C．罗马共和国　　 　　　　　　　　 D．罗马帝国

5．古罗马文明对人类文明最大的贡献是

A．建立共和政体　　　　　　　　 B．形成了古代世界最完备的法律体系

C．设立保民官　　 　　　　　　　　D．建立地跨欧、亚、菲三洲的大帝国

4．清朝专制皇权高度发展的重要标志是

A．察举制的创立　　　　　　　　 B．内阁的设立

C．三省六部制的创立　　　　　　 D．军机处的设立

3．在中国古代，下列哪一选官制度的出现，改变了魏晋南北朝时期“上品无寒门，下品无士族”的局面　

A．察举制　　　 B．征辟制　　　 C．九品中正制　　　 D．科举制

2．自以为功过三皇，德兼五帝，创立皇帝称号的是

A．大禹　　　　 B．成汤　　　　 C．周武王　　 　　　D．秦王嬴政

1．右图是明清古建筑中的一幅牌匾，其反应的中国古代

政治制度是

A．分封制　　　　　　　　　　　 B．宗法制　

C．三省六部制　　　　　　　　　 D．内阁制

　(17)(本小题满分12分)

已知函数在一个周期内的图象如图所示。

(Ⅰ)求的值；

(Ⅱ)在中，设内角所对边的长分别是，若的面积，求的大小。

　(18)(本小题满分12分)

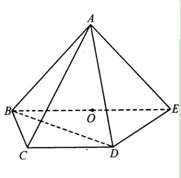
如图，在四棱锥中，底面为梯形，点在底面内的射影恰为线段的中点，直线与底面所成的角为。

(Ⅰ)求证：；

(Ⅱ)求二面角的大小。

　 　(19)(本小题满分12分)

某研究小组在电脑上进行人工降雨模拟试验，准备用A、B、C三种人工降雨方式分别

对甲、乙、丙三地实施人工降雨，其试验数据统计如下

假定对甲、乙、丙三地实施的人工降雨彼此互不影响，请你根据人工降雨模拟试验的统

计数据

　　 (I)求甲、乙、丙三地都恰为中雨的概率；

　　 (Ⅱ)考虑到旱情和水土流失，如果甲地恰需中雨即达到理想状态，乙地必须是大雨才达到理想状态，丙地只能是小雨或中雨即达到理想状态，记“甲、乙、丙三地中达到理想状态的个数”为随机变量ξ，求随机变量ξ的分布列和数学期望Eξ．

　(20)(本小题满分12分)

设动圆M满足条件p：经过点F(，0)，且与直线l：相切；记动圆圆心M的轨

迹为C．

　 　(Ⅰ)求轨迹C的方程；

(Ⅱ)已知点为轨迹C上纵坐标为m的点，以为圆心满足条件P的圆与X轴相交于点F、A(A在F的右侧)，又直线与轨迹C相交于两个不同点，当 (O为坐标原点)时，求直线，的斜率．

　(21)(本小题满分12分)

已知数列的前项和为，且当时，。

(Ⅰ)求的值；

(Ⅱ)若，求数列的通项公式；

(Ⅲ)设数列的前项和为，证明：。

　(22)(本小题满分14分)

已知函数，其导函数为，令.

(Ⅰ)设，求函数的极值;

(Ⅱ)设

①求证：；

②是否存在正整数，使得当时，都有成立?若存在，求出一个满足条件的的值；若不存在，请说明理由。

16.如果函数f(x)同时满足下列条件：①在闭区间[a,b]内连续，②在开区间(a,b)内可导且其导函数为f'(x)，那么在区间(a,b)内至少存在一点ξ(a＜ξ＜b)，使得f(b)－f(a)＝f'(ξ)(b－a)成立，我们把这一规律称为函数f(x)在区间(a,b)内具有“Lg”性质，并把其中的ξ称为中值。有下列命题： ①若函数f(x)在(a,b)具有“Lg”性质，ξ为中值，点A(a,f(a)),B(b,f(b))，则直线AB的斜率为f'(ξ)； ②函数y＝在(0,2)内具有“Lg”性质，且中值ξ＝,f'(ξ)＝－; ③函数f(x)＝x³在(－1,2)内具有“Lg”性质，但中值ξ不唯一； ④若定义在[a,b]内的连续函数f(x)对任意的x₁、x₂∈[a,b],x₁＜x₂，有[f(x₁)+f(x₂)]＜f()恒成立，则函数f(x)在(a,b)内具有“Lg”性质，且必有中值ξ＝. 其中你认为正确的所有命题序号是___________________. 解析：对于①，根据导函数的几何意义立即可得正确； 对于②，函数y在(0,2)上连续且可导，代值计算可得两端点连线的斜率为－ 又y'＝，当x＝时，y'＝－，故②正确。

对于③，两端点连线斜率为3 而f'(x)＝3x²，令3x²＝3　 Þ　 x＝±1，在(－1,2)内只有一个中值ξ＝1，故③错误； 对于④，[f(x₁)+f(x₂)]＜f()只能保证f(x)是上凸函数，不能保证中值一定在中点处。④错误 答案：①②

15.如图，ABCD为菱形，CEFB为正方形，平面ABCD⊥平面CEFB，CE＝1， ∠AED＝30°，则异面直线BC与AE所成角的大小为__________________. 解析：由题意，正方形和菱形变成均为1， 又平面ABCD⊥平面CEFB，所以CE⊥平面ABCD 于是CE⊥CD，从而DE＝ 在△ADE中，AD＝1, DE＝,∠AED＝30° 由正弦定理得： 所以sin∠DAE＝＝ 故∠DAE＝45° 又BC∥AD，故异面直线BC与AE所成角等于∠DAE

答案：45°

14.已知sin(α+β)cosα－cos(α+β)sinα＝，则cos2β的值为________________. 解析：因为sin(α+β)cosα－cos(α+β)sin

　　　　 ＝sin[(α+β)－α] 　　　　 ＝sinβ＝ 　　　 于是cos2β＝1－2sin²2β＝1－ 答案：