13.如果直线l₁：3x－4y－3＝0与直线l₂关于直线x＝1对称，则直线l₂的方程为______________. 解法一：l₁与l₂关于直线x＝1对称， 由于x＝1斜率不存在，故l₁与l₂斜率互为相反数，且它们与x＝1交于同一点(1,1) 可得直线l₂的方程为3x+4y－3＝0。 解法二：设P(x,y)是l₂上任意一点，则点P关于x＝1的对称点Q(2－x,y)在l₁上 所以3(2－x)－4y－3＝0 整理得：3x+4y－3＝0，此即l₂的方程。 答案：3x+4y－3＝0

12.设f(x)是定义在R上的偶函数，对x∈R，都有f(x－2)＝f(x+2)，且当x∈[－2,0]时，f(x)＝()^x－1，若在区间(－2，6]内关于x的方程f(x)－log_a(x+2)＝0(a＞1)恰有3个不同的实数根，则a的取值范围是(　　 )

(A)(1,2)　 (B)(2，+∞)　 (C)(1,)　　 (D)(,2) 解析：由f(x－2)＝f(x+2)，知f(x)是周期为4的周期函数 于是可得f(x)在(－2,6]上的草图如图中实线所示 而函数g(x)＝log_a(x+2)(a＞1)的图象如图中虚线所示 结合图象可知，要使得方程f(x)－log_a(x+2)＝0(a＞1) 在区间(－2，6]内恰有3个不同的实数根， 必需且只需 所以 解得：＜a＜2 答案：Dw

11.如图为12个单位正方形组成的长方形图形，若沿格线从左下角顶点A走到右上角顶点B，每步只走一个单位长度，则所有最短路线的走法中，经过点C的走法种数是(　　 ) (A)42　　　　　　　　　　　　　　　　　 (B)35 (C)20　　　　　　　　　　　　　　　　　 (D)15 解析：从A到C的最短路线只有2种 从C到B横向有3段路，纵向有2段路，共5段路，其最短路线走法有C₅²＝10种， 故共有2×10＝20种 答案：C

10.设A、B为双曲线 ＝λ(λ≠0)同一条渐近线上的两个不同的点，已知向量m＝(1,0)，|AB|＝6，＝3，则双曲线的离心率e等于(　　 )

(A)2 (B) (C)2或　　 (D)2或 解析：注意到向量m＝(1,0)是x轴上的单位向量，＝3表示向量在x轴上的射影长为3 而|AB|＝6，因此A、B点所在的渐近线与x轴的夹角为60°. (1)当λ＞0时，有＝tan60°　 Þ　 b＝ 　 所以c²＝a²+b²＝4a²　 Þ　 e＝＝2 (2)当λ＜0时，有＝tan60°　 Þ　 a＝b 　 所以c²＝a²+b²＝4b²　 Þ　 e＝

答案：D

9、　　 设数列{a_n}是项数为20的等差数列，公差d∈N^*，且关于x的方程x²+2dx－4＝0的两个实根x₁、x₂满足x₁＜1＜x₂，则数列{a_n}的偶数项之和减去奇数项之和的结果为(　　 ) (A)15　　　　　　　　　　　　　 (B)10　　　　　　　　　　　　　　　　　 (C)5　　　　　　　　　　　　　　　　　　 (D)－20 解析：记f(x)＝x²+2dx－4 则函数f(x)的图象与x轴的两个交点分别在1的两侧 注意到f(x)开口向上， 故f(1)＜0　 Þ　 d＜ 又d∈N^*，故d＝1 又a_2n－a_2n－1＝d 所以(a₂₀+a₁₈+a₁₆+……+a₂)－(a₁₉+a₁₇+a₁₅+……+a₁) 　 ＝(a₂₀－a₁₉)+(a₁₈－a₁₇)－……－(a₂－a₁) 　 ＝10d＝10 答案：B

8、　　 某物流公司有6辆甲型卡车和4辆乙型卡车，此公司承接了每天至少运送280t货物的业务，已知每辆甲型卡车每天的运输量为30t，运输成本费用为0.9千元；每辆乙型卡车每天的运输量为40t，运输成本为1千元，则当每天运输成本费用最低时，所需甲型卡车的数量是(　　 ) (A)6　　　　　　　　　　　　　　 (B)5　　　　　　　　　　　　　　　　　　 (C)4　　　　　　　　　　　　　　　　　　 (D)3 解析：设需要甲型卡车x辆，乙型卡车y辆 由题意且x、y∈Z 运输成本目标函数z＝0.9x+y 画出可行域(如图)可知，当目标函数经过A(4,4)时，z最小7.6千元 及需要甲型卡车和乙型卡车各4辆。 答案：C

6、　　 计算cot15°－tan15°的结果是(　　 ) (A)　　　　　　　　　　　　　 (B) 　　　　　　　　　　　　　　　 (C)3　　　　　　　　　　　　　　　 (D)2 解法一：cot15°－tan15° 　　　 ＝cot(45°－30°)－tan(45°－30°) 　　　 ＝ 　　　 ＝ 　　　 ＝(2+)－(2－) 　　　 ＝2 解法二：cot15°－tan15° 　　　 ＝ 　　　 ＝ 　　　 ＝ 答案：D

7、　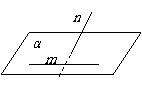　 设m、n为不重合的两条直线，α、β为不重合的两个平面，下列命题为真命题的是(　　 ) (A)如果m、n是异面直线，mÌα，nËα，那么n∥α； (B)如果m、n是异面直线，mÌα，nËα，那么n与α相交； (C)如果m、n共面，mÌα，n∥α，那么m∥n； (D)如果mÌβ，m∥α，nÌα，n∥β，那么m∥n. 解析：如图，可知(A)不正确 对于(B)，当n与α平行时，也可以满足m与n异面的条件，故(B)不正确 对于(C)，因为m、n共面，可设这个平面为γ，又因为mÌα，故m是平面α与γ的交线 根据线面平行的性质定理，当n∥α时，必定有m∥n。(C)正确 对于(D)，当α与β相交时命题正确，但当α∥β时，m、n可能是异面直线。故(D)错误 答案：C

5、　　 设函数f(x)＝x²+2(－2≤x＜0)，其反函数为f^－1(x)，则f^－1(3)＝(　　 ) (A)－1　　　　　　　　　　　　 (B)1　　　　　　　　　　　　　　　　　　 (C)0或1　　　　　　　　　　　　　　 (D)1或－1 解析：令f(t)＝3，则t＝f^－1(3) (－2≤t＜0) 　　　 有t²+2＝3　 Þ　 t＝±1 　　　 但－2≤t＜0，故t＝－1 答案：A

4、　　 已知向量a＝(－3,2),b＝(2,1),则|a+2 b|的值为(　　 ) (A)3　　　　　　　　　　　 (B)7　　　　　　 (C)　　　　　　　　　　　　　　　　　　　　　 　　　　　 (D)解析：因为a+2 b＝(1,4) 　　　 故|a+2 b|＝ 答案：C

3、　　 若复数z＝(m²－1)+(m+1)i为纯虚数，则实数m的值等于(　　 ) (A)1　　　　　　　　　　　　　　 (B)0　　　　　　　　　　　　　　　　　　 (C)－1　　　　　　　　　　　　　　　　 (D)±1 解析：由题意　 Þ　 m＝1答案：A