
3.公差不为零的等差数列的第二、三、六项依次成等比数列,则公比是 ( )
A.2 B.3 C.4 D.5
2.复数 ,则复数
,则复数 在复平面内对应的点位于 ( )
在复平面内对应的点位于 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
1.已知人订合 ,则M∩N= ( )
,则M∩N= ( )
A. B.
B. C.
C. D.
D.
6. 已知函数 的反函数为
的反函数为 ,数列
,数列 和
和 满足:
满足: ,
, ,函数
,函数 的图象在点
的图象在点 处的切线在
处的切线在 轴上的截距为
轴上的截距为 .
.
(Ⅰ)求数列{ }的通项公式;
}的通项公式;
(Ⅱ)若数列 的项仅
的项仅 最小,求
最小,求 的取值范围;
的取值范围;
(Ⅲ)令函数 ,
, ,数列
,数列 满足:
满足: ,
, ,且
,且 ,其中
,其中 .证明:
.证明: .
.
5.已知 ,点
,点 满足
满足 ,记点
,记点 的轨迹为
的轨迹为 .
.
(Ⅰ)求轨迹 的方程;
的方程;
(Ⅱ)若直线 过点
过点 且与轨迹
且与轨迹 交于
交于 、
、 两点. (i)设点
两点. (i)设点
 ,问:是否存在实数
,问:是否存在实数 ,使
,使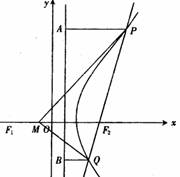 得直线
得直线 绕点
绕点 无论怎样转动, 都有
无论怎样转动, 都有 成立?若存在,求出实数
成立?若存在,求出实数 的值;若不存在,请说明理由.(ii)过
的值;若不存在,请说明理由.(ii)过 、
、 作直线
作直线 的垂线
的垂线 、
、 ,垂足分别为
,垂足分别为 、
、 ,记
,记 ,求
,求 的取值范围.
的取值范围.
4.已知函数 (
( 为常数)是R上的奇函数,函数g(x)=
为常数)是R上的奇函数,函数g(x)= 是区间
是区间 上的减函数.
上的减函数.
(Ⅰ)求 的值;
的值;
(Ⅱ)若 上恒成立,求t的取值范围;
上恒成立,求t的取值范围;
(Ⅲ)讨论关于x的方程 的根的个数.
的根的个数.
3.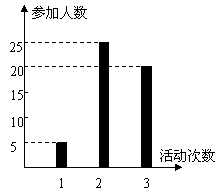 按照新课程的要求, 高中学生在每学期都要至少参加一次社会实践活
按照新课程的要求, 高中学生在每学期都要至少参加一次社会实践活
动(以下简称活动). 该校高2010级一班50名学生在上学期参加活动
的次数统计如图所示.
(I)从该班任意选两名学生,求他们参加活动次数不相等的概率 .
.
(II)从该班中任选两名学生,用 表示这两人参加活动次数之差的
表示这两人参加活动次数之差的
绝对值,求随机变量 的分布列及数学期望
的分布列及数学期望 .
.
(III)从该班中任选两名学生,用 表示这两人参加活动次数之和,
表示这两人参加活动次数之和,
记 “函数 在区间
在区间 上有且只有一个零点”为事件A,求事件A发生的概率.
上有且只有一个零点”为事件A,求事件A发生的概率.
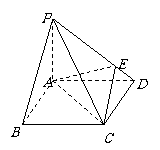
2.如图,四棱锥P-ABCD的底面是边长为 的正方形,
的正方形, ,
, ,
, ,
, 为
为 上一点,
上一点, .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求二面角 的正切值;
的正切值;
(Ⅲ)在侧棱 上是否存在一点
上是否存在一点 ,使得
,使得 ∥平面
∥平面 ,若存在,指出
,若存在,指出 点位置,并证明,若不存在,说明理由.
点位置,并证明,若不存在,说明理由.
1.若 ,其中
,其中 ,函数
,函数 且
且 的图象关于直线
的图象关于直线 对称.
对称.
(Ⅰ)求 的解析式;
的解析式;
 (Ⅱ)将
(Ⅱ)将 的图象向左平移
的图象向左平移 个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到
个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到 的图象;若函数
的图象;若函数 ,
, 的图象与
的图象与 的图象有三个交点且交点的横坐标成等比数列,求
的图象有三个交点且交点的横坐标成等比数列,求 的值.
的值.
(17)(本小题满分10分)(注意:在试题卷上作答无效)
在 中,内角A、B、C的对边长分别为
中,内角A、B、C的对边长分别为 、
、 、
、 ,已知
,已知 ,且
,且 ,
, ,求角A及
,求角A及 的面积
的面积
(18)(本小题满分12分)(注意:在试题卷上作答无效)
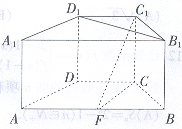 如图,在直四棱柱
如图,在直四棱柱 中,底面
中,底面 为等腰梯形,
为等腰梯形, ,
, ,
, ,
, ,
, 在棱
在棱 (不含端点)上,且
(不含端点)上,且 与底面
与底面 所成角的大小为
所成角的大小为
(Ⅰ)证明:直线 平面
平面 ;
;
(Ⅱ)求二面角 的大小
的大小
(19)(本小题满分12分)(注意:在试题卷上作答无效)
桂林某学校从参加高三年级第二次模拟考试的学生中
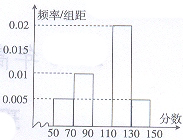 随机抽出100名学生,将其数学成绩(均为整数)分成五
随机抽出100名学生,将其数学成绩(均为整数)分成五
段 ,
, ,
, ,
, ,
,
后得到如右部分频率分布直方图,分析图形的信息,回答下
列问题:
(Ⅰ)求分数在 内的频率和学生数,并补全这
内的频率和学生数,并补全这
个频率分布直方图;
(Ⅱ)现从分数段 的学生中随机抽取2人给予助学金奖励,抽到的学生成绩在
的学生中随机抽取2人给予助学金奖励,抽到的学生成绩在 内每人奖励100元,在
内每人奖励100元,在 内每人奖励200元,在
内每人奖励200元,在 内每人奖励300元,用
内每人奖励300元,用 表示抽取结束后总的奖励金额,求
表示抽取结束后总的奖励金额,求 的分布列和数学期望
的分布列和数学期望
(20)(本小题满分12分)(注意:在试题卷上作答无效)
已知数列 满足
满足 ,
, (
( ,
, )
)
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设 (
( ),求数列
),求数列 的前
的前 项和
项和
(21)(本小题满分12分)(注意:在试题卷上作答无效)
已知 、
、 是椭圆
是椭圆 :
: (
( )的左、右焦点,
)的左、右焦点, 为坐标原点,椭圆上的点到焦点距离的最大值为
为坐标原点,椭圆上的点到焦点距离的最大值为 ,最小值为
,最小值为
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)已知⊙ 是以
是以 为直径的圆,一直线
为直径的圆,一直线 :
: 与⊙
与⊙ 相切,与椭圆
相切,与椭圆 交于不同的两点
交于不同的两点 、
、 ,且满足
,且满足 ,求
,求 面积
面积 的最大值
的最大值
(22)(本小题满分12分)(注意:在试题卷上作答无效)
已知函数 的图象在点
的图象在点 处的切线方程为
处的切线方程为 ,且在
,且在 内单调递减,在
内单调递减,在 上单调递增
上单调递增
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)若对于任意的 (
( ),不等式
),不等式 恒成立,试问这样的
恒成立,试问这样的 是否存在?若存在,求出
是否存在?若存在,求出 的范围;若不存在,请说明理由
的范围;若不存在,请说明理由
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com