(15)(本小题共12分)

　 　　 如图，在平面直角坐标系中，以轴为始边作两个锐角，它们的终边分别与单位圆交于两点．已知的横坐标分别为．

(Ⅰ)求的值；

(Ⅱ)求的值．

(16)(本小题共14分)

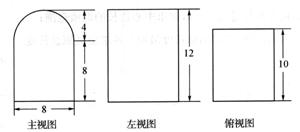
正方体的棱长为，是与的交点，是上一点，且．

(Ⅰ)求证：平面；

(Ⅱ)求异面直线与所成角的余弦值；

(Ⅲ)求直线与平面所成角的正弦值．

(17)(本小题共13分)

某学校高一年级开设了五门选修课．为了培养学生的兴趣爱好，要求每个学生必须参加且只能选修一门课程．假设某班甲、乙、丙三名学生对这五门课程的选择是等可能的．

(Ⅰ)求甲、乙、丙三名学生参加五门选修课的所有选法种数；

(Ⅱ)求甲、乙、丙三名学生中至少有两名学生选修同一门课程的概率；

(Ⅲ)设随机变量为甲、乙、丙这三名学生参加课程的人数，求的分布列与数学期望．

(18)(本小题共14分)

设函数()．

(Ⅰ)当时，求的极值；

(Ⅱ)当时，求的单调区间.

(19)(本小题共14分)

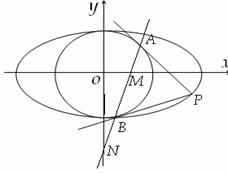
已知椭圆和圆：，过椭圆上一点引圆的两条切线，切点分别为．

(Ⅰ)(ⅰ)若圆过椭圆的两个焦点，求椭圆的离心率；

　　 (ⅱ)若椭圆上存在点，使得，求椭圆离心率的取值范围；

(Ⅱ)设直线与轴、轴分别交于点，，求证：为定值．

(20)(本小题共13分)

设集合，对于，记且，由所有组成的集合设为．

(Ⅰ)求的值；

(Ⅱ)设集合，对任意，试求；

(Ⅲ)设，试求的概率．

(考生务必将答案答在答题卡上，在试卷上作答无效)

崇文区2009－2010学年度第二学期统一练习(二)

(9)函数的定义域为　　　　　　　　　 ．

(10)如图，⊙中的弦与直径相交于　　

点，为延长线上一点，为

⊙的切线，为切点，若，

，，，

则　　　 　　　　 ．

(11)甲、乙、丙三名射击运动员在某次测试中各射击20次，三人的测试成绩如下表

分别表示甲、乙、丙三名运动员这次测试成绩的平均数，则的大小关系为　　　　 　　　　 ；分别表示甲、乙、丙三名运动员这次测试成绩的标准差，则的大小关系为　　　 　　　　 ．

(12)若直线的参数方程为(为参数)，则直线的斜率为　　　　　　　　　 ；

在极坐标系中，直线的方程为，则点到直线的距离为　　　　______．

(13)给定下列四个命题：

①若，则；

②已知直线，平面为不重合的两个平面．若，且，则∥；

③若成等比数列，则；

④若，则．

其中为真命题的是　　　　　　　　　 ．(写出所有真命题的序号)

(14)设不等式组，所表示的平面区域的整点个数为，则

　　　 　　　　 ．

(1)“关于的不等式的解集为”是“”

(A)充分非必要条件　　　　　　　　　 (B)必要非充分条件

(C)充分必要条件　　　　　　　　　　 (D)既非充分又非必要条件

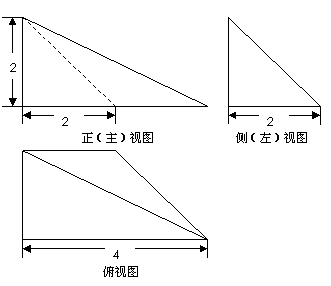(2)一个几何体的三视图如图所示，则这个几何体的体积等于

(A) 　　　　　　　(B) 　　　　　　　(C)　 　　　(D)

(3)设函数若，，则

　　 　(A) 　　　　　　　(B)　 0　 　　　　　(C)1　　　 　　(D)2

(4)把函数的图象上所有的点向左平移个单位长度，再把所得图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)，得到的图象所表示的函数为

(A)　　　　　　 (B)　　

(C)　　　　 　　(D)

(5)已知点是抛物线上的一个动点，则点到点的距离与点到该抛物线准线的距离之和的最小值为

(A)3　　　　　 (B)　　　 　(C)　 　　 　(D)

(6)若非零向量满足，则

(A) 　　　　　　　　　　(B) 　

(C)　 　　　　　　　　　(D)

(7)用5，6，7，8，9组成没有重复数字的五位数，其中恰好有一个奇数夹在两个偶数之

间的五位数的个数为

(A)120　　　　 (B)72　　　　　 (C)48　　　　 (D)36

(8)已知圆的方程，过作直线与圆交于点，且关于直线对称，则直线的斜率等于

(A) 　　　　(B)　　 　 　　(C)　 　　　(D)

崇文区2009－2010学年度第二学期统一练习(二)

　 　 　　　高三数学(理科)　　　 2010.5

第Ⅱ卷(共110分)

20.(本小题共14分)

已知，动点到定点的距离比到定直线的距离小.

(I)求动点的轨迹的方程；

(Ⅱ)设是轨迹上异于原点的两个不同点，,求面积的最小值；

(Ⅲ)在轨迹上是否存在两点关于直线对称？若存在，求出直线 的方程，若不存在，说明理由.

北京市宣武区2009~2010学年度第二学期第二次质量检测

19. (本小题共14分)

已知函数.

(I)判断函数的单调性；

(Ⅱ)若+的图像总在直线的上方，求实数的取值范围；

(Ⅲ)若函数与的图像有公共点，且在公共点处的切线相同，求实数的值.

18. (本小题共13分)

　　 设是正数组成的数列，其前项和为，且对于所有的正整数,有．

　(I) 求，的值；

　 (II) 求数列的通项公式；

　(III)令，，()，求数列的前 项和．

17. (本小题共13分)

在一次考试中共有8道选择题，每道选择题都有4个选项，其中有且只有一个选项是正确的.某考生有4道题已选对正确答案，其余题中有两道只能分别判断2个选项是错误的，还有两道题因不理解题意只好乱猜.

(Ⅰ) 求该考生8道题全答对的概率；

(Ⅱ)　

若评分标准规定：“每题只选一个选项，选对得5分，不选或选错得0分”，求该考生所得分数的分布列.

16. (本小题共13分)

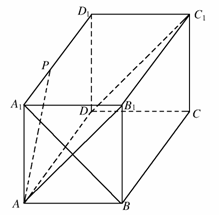
已知某个几何体的三视图如图(主视图的弧线是半圆)，根据图中标出的数据，

(Ⅰ)求这个组合体的表面积；

(Ⅱ)若组合体的底部几何体记为，其中为正方形.

(i)求证：；

(ii)设点为棱上一点，求直线与平面所成角的正弦值的取值范围.

15.(本小题共13分)

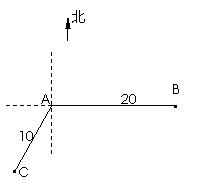如图，当甲船位于处时获悉，在其正东方向相距20海里的处有一艘渔船遇险等待营救．甲船立即前往救援，同时把消息告知在甲船的南偏西30，相距10海里处的乙船.

(Ⅰ)求处于处的乙船和遇险渔船间的距离；

(Ⅱ)设乙船沿直线方向前往处救援，其方向与成角，

求的值域.

14. 以直角坐标系的原点为极点，轴正半轴为极轴建立极坐标系，有下列命题：

①与曲线无公共点；

②极坐标为 (，)的点所对应的复数是-3+3i；

③圆的圆心到直线的距离是；

④与曲线相交于点,则点坐标是.

其中假命题的序号是　　 .