
18.解:(Ⅰ)由题意,区域U内共有 个整点
个整点 ,区域V内共有
,区域V内共有 个整点,设所取3个整点中恰有2个整点在区域V的
个整点,设所取3个整点中恰有2个整点在区域V的 概率为
概率为 ,则
,则 .…………6分
.…………6分
(Ⅱ)区域U的面积为8,区域V的面积为4,
∴在区域U内任取一点,该点在区域V内的概率为 .…………8分
.…………8分
X的取值为0,1,2,3.…………9分
 ,
,  ,
,
 ,
,  .…………11分
.…………11分
∴X的分布列为
|
X |
0 |
1 |
2 |
3 |
 |
 |
 |
 |
 |
 .…………13分
.…………13分
17.证明:(Ⅰ)由题 设
设

 ,
,
连结 ,
, 为等腰直角三角形,所以
为等腰直角三角形,所以 ,
,
且 ,又
,又 为等腰三角形,故
为等腰三角形,故 ,…………3分
,…………3分
且 ,从而
,从而 =
= .
.
所以
 为直角三角形,
为直角三角形, .
.
又 .所以
.所以 平面
平面 .…………6 分
.…………6 分
(Ⅱ)以 为坐标原点,射线
为坐标原点,射线 ,OS分别为
,OS分别为 轴、
轴、
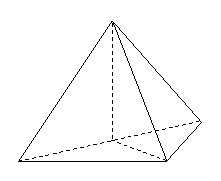
 轴,z轴的正半轴,
轴,z轴的正半轴, 建立空间直角坐标系
建立空间直角坐标系 .
.
设 ,则
,则 .
.
平面BCS的法向量 = ( 0, 1, 0 )
= ( 0, 1, 0 )
平面ACS的法向量 = ( -1, 1, 1 ) …………10分
= ( -1, 1, 1 ) …………10分
∣COS< ,
,
 >∣ = ∣
>∣ = ∣ ∣=
∣= 
所以二面角 的余弦值为
的余弦值为 .…………13分
.…………13分
16.解:(Ⅰ)把 图像上各点的横坐标伸长为原来的2倍,
图像上各点的横坐标伸长为原来的2倍,
得到 的图像,…………3分
的图像,…………3分
把得到的函数图像向左平移 ,得到
,得到 图像,
图像,
所以  …………6分
…………6分
(Ⅱ)当 时,
时, ,
, …………8分
…………8分

 ,
,
 ,则
,则 ;…………9分
;…………9分
当 时,
时, ,
, …………11分
…………11分

 ,
,
 ,则
,则 …………12分
…………12分
因此, 在区间
在区间 上的值域为
上的值域为 …………13分
…………13分
CBAAC DAADB
二 、填空题:本大题共5小题,每小题4分,共20分.
、填空题:本大题共5小题,每小题4分,共20分.
11. y-2x+1=0 12.
10 13. 2 14.  15.
45°或135°
15.
45°或135°
21.本题有(1)、(2)、(3)三个选考题,每题7分,请考生任选2题作答,满分14分.如果多做,则按所做的前两题计分.
(1) (本小题满分7分) 选修4-2:矩阵与变换
选修4-2:矩阵与变换
已知矩阵 ,其中
,其中 R,若点P(1,1)在矩阵A的变换下得到点P′(0,-3),求矩阵A的特征值及特征向量.
R,若点P(1,1)在矩阵A的变换下得到点P′(0,-3),求矩阵A的特征值及特征向量.
(2) (本小题满分7分)选修4-4:坐标系与参数方程
已知极坐标系的极点在直角坐标系的原点 处,极轴与
处,极轴与 轴的正半轴重合.直线l的极坐标方程为
轴的正半轴重合.直线l的极坐标方程为 ,圆
,圆 的参数方程为
的参数方程为 (参数
(参数 ),求圆心
),求圆心 到直线
到直线 的距离.
的距离.
(3)(本小题满分7分)选修 ;不等式选讲
;不等式选讲
已知 为正实数,且
为正实数,且 ,求
,求 的最小值及取得最小值时
的最小值及取得最小值时 的值.
的值.
2010年南平市高中毕业班适应性考试
理科数学试题参考解答及评分标准
20.(本题满分14分)
已知函数 的定义域为
的定义域为 .
.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)探究 是否是
是否是 上的单调函数?若是,请证明;若不是,请说明理由;
上的单调函数?若是,请证明;若不是,请说明理由;
(Ⅲ)求证: ,
, (其中
(其中 为自然对数的底数).
为自然对数的底数).
19.(本题满分13分)
已知抛物线C的方程为 ,A,B是抛物线C上的两点,直线AB过点M
,A,B是抛物线C上的两点,直线AB过点M 。
。
(Ⅰ)设 是抛物线上任意一点,求
是抛物线上任意一点,求 的最小值;
的最小值;
(Ⅱ)求向量 与向量
与向量 的夹角(O是坐标原点);
的夹角(O是坐标原点);
(Ⅲ)在 轴上是否存在异于M的一点N,直线AN与抛物线的另一个交点为D,而直线DB与
轴上是否存在异于M的一点N,直线AN与抛物线的另一个交点为D,而直线DB与 轴交于点E,且有
轴交于点E,且有 ?若存在,求出N点坐标;若不存在,说明理由.
?若存在,求出N点坐标;若不存在,说明理由.
18.(本小题满分13分)
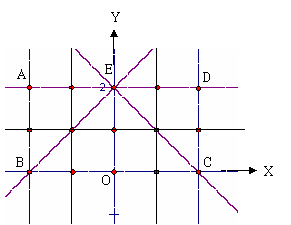
 设不等式组
设不等式组 确定的平面区域为U,
确定的平面区域为U,
 确定的平面区域为V.
确定的平面区域为V.
(Ⅰ)定义坐标为整数的点为“整点”.在区域U内任取3个整点,求这些整点中恰有2个整点在区域V的概率;
(Ⅱ)在区域U内任取3个点,记此3个点在区域V的个数为X,求X的概率分布列及其数学期望.
17.(本小题满分13分)
如图,在三棱锥 中,侧面
中,侧面 与侧面
与侧面 均为等边三角形,
均为等边三角形, ,
, 为
为 中点.
中点.
(Ⅰ)证明: 平面
平面 ;
;
(Ⅱ)求二面角 的余弦值.
的余弦值.
16.(本题满分13分)设函数 ,
, ,
,
(Ⅰ)如果函数 的图像是由函数
的图像是由函数 的图像上各点
的图像上各点 的横坐标伸长为原来的2倍,再把所得图像向左平移
的横坐标伸长为原来的2倍,再把所得图像向左平移 得到,求函数
得到,求函数 解析式;
解析式;
(Ⅱ)如果 ,求
,求 在区间
在区间 上的值域.
上的值域.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com