
6、在直三棱柱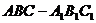 中,
中,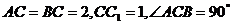 ,
,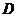 在
在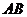 上,且
上,且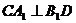 ,如果以射线
,如果以射线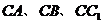 为
为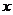 轴、
轴、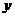 轴、
轴、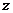 轴建立空间直角坐标系,求
轴建立空间直角坐标系,求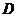 点的坐标。
点的坐标。
答案见《突破课堂》P62巩固练习8
5、已知点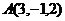 ,点
,点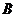 在
在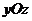 平面内,直线
平面内,直线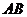 的方向向量是
的方向向量是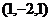 ,求
,求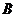 点坐标。
点坐标。
答案见《突破课堂》P59课堂反馈6
4、平面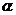 的法向量
的法向量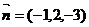 ,点
,点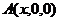 在
在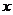 轴上,点
轴上,点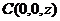 在
在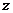 轴上,
轴上,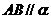 ,则
,则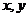 之间的数量关系式是?
之间的数量关系式是?
答案见《突破课堂》P64巩固练习5
3、两个平面的法向量互相垂直,这两个法向量分别是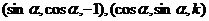 ,其中
,其中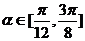 ,则
,则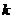 的取值范围是?
的取值范围是?
答案见《突破课堂》P61巩固练习3
2、在空间直角坐标系中,过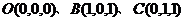 三点平面的法向量是?
三点平面的法向量是?
答案见《突破课堂》P60巩固练习5
1、设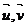 分别是平面α,β的法向量,根据下列条件,判断α,β的位置关系.
分别是平面α,β的法向量,根据下列条件,判断α,β的位置关系.
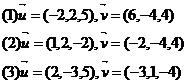
答案:(1)垂直(2)平行(3)相交
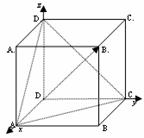 例1:在正方体
例1:在正方体 中,求证:
中,求证: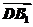 是
是
平面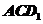 的法向量
的法向量
证:设正方体棱长为1,
以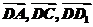 为单位正交基底,建立如图所示空间坐标系
为单位正交基底,建立如图所示空间坐标系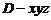 ,则A(1,0,0),
,则A(1,0,0),
C(0,1,0),D1(0,0,1),B1(1,1,1)
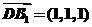 ,
,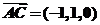 ,
,
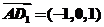
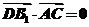 ,
,
所以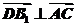 ,同理
,同理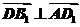
又因为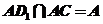
所以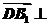 平面
平面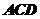 ,从而
,从而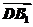 是平面
是平面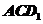 的一个法向量.
的一个法向量.
例2、在空间直角坐标系内,设平面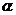 经过点
经过点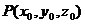 ,平面
,平面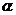 的法向量为
的法向量为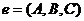 ,
,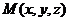 是平面
是平面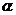 内任意一点,求
内任意一点,求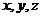 满足的关系式。
满足的关系式。
答案见课本P89
例3、证明:在平面内的一条直线,如果它和这个平面的一条斜线在这个平面内的射影垂直,那么它也和这条斜线垂直。(三垂线定理)
答案见课本P90
例4、证明:如果一条直线和平面内的两条相交直线垂直,那么这条直线垂直于这个平面。(直线与平面垂直的判定定理)
答案见课本P91
例5、如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=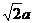 ,点E是PD的中点.证明:PA⊥平面ABCD,PB∥平面EAC.
,点E是PD的中点.证明:PA⊥平面ABCD,PB∥平面EAC.
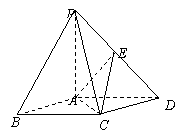
证明:先证明PA⊥平面ABCD.
建立空间直角坐标系A-xyz,则
A(0,0,0),B(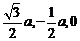 ),D(0,a,0),P(0,0,a),于是,
),D(0,a,0),P(0,0,a),于是,
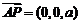 ,
,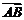 =(
=(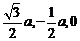 ),
),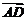 =(0,a,0).
=(0,a,0).
∵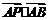 =0+0+0=0,
=0+0+0=0,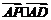 =0+0+0=0,
=0+0+0=0,
∴AP⊥AB,AP⊥AD.
∵AB、AD为平面ABCD内的两相交直线,
∴AP⊥平面ABCD.
再证明PB∥平面EAC.
因为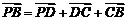
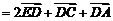
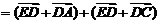
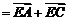 ,
,
所以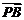 、
、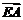 、
、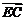 共面.
共面.
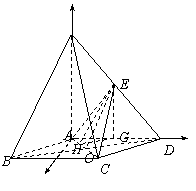 又PBË平面EAC,所以PB∥平面EAC.
又PBË平面EAC,所以PB∥平面EAC.
2、平面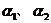 的法向量分别是
的法向量分别是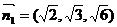 ,
,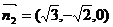 ,则平面
,则平面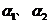 的位置关系是?
的位置关系是?
答案见《突破课堂》P61课堂反馈4
1、平面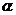 经过原点
经过原点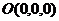 ,法向量
,法向量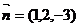 ,
,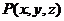 是
是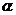 内的一点,则
内的一点,则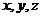
满足的数量关系是?
答案见《突破课堂》P59课堂反馈3
2、设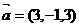 ,
,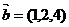 ,若
,若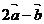 与
与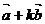 互相垂直,则实数
互相垂直,则实数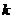 的值是?
的值是?
答案见《突破课堂》P61课堂反馈1
c. 预习提高题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com