
16、向量:既有大小,又有方向的量.
数量:只有大小,没有方向的量.
有向线段的三要素:起点、方向、长度.
零向量:长度为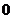 的向量.
的向量.
单位向量:长度等于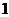 个单位的向量.
个单位的向量.
平行向量(共线向量):方向相同或相反的非零向量.零向量与任一向量平行.
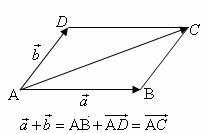
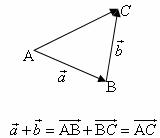 相等向量:长度相等且方向相同的向量.
相等向量:长度相等且方向相同的向量.
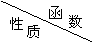
15、正弦函数、余弦函数和正切函数的图象与性质:
 |
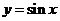 |
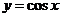 |
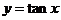 |
|
图象 |
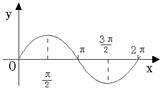 |
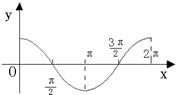 |
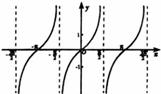 |
|
定义域 |
 |
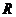 |
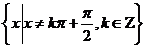 |
|
值域 |
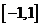 |
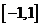 |
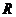 |
|
最值 |
当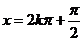 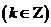 时, 时,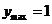 ;当 ;当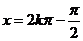 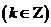 时, 时,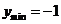 . . |
当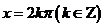 时, 时, 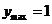 ;当 ;当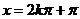 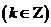 时, 时,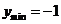 . . |
既无最大值也无最小值 |
|
周期性 |
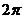 |
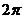 |
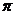 |
|
奇偶性 |
奇函数 |
偶函数 |
奇函数 |
|
单调性 |
在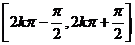 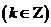 上是增函数;在 上是增函数;在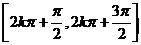 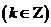 上是减函数. 上是减函数. |
在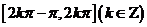 上是增函数;在 上是增函数;在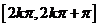 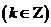 上是减函数. 上是减函数. |
在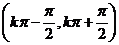 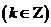 上是增函数. 上是增函数. |
|
对称性 |
对称中心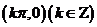 对称轴 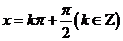 |
对称中心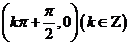 对称轴 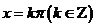 |
对称中心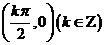 无对称轴 |
14、函数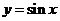 的图象上所有点向左(右)平移
的图象上所有点向左(右)平移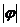 个单位长度,得到函数
个单位长度,得到函数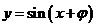 的图象;再将函数
的图象;再将函数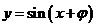 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的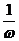 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数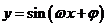 的图象;再将函数
的图象;再将函数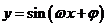 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的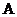 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数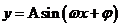 的图象.
的图象.
函数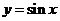 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的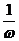 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数
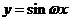 的图象;再将函数
的图象;再将函数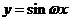 的图象上所有点向左(右)平移
的图象上所有点向左(右)平移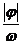 个单位长度,得到函数
个单位长度,得到函数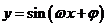 的图象;再将函数
的图象;再将函数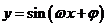 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的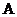 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数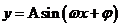 的图象.
的图象.
函数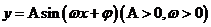 的性质:
的性质:
①振幅: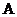 ;②周期:
;②周期: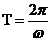 ;③频率:
;③频率: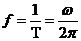 ;④相位:
;④相位: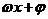 ;⑤初相:
;⑤初相: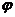 .
.
函数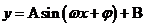 ,当
,当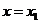 时,取得最小值为
时,取得最小值为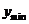 ;当
;当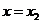 时,取得最大值为
时,取得最大值为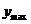 ,则
,则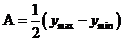 ,
,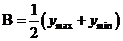 ,
,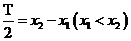 .
.
13、三角函数的诱导公式:
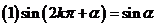 ,
,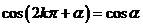 ,
,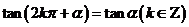 .
.
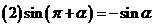 ,
,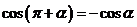 ,
,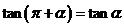 .
.
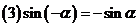 ,
,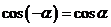 ,
,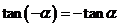 .
.
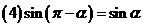 ,
,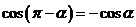 ,
,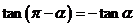 .
.
口诀:函数名称不变,符号看象限.
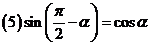 ,
,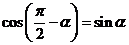 .
.
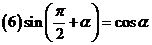 ,
,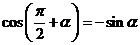 .
.
口诀:正弦与余弦互换,符号看象限.
12、同角三角函数的基本关系: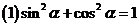
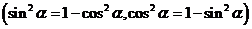 ;
;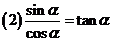
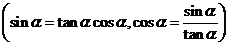 .
.
11、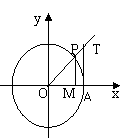 三角函数线:
三角函数线: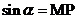 ,
,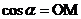 ,
,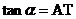 .
.
10、三角函数在各象限的符号:第一象限全为正,第二象限正弦为正,第三象限正切为正,第四象限余弦为正.
9、设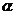 是一个任意大小的角,
是一个任意大小的角,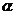 的终边上任意一点
的终边上任意一点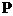 的坐标是
的坐标是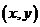 ,它与原点的距离是
,它与原点的距离是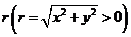 ,则
,则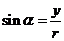 ,
,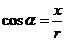 ,
,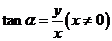 .
.
8、若扇形的圆心角为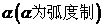 ,半径为
,半径为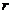 ,弧长为
,弧长为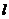 ,周长为
,周长为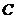 ,面积为
,面积为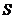 ,则
,则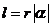 ,
,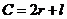 ,
,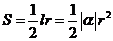 .
.
7、弧度制与角度制的换算公式: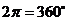 ,
,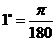 ,
,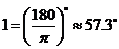 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com