5．C．f(x)= -x²+2ax 对称轴为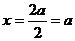在[1,2]上是减函数　 ∴a≤1

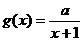在[1,2]上减函数，则a>0

∴0<a≤1

4．D．令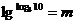 则

　　　 ∴

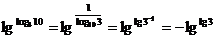
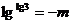
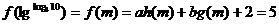　　　 　　∴ah(m)+bg(m)=3

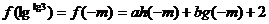
=-ah(m)-bg(m)+2

=-1

3．C．x²=1　 ∴x=±1;　 x²=4　 ∴x=±2

定义域中只有两个元素数组有(1,2)(-1,2), (1,-2)(-1,-2)

定义域中有三个元素的数组有(1,-1,2)(-1,-1,-2), (1,2,-2), (-1,2,2)

定义域中有四个元素有(1,-1,2,-2)

∴共9个

2．C．y=log₂x, ∴x=2^y　 ∴f^-1(x)=2^x　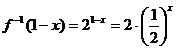 ∴, x=0, f^-1(1-x)=2

　　　 x=1, f^-1(1-x)=1，用特殊值即可知选C。

1．A．f(2+t)=f(2-t),　 ∴y=f(x)关于x=2对称，根据对称性可得。

10．某种商品定价为每件60元,不加收附加税时每年大约销售80万件,若政府征收附加税，每销售100元要征税p元(即税率为p%)，因此每年销售量将减少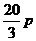万件。

　　 (1)将政府每年对该商品征收的总税金y(万元)，表示成P的函数、并指出这个函数的定义域。

　　 (2)要使政府在此项经营中每年收取的税金不少于128万元,问税率p%应怎样确定?

　　 (2)在所收税金不少于128万元的前提下，要让厂家获得最大的销售金额，则应如何确定p值。

函数图象性质(一)答案

9．已知关于x的方程：9^x+a·3^x+a+1=0有两个不等实根，求实数a的值。

8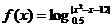．的单调递增区间是　　　　　　　　　　　　　　　　 。

7．函数y=lg(x²+2x+a)定义域为R，实数a取值范围是　　　　　 　　 　　　 值域为R，实数a的取值范围是　　　　 　　　　 。

6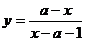．的图象关于点(4,-1)对称，则函数a=　　　　　　　　　　　　　　　 。