
1.若θ∈(0,2π],则使sinθ<cosθ<cotθ<tanθ成立的θ取值范围是( C )
(A)(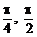 ) (B)(
) (B)(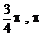 )(C)(
)(C)(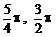 ) (D)(
) (D)(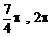 )
)
5.设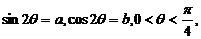 给出
给出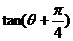 值的四个答案:
值的四个答案:
①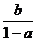 ;②
;②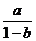 ;③
;③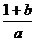 ;④
;④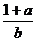 .其中正确的是
①④.
.其中正确的是
①④.
6.已知函数f(x)=-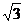 sin2x+sinxcosx.
sin2x+sinxcosx.
(Ⅰ) 求f(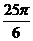 )的值; (Ⅱ) 设
)的值; (Ⅱ) 设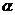 ∈(0,
∈(0,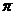 ),f(
),f(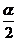 )=
)=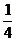 -
-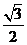 ,求sin
,求sin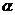 的值.
的值.
[专家解答](Ⅰ) 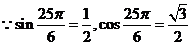
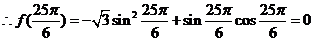
(Ⅱ) 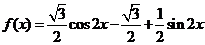 ,
,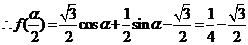
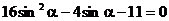 解得
解得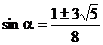
★★★高考要考什么
[考点透视]
本专题主要涉及同角三角函数基本关系,诱导公式,两角和差公式,倍角公式,升幂缩角、降幂扩角公式等公式的应用.
[热点透析]
三角函数式的化简和求值是高考考查的重点内容之一 通过本节的学习使考生掌握化简和求值问题的解题规律和途径,特别是要掌握化简和求值的一些常规技巧,以优化我们的解题效果,做到事半功倍
通过本节的学习使考生掌握化简和求值问题的解题规律和途径,特别是要掌握化简和求值的一些常规技巧,以优化我们的解题效果,做到事半功倍
★★★突破重难点
[范例1]设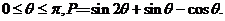
(1) 若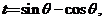 用含
用含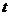 的式子表示
的式子表示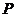 ;
;
(2) 确定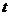 的取值范围,并求出
的取值范围,并求出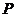 的最大值.
的最大值.
解析(1)由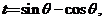 有
有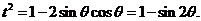
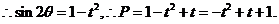
(2)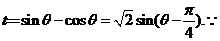
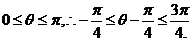
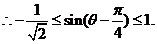 即
即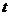 的取值范围是
的取值范围是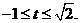
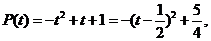 在
在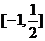 内是增函数,在
内是增函数,在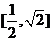 内是减函数.
内是减函数.
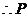 的最大值是
的最大值是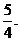
[点晴]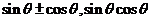 间通过平方可以建立关系,“知其一,可求其二”.
间通过平方可以建立关系,“知其一,可求其二”.
[文]已知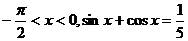 .
.
(I)求sinx-cosx的值;
(Ⅱ)求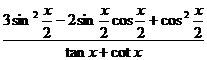 的值.
的值.
解析:法1(Ⅰ)由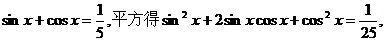
即 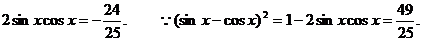
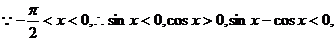 故
故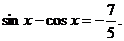
(Ⅱ)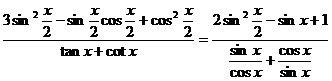
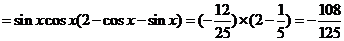
|
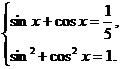
由①得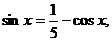 将其代入②,整理得
将其代入②,整理得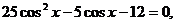
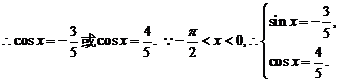 故
故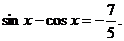
(Ⅱ)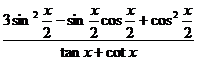
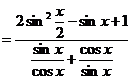
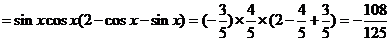
[点晴]此题主要考查三角函数的基本公式、三角恒等变换、三角函数在各象限符号等基本知识,以及推理和运算能力.
[范例2]已知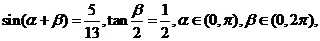
(1) 求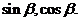 求
求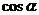 .
.
解析:(1)由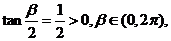 则
则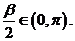
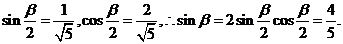
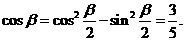
(2)由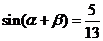 知
知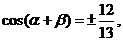
由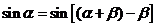
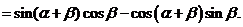
在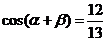 时,
时,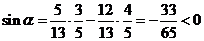 与
与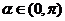 矛盾,舍去.
矛盾,舍去.
在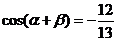 时,
时,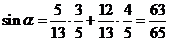 可取.因此
可取.因此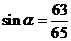 .
.
[点晴]在求值时,要注意用已知角来表示所求角,讲究拆角、配角技术。
[文]已知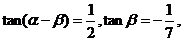 且
且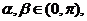 求
求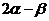 的值.
的值.
解: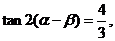
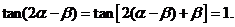
由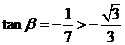 知
知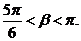
由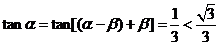 知
知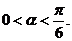
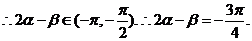
[点睛]如果要求解的角是由一些表达式给出的,则一是考虑所求解的角与已知条件中的角的关系,尽量将所求解的角用已知条件中的角表示出来;二是考虑求该角的某个三角函数值,具体哪个三角公式,一般可由条件中的函数去确定,一般已知正切函数值,选正切函数.已知正、余弦函数值时,选正、余弦函数。若角范围是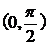 ,正、余弦函数均可,若角是
,正、余弦函数均可,若角是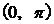 时,一般选余弦函数,若是
时,一般选余弦函数,若是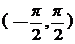 时,则一般选正弦函数。
时,则一般选正弦函数。
[范例3]已知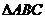 的面积S 满足
的面积S 满足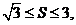 且
且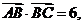
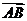 与
与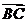 的夹角为
的夹角为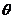 .
.
(1) 求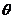 的取值范围;
的取值范围;
(2) 求函数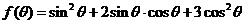 的最小值.
的最小值.
解析 (1)由题意知,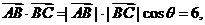 ①
①
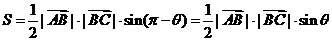 ②
②
由②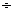 ①,得
①,得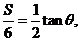 即
即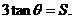 由
由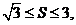 得
得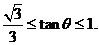
又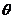 为
为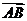 与
与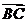 的夹角,
的夹角,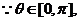
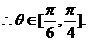
(2)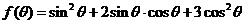
=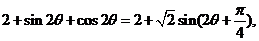
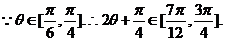
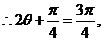 即
即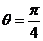 时,
时,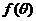 的最小值为3
的最小值为3
[点睛]本题体现了三角函数与平面向量的灵活应用。
[变式]已知向量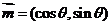 和
和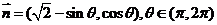 且
且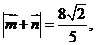 求
求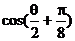 的值.
的值.
解析 法1: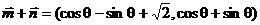
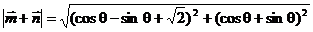

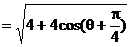

由已知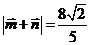 ,得
,得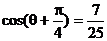
又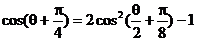
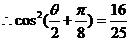
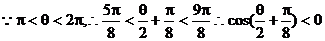
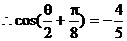
法2: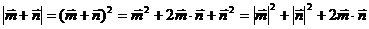
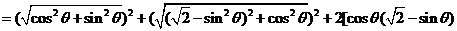
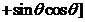
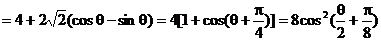
由已知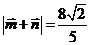 ,得
,得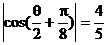
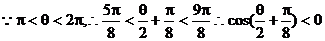
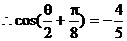
[点睛]解决此题的关键是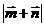 的计算,有两种途径,其解法二的运算量较小,由此得到的结果,找出与
的计算,有两种途径,其解法二的运算量较小,由此得到的结果,找出与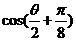 的联系。
的联系。
[范例4]设关于x的函数y=2cos2x-2acosx-(2a+1)的最小值为f(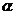 ),试确定满足f(
),试确定满足f(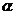 )=
)=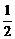 的a值,并对此时的a值求y的最大值
的a值,并对此时的a值求y的最大值
解析 由y=2(cosx-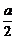 )2-
)2-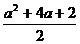 及cosx∈[-1,1]得
及cosx∈[-1,1]得
f(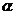 )=
)=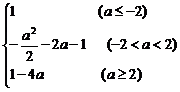
∵f (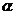 )=
)=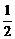 ,
,
∴1-4a=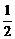
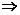 a=
a=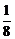
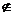 [2,+∞
[2,+∞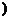 或-
或-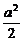 -2a-1=
-2a-1=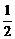 ,解得a=-1
,解得a=-1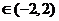 ,
,
此时,y=2(cosx+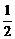 )2+
)2+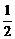 ,当cosx=1时,即x=2kπ,k∈Z,ymax=5
,当cosx=1时,即x=2kπ,k∈Z,ymax=5
[点晴] 此题三角函数与二次函数的综合应用
[变式]已知f(x)=2asin2x-2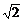 asinx+a+b的定义域是[0,
asinx+a+b的定义域是[0,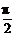 ],值域是[-5,1],求a、b的值.
],值域是[-5,1],求a、b的值.
解析 令sinx=t,∵x∈[0,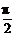 ],∴t∈[0,1],
],∴t∈[0,1],
f(x)=g(t)=2at2-2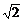 at+a+b=2a(t-
at+a+b=2a(t-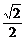 )2+b.
)2+b.
当a>0时,则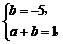 解之得a=6,b=-5.
解之得a=6,b=-5.
当a<0时,则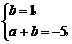 解之得a=-6,b=1.
解之得a=-6,b=1.
[点睛]注意讨论的思想
★★★自我提升
4.△ABC中,若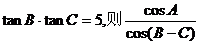 的值为
的值为
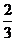 .
.
3. 在△OAB中,O为坐标原点,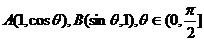 ,则当△OAB的面积达最大值时,
,则当△OAB的面积达最大值时,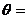 ( D
)
( D
)
(A)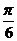 (B)
(B)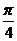 (C)
(C)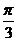 (D)
(D)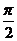
1.若 且同时满足
且同时满足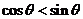 和
和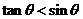 ,那么角θ的取值范围是( A
)
,那么角θ的取值范围是( A
)
(A)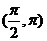 (B)
(B)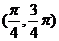 (C)
(C)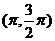 (D)
(D)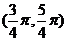
2.函数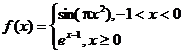 ,若
,若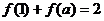 ,则
,则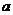 的所有可能值为
的所有可能值为
( B )
(A)1
(B)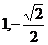 (C)
(C)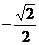 (D)
(D)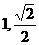
8.(理)过P(1,0)做曲线C:y=xk(xÎ(0,+¥),kÎN+,k>1)的切线,切点为Q1,设Q1在x轴上的投影为P1,又过P1做曲线C的切线,切点为Q2,设Q2在x轴上的投影为P2,…,依次下去得到一系列点Q1、Q2、Q3、…、Qn的横坐标为an,求证:
(Ⅰ)数列{an}是等比数列;
(Ⅱ)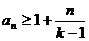 ;
;
(Ⅲ)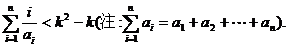
解:(Ⅰ)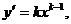 若切点是
若切点是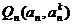 ,
,
则切线方程为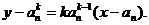
当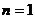 时,切线过点P(1,0)即
时,切线过点P(1,0)即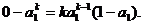 得
得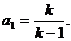
当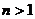 时,切线过点
时,切线过点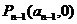 即
即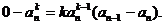 得
得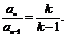
∴数列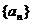 是首项为
是首项为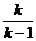 ,公比为
,公比为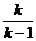 的等比数列.
的等比数列.  …6分
…6分
(Ⅱ)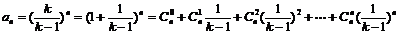
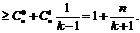
(Ⅲ)记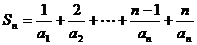 ,
,
则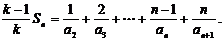
两式相减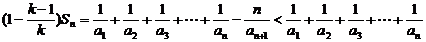
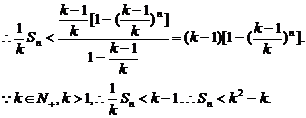
(文)已知曲线C:xy=1,过C上一点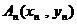 作一斜率为
作一斜率为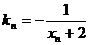 的直线交曲线C于另一点
的直线交曲线C于另一点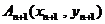 ,点列
,点列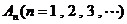 的横坐标构成数列{
的横坐标构成数列{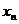 },其中
},其中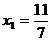 .
.
(1)求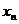 与
与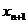 的关系式; (2)求证:{
的关系式; (2)求证:{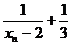 }是一等比数列.
}是一等比数列.
解析:(1)过C: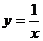 上一点
上一点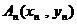 作斜率为
作斜率为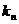 的直线交C于另一点
的直线交C于另一点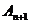 ,
,
则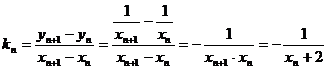 ,于是
,于是 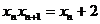 .
.
(2)记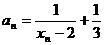 ,则
,则
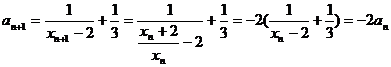 ,
,
因为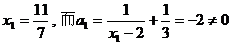 ,
,
因此数列{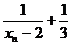 }是等比数列.
}是等比数列.
7. (理) 已知x轴上有一点列:P1(x1,0), P2(x2,0), …,Pn(xn,0),…点Pn+2 分有向线段
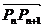 所成的比为λ,其中n∈N*,λ>0为常数,x1=1, x2=2.
所成的比为λ,其中n∈N*,λ>0为常数,x1=1, x2=2.
(1)设an=xn+1-xn,求数列{a n}的通项公式;
(2)设f (λ)=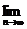 x n,当λ变化时,求f (λ)的取值范围.
x n,当λ变化时,求f (λ)的取值范围.
解析 (1)由题得 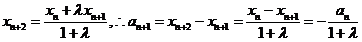
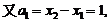 ∴{an}是首项为1,公比为
∴{an}是首项为1,公比为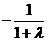 的等比数列,
的等比数列,
∴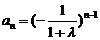
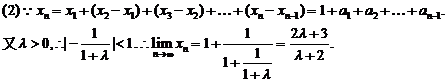
∴当λ>0时 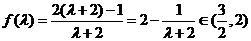
(文) 设曲线与一次函数y=f(x)的图象关于直线 y=x对称,若f (-1)=0,且点 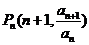 在曲线上,又a1= a2.
在曲线上,又a1= a2.
(1)求曲线C所对应的函数解析式;
(2)求数列{a n}d的通项公式.
解析:(1)y=x-1 (2) a n=(n-1)!
6. 已知函数f(x) = 2x2-x,则使得数列{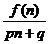 }(n∈N+)成等差数列的非零常数p与q所满足的关系式为 .p=-2q
}(n∈N+)成等差数列的非零常数p与q所满足的关系式为 .p=-2q
5. 一个机器猫每秒前进或后退一步,程序设计人员让机器猫以每前进3步,然后再后退2步的规律移动;如果将此机器猫放在数轴的原点上,面向正的方向,以1步的距离为1个单位长,令P(n)表示第n秒时机器猫所在的位置的坐标,且P(0)=0,那么下列结论中错误的是( C)
(A)P(3)=3 (B)P(5)=1 (C)P(101)=21 (D)P(103)<P(104)
4. 弹子棋共有60颗大小相同的球形弹子,现在棋盘上将它叠成正四面体形的球垛,使剩下的弹子尽可能少,那么剩余的弹子有(B)
(A)0颗 (B)4颗 (C)5颗 (D)11颗
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com