
3.抛物线y=-x2上的点到直线4x+3y-8=0距离的最小值是( A )
A.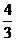 B.
B.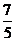 C.
C.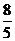 D.
D.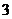
2. P是双曲线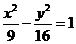 的右支上一点,M、N分别是圆(x+5)2+y2=4和(x-5)2+y2=1上的点,则|PM|-|PN|的最大值为( B )
的右支上一点,M、N分别是圆(x+5)2+y2=4和(x-5)2+y2=1上的点,则|PM|-|PN|的最大值为( B )
A. 6 B.7 C.8 D.9
1.已知双曲线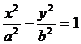 (a>0,b>0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是(C )
(a>0,b>0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是(C )
A.( 1,2)
B. (1,2)
C.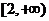 D.(2,+∞)
D.(2,+∞)
11.如图,A为椭圆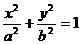
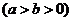 上的一个动点,弦AB、AC分别过焦点F1、F2.当AC垂直于x轴 时,恰好|AF1|:|AF2=3:1
上的一个动点,弦AB、AC分别过焦点F1、F2.当AC垂直于x轴 时,恰好|AF1|:|AF2=3:1
(I)求该椭圆的离心率;
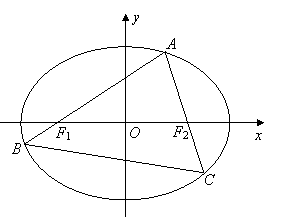 (II)设
(II)设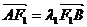 ,
,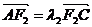 ,
,
试判断l1+l2是否为定值?若是,则求出该定
值;若不是,请说明理由.
解:(I)当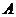 C垂直于x轴时,
C垂直于x轴时,
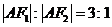 ,由
,由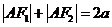 ,
,
得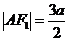 ,
,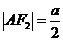
在Rt△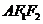 中,
中,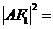
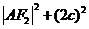
解得 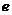 =
=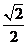 .
.
(II)由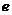 =
=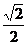 ,则
,则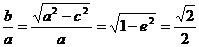 ,
,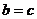 .
.
焦点坐标为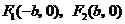 ,则椭圆方程为
,则椭圆方程为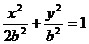 ,
,
化简有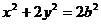 .
.
设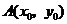 ,
,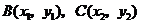 ,
,
①若直线AC的斜率存在,则直线AC方程为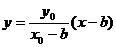
代入椭圆方程有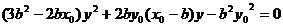 .
.
由韦达定理得: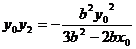 ,∴
,∴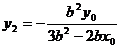
所以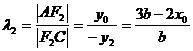 ,同理可得
,同理可得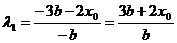
故l1+l2=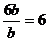 .
.
②若直线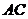
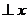 轴,
轴,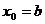 ,
,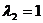 ,
,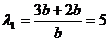
∴l1+l2=6.
综上所述:l1+l2是定值6.
10.已知椭圆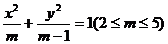 过其左焦点且斜率为1的直线与椭圆及准线从左到右依次变于A、B、C、D,设f(m)=||AB|-|CD||,(1)求f(m),(2)求f(m)的最值。
过其左焦点且斜率为1的直线与椭圆及准线从左到右依次变于A、B、C、D,设f(m)=||AB|-|CD||,(1)求f(m),(2)求f(m)的最值。
解:(1)椭圆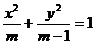 中,a2=m,b2=m-1,c2=1,左焦点F1(-1,0)
中,a2=m,b2=m-1,c2=1,左焦点F1(-1,0)
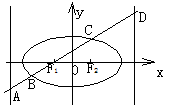 则BC:y=x+1,代入椭圆方程即(m-1)x2+my2-m(m-1)=0
则BC:y=x+1,代入椭圆方程即(m-1)x2+my2-m(m-1)=0
得(m-1)x2+m(x+1)2-m2+m=0
∴(2m-1)x2+2mx+2m-m2=0
设B(x1,y1),C(x2,y2),则x1+x2=-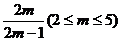
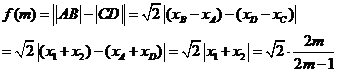 (2)
(2)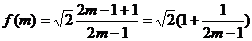
∴当m=5时,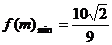 当m=2时,
当m=2时,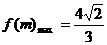
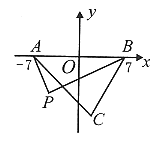
9.如图,已知三点A(-7, 0),B(7,0),C(2,-12).
① 若椭圆过A、B两点,且C为其一焦点,
求另一焦点P的轨迹方程;
② 若双曲线的两支分别过A、B两点,且C为其一
焦点,求另一焦点Q的轨迹方程。
解析:①由椭圆定义知,|AP|+|AC|=|BP|+|BC|,
即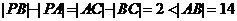
故P的轨迹为A(-7,0)、B(7,0)为焦点实轴长为2的双曲线的一支,
其方程为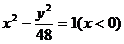 ;
;
② 经讨论知,无论A在双曲线的哪一支上,
总有|QA|+|QB|=|AC|+|BC|=28>|AB|=14
故点Q的轨迹为以A(-7,0)、B(7,0)为焦点长轴长为28的椭圆,
其方程为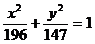 。
。
8. 已知⊙O:x2+y2=4,一动抛物线过A(-1,0)、B(1,0)两点,且以圆的切线为准线,则动抛物线的焦点F的轨迹方程为____
已知⊙O:x2+y2=4,一动抛物线过A(-1,0)、B(1,0)两点,且以圆的切线为准线,则动抛物线的焦点F的轨迹方程为____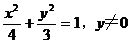
7.已知椭圆E的离心率为e,左、右焦点为F1、F2,抛物线C以F2为焦点,F1为其顶点,若P为两曲线的公共点,且e|PF2|=|PF1|,则e=__________。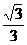
6. F1、F2是椭圆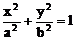 (a>b>0)的两焦点,过F1的弦AB与F2组成等腰直角三角形ABF2,其中∠BAF2=900,则椭圆的离心率是________
(a>b>0)的两焦点,过F1的弦AB与F2组成等腰直角三角形ABF2,其中∠BAF2=900,则椭圆的离心率是________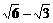
5. 已知点F1(-4,0),F2(4,0), 又P(x,y)是曲线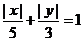 上的点, 则 (C)
上的点, 则 (C)
A. |PF1|+|PF2|=10 B. |PF1|+|PF2|<10 C. |PF1|+|PF2|£10 D. |PF1|+|PF2|³10
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com