
8.已知A、B为抛物线x2=2py (p>0)上两点,直线AB过焦点F,A、B在准线上的射影分别为C、D.
(1)若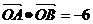 ,求抛物线的方程。
,求抛物线的方程。
(2)CD是否恒存在一点K,使得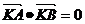
解:(1)提示:记A(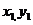 )、B (
)、B (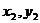 )设直线AB方程为
)设直线AB方程为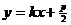 代入
代入
抛物线方程得x2-2kpx-p2=0
,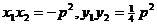
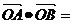
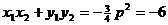
(2)设线段AB中点P在在准线上的射影为T,
则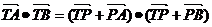
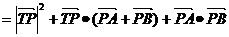
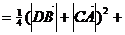
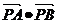 =
=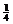
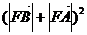 -
-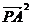 =
=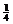
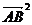 -
-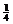
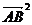 =0
=0
故存在点K即点T,使得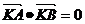
7.已知圆x2+y2=1,双曲线(x-1)2-y2=1,直线l同时满足下列两个条件:①与双曲线交于不同两点;②与圆相切,且切点是直线与双曲线相交所得弦的中点。求直线l方程。
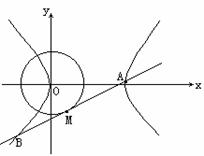 分析:选择适当的直线方程形式,把条件“l是圆的切线”“切点M是弦AB中点”翻译为关于参数的方程组。
分析:选择适当的直线方程形式,把条件“l是圆的切线”“切点M是弦AB中点”翻译为关于参数的方程组。
法一:当l斜率不存在时,x=-1满足;
当l斜率存在时,设l:y=kx+b
与⊙O相切,设切点为M,则|OM|=1
∴ 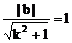 ∴ b2=k2+1 ①
∴ b2=k2+1 ①
由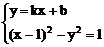 得(1-k2)x2-2(1+kb)x-b2=0
得(1-k2)x2-2(1+kb)x-b2=0
当k≠±1且△>0时,设A(x1,y1),B(x2,y2),则中点M(x0,y0),
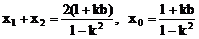 ∴ y0=kx0+b=
∴ y0=kx0+b=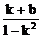
∵ M在⊙O上 ∴ x02+y02=1 ∴ (1+kb)2+(k+b)2=(1-k2)2 ②
由①②得: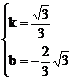 或
或 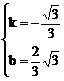 ∴
∴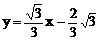 或
或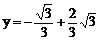
法二:设M(x0,y0),则切线AB方程x0x+y0y=1
当y0=0时,x0=±1,显然只有x=-1满足;
当y0≠0时, 代入(x-1)2-y2=1得:(y02-x02)x2+2(x0-y0)2x-1=0
代入(x-1)2-y2=1得:(y02-x02)x2+2(x0-y0)2x-1=0
∵ y02+x02=1 ∴化简方程为 (1-2x02)x2+2(x02+x0-1)x-1=0
由中点坐标公式及韦达定理得: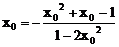
∴2x03-x02-2x0+1=0 解之得:x0=±1(舍),x0=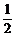 ∴ y0=
∴ y0=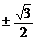 。
。
6.已知A、B为抛物线x2=2py (p>0)上两点,直线AB过焦点F,A、B在准线上的射影分别为C、D,则①y轴上恒存在一点K,使得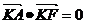 ;②
;②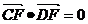 ;③存在实数l使得
;③存在实数l使得 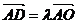 ;④若线段AB中点P在在准线上的射影为T,有
;④若线段AB中点P在在准线上的射影为T,有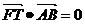 。中说法正确的为___________①②③④
。中说法正确的为___________①②③④
5、已知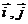 是x,y轴正方向的单位向量,设
是x,y轴正方向的单位向量,设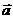 =
=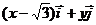 ,
, 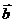 =
=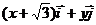 ,且满足|
,且满足|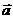 |-|
|-|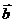 |=2.则点P(x,y)的轨迹C的方程为__________.(
|=2.则点P(x,y)的轨迹C的方程为__________.( 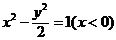 ).
).
4、直线y=kx+1与椭圆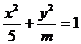 恒有公共点,则m的取值范围是(A).
恒有公共点,则m的取值范围是(A).
A、m≥1且m≠5 B、m≥1 C、m≠5 D、m≤5
3、中心在原点,焦点在坐标为(0,±5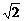 )的椭圆被直线3x-y-2=0截得的弦的中点的横坐标为
)的椭圆被直线3x-y-2=0截得的弦的中点的横坐标为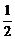 ,则椭圆方程为(C )
,则椭圆方程为(C )
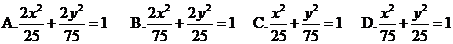
2、已知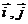 是x,y轴正方向的单位向量,设
是x,y轴正方向的单位向量,设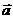 =
=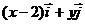 ,
, 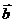 =
=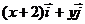 ,且满足|
,且满足|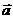 |+|
|+|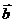 |=4.则点P(x,y)的轨迹是.( C )
|=4.则点P(x,y)的轨迹是.( C )
A.椭圆 B.双曲线 C.线段 D.射线
1、平面直角坐标系中,O为坐标原点,已知A(3,1),B(-1,3),若点C满足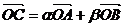 ,其中a,bÎR,且a+b=1,则点C的轨迹方程为( D )
,其中a,bÎR,且a+b=1,则点C的轨迹方程为( D )
A. 3x+2y-11=0 B.(x-1)2+(y-2)2=5 C. 2x-y=0 D. x+2y-5=0
6. 已知两定点
已知两定点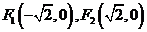 ,满足条件
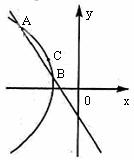
,满足条件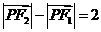 的点P的轨迹是曲线E,直线y=kx-1与曲线E交于A,B两点。如果
的点P的轨迹是曲线E,直线y=kx-1与曲线E交于A,B两点。如果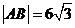 ,且曲线E上存在点C,使
,且曲线E上存在点C,使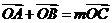 ,求m的值和DABC的面积S。
,求m的值和DABC的面积S。
[专家解答]由双曲线的定义可知,曲线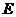 是以
是以
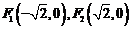 为焦点的双曲线的左支,
为焦点的双曲线的左支,
且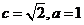 ,易知
,易知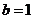 ,
,
故曲线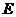 的方程为
的方程为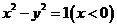
设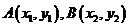 ,由方程组
,由方程组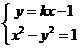
消去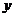 ,得
,得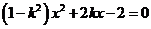
又已知直线与双曲线左支交于两点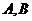 ,有
,有
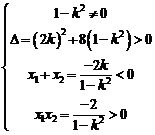 解得
解得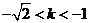
又∵ 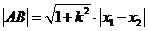
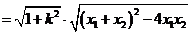
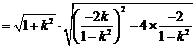
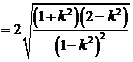
依题意得 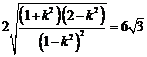 整理后得
整理后得 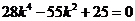
∴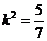 或
或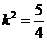 但
但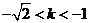 ∴
∴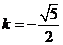
故直线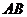 的方程为
的方程为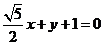
设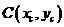 ,由已知
,由已知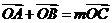 ,得
,得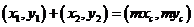
∴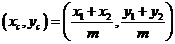 ,
,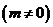
又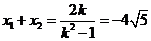 ,
,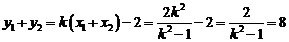
∴点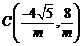 ,将点
,将点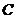 的坐标代入曲线
的坐标代入曲线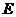 的方程,得
的方程,得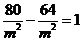
得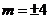 ,但当
,但当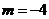 时,所得的点在双曲线的右支上,不合题意
时,所得的点在双曲线的右支上,不合题意
∴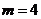 ,
,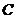 点的坐标为
点的坐标为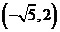 ,
,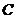 到
到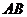 的距离为
的距离为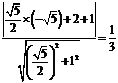
∴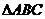 的面积
的面积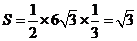 .
.
★★★高考要考什么
[考点透视]
近几年平面向量与解析几何交汇试题考查方向为
(1)考查学生对平面向量的概念、加减运算、坐标运算、数量积及学生对平面向量知识的简单运用,如向量共线、垂直、定比分点。
(2)考查学生把向量作为工具的运用能力,如求轨迹方程,圆锥曲线的定义,标准方程和几何性质,直线与圆锥曲线的位置关系。
[热点透析]
向量具有代数与几何形式的双重身份,故它是联系多项知识的媒介,成为中学数学知识的一个交汇点,数学高考重视能力立意,在知识网络的交汇点上设计试题,因此,解析几何与平面向量的融合交汇是今后高考命题改革的发展方向和创新的必然趋势。 要注意以平面向量作为工具,综合处理有关长度、角度、共线、平行、垂直、射影等问题以及圆锥曲线中的轨迹、范围、最值、定值、对称等典型问题。
★★★突破重难点
[范例1]设双曲线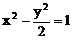 上两点A、B,AB中点M(1,2)
上两点A、B,AB中点M(1,2)
(1)求直线AB方程;
(2)如果线段AB的垂直平分线与双曲线交于C、D两点,那么A、B、C、D
是否共圆,为什么?
解析:(1)法一:显然AB斜率存在。 设AB:y-2=k(x-1)
由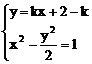 得(2-k2)x2-2k(2-k)x-k2+4k-6=0
得(2-k2)x2-2k(2-k)x-k2+4k-6=0
当△>0时,设A(x1,y1),B(x2,y2),则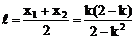
∴ k=1,满足△>0 ∴ 直线AB:y=x+1
法二:设A(x1,y1),B(x2,y2), 则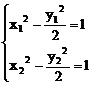
两式相减得(x1-x2)(x1+x2)=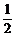 (y1-y2)(y1+y2)
(y1-y2)(y1+y2)
∵ x1≠x2
∴ 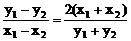 ∴
∴ 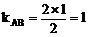
∴ AB:y=x+1 代入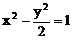 得△>0.
得△>0.
(2)设A、B、C、D共圆于⊙M¢,因AB为弦,故M¢在AB垂直平分线即CD上;又CD为弦,故圆心M¢为CD中点。因此只需证CD中点M满足|M¢A|=|M¢B|=|M¢C|=|M¢D|
由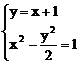 得A(-1,0),B(3,4). 又CD方程:y=-x+3
得A(-1,0),B(3,4). 又CD方程:y=-x+3
由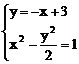 得x2+6x-11=0. 设C(x3,y3),D(x4,y4),CD中点M¢( x0,y0)
得x2+6x-11=0. 设C(x3,y3),D(x4,y4),CD中点M¢( x0,y0)
则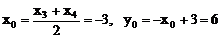 ∴ M¢(-3,6)
∴ M¢(-3,6)
∴ |M¢C|=|M¢D|=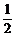 |CD|=
|CD|=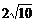
又|M¢A|=|M¢B|=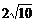 ∴ |M¢A|=|M¢B|=|M¢C|=|M¢D|
∴ |M¢A|=|M¢B|=|M¢C|=|M¢D|
∴ A、B、C、D在以CD中点,M¢(-3,6)为圆心,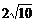 为半径的圆上
为半径的圆上
[点晴]第(1)小题中法一为韦达定理法,法二称为点差法,当涉及到弦的中点时,常用这两种途径处理。在利用点差法时,必须检验条件△>0是否成立;第(2)小题此类探索性命题通常肯定满足条件的结论存在,然后求出该结论,并检验是否满足所有条件,本题应着重分析圆的几何性质,以定圆心和定半径这两定为中心。充分分析平面图形的几何性质可以使解题思路更清晰,在复习中必须引起足够重视。
[文]在平面直角坐标系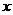 O
O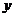 中,直线
中,直线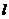 与抛物线y2=2x相交于A、B两点.
与抛物线y2=2x相交于A、B两点.
(1)求证:“如果直线l过点T(3,0),那么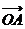
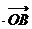 =3”是真命题;
=3”是真命题;
(2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由.
[解](1)设过点T(3,0)的直线l交抛物线y2=2x于点A(x1,y1)、B(x2,y2).
当直线l的钭率不存在时,直线l的方程为x=3,此时,直线l与抛物线相交于
点A(3,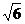 )、B(3,-
)、B(3,-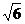 ).
∴
).
∴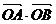 =3;
=3;
当直线l的钭率存在时,设直线l的方程为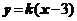 ,其中
,其中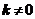 ,
,
由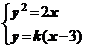 得
得 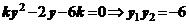
又 ∵ 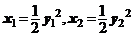 ,
,
∴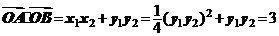 ,
,
综上所述,命题“如果直线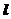 过点T(3,0),那么
过点T(3,0),那么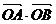 =3”是真命题;
=3”是真命题;
(2)逆命题是:设直线l交抛物线y2=2x于A、B两点,如果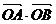 =3,那么该直线过点T(3,0).该命题是假命题.
=3,那么该直线过点T(3,0).该命题是假命题.
例如:取抛物线上的点A(2,2),B(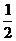 ,1),此时
,1),此时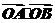 =3,直线AB的方程为:
=3,直线AB的方程为: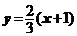 ,而T(3,0)不在直线AB上;
,而T(3,0)不在直线AB上;
说明:由抛物线y2=2x上的点A (x1,y1)、B (x2,y2)
满足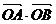 =3,可得y1y2=-6,或y1y2=2,如果y1y2=-6,可证得直线AB过点(3,0);如果y1y2=2,可证得直线AB过点(-1,0),而不过点(3,0).
=3,可得y1y2=-6,或y1y2=2,如果y1y2=-6,可证得直线AB过点(3,0);如果y1y2=2,可证得直线AB过点(-1,0),而不过点(3,0).
[范例2]已知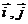 是x,y轴正方向的单位向量,设
是x,y轴正方向的单位向量,设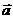 =
=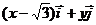 ,
,
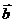 =
=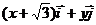 ,且满足
,且满足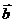 ·
·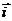 =|
=|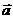 |.求点P(x,y)的轨迹.
|.求点P(x,y)的轨迹.
解:法一: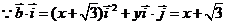 ,
,
∴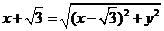 ,化简得
,化简得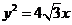 ,
,
故点P的轨迹是以(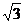 ,0)为焦点以
,0)为焦点以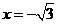 为准线的抛物线
为准线的抛物线
 法二:
法二: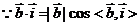
则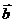
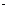
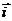 表示
表示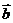 在
在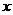 轴上的投影,
轴上的投影,
即点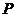 到
到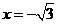 的距离,
的距离,
设F1 (-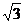 ,0),F2(
,0),F2(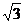 ,0),
,0),
所以点P到定点F2的距离与到定直线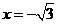 的距离相等,
的距离相等,
故点P的轨迹是以(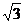 ,0)为焦点以
,0)为焦点以
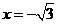 为准线的抛物线。
为准线的抛物线。
[点晴]将向量问题坐标化进而数量化(法一)和将向量问题几何化(法二)是两种常用转化方法,应熟练掌握。
[文]已知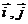 是x,y轴正方向的单位向量,设
是x,y轴正方向的单位向量,设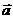 =
=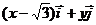 ,
, 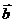 =
=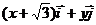 ,且满足|
,且满足|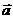 |+|
|+|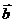 |=4.
|=4.
(1) 求点P(x,y)的轨迹C的方程.
(2)
如果过点Q(0,m)且方向向量为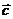 =(1,1) 的直线l与点P的轨迹交于A,B两点,当
=(1,1) 的直线l与点P的轨迹交于A,B两点,当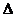 AOB的面积取到最大值时,求m的值。
AOB的面积取到最大值时,求m的值。
解:(1)
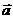 =
=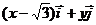 ,
,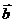 =
=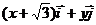 ,且|
,且|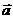 |+|
|+|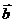 |=4.
|=4.
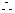 点P(x,y)到点(
点P(x,y)到点(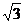 ,0),(-
,0),(-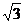 ,0)的距离这和为4,故点P的轨迹方程为
,0)的距离这和为4,故点P的轨迹方程为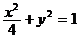
(2)设A(x1,y1),B(x2,y2)依题意直线AB的方程为y=x+m.代入椭圆方程,得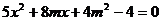 ,则
,则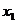 +
+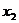 =-
=-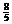 m,
m, 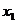 ·
·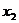 =
=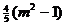
因此,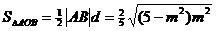
当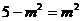 时,即m=
时,即m=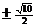 时,
时,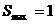
[范例3]已知点A(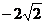 ,0),B(
,0),B(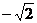 ,0)动点P满足
,0)动点P满足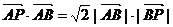
(1)若动点P的轨迹记作曲线C1,求曲线C1的方程.
(2)已知曲线C1交y轴正半轴于点Q,过点D(0,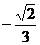 )作斜率为k的直线交曲线C1于M、N点,求证:无论k如何变化,以MN为直径的圆过点Q.
)作斜率为k的直线交曲线C1于M、N点,求证:无论k如何变化,以MN为直径的圆过点Q.
解:(1)设P(x,y),则有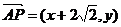
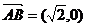
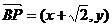
∵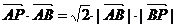 ∴
∴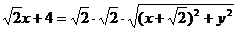
得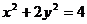
(2)由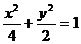 得Q (0,
得Q (0,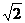 ) 设直线C的方程为y=kx-
) 设直线C的方程为y=kx-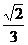
代入x2+2y2=4得 (1+2k2)
x2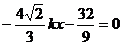
设M(x1,y1)
N(x2,y2) 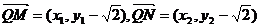
∵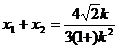
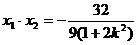
又∵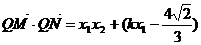
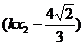 =
=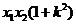
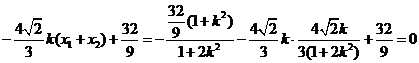
∴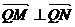 ∴点Q在以MN为直径的圆上.
∴点Q在以MN为直径的圆上.
 [点晴]直接法求轨迹是最常见的方法,要注意运用;向量是将几何问题代数化的有力工具。
[点晴]直接法求轨迹是最常见的方法,要注意运用;向量是将几何问题代数化的有力工具。
[文]如图,过抛物线x2=4y的对称轴上任一点
P(0,m)(m>0)作直线与抛物线交于A,B两点,点
Q是点P关于原点的对称点.设点P分有向线段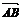 所
所
成的比为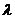 ,证明:
,证明:
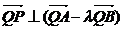 ;
;
解:依题意,可设直线AB的方程为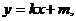
代入抛物线方程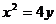 得
得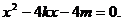 ①
①
设A、B两点的坐标分别是 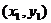 、
、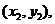
则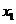 、x2是方程①的两根. 所以
、x2是方程①的两根. 所以 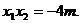
由点P(0,m)分有向线段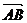 所成的比为
所成的比为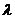 ,得
,得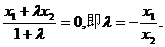
又点Q是点P关于原点的对称点,
故点Q的坐标是(0,-m),从而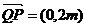 .
.
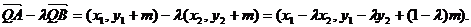
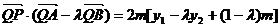
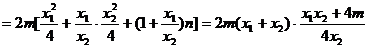
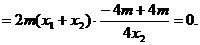
所以 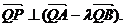
[范例4]已知A,B为抛物线x2=2py(p>0)上异于原点的两点,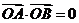 ,点C坐标为(0,2p)
,点C坐标为(0,2p)
(1)求证:A,B,C三点共线;
(2)若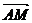 =
=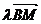 (
(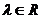 )且
)且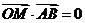 试求点M的轨迹方程。
试求点M的轨迹方程。
(1)证明:设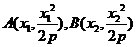 ,由
,由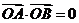 得
得
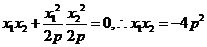 ,
,
又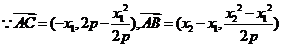
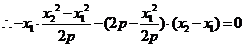 ,
,
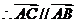 ,即A,B,C三点共线。
,即A,B,C三点共线。
(2)由(1)知直线AB过定点C,又由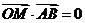 及
及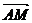 =
=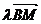 (
(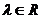 )知OM^AB,垂足为M,所以点M的轨迹为以OC为直径的圆,除去坐标原点。即点M的轨迹方程为x2+(y-p)2=p2(x¹0,y¹0)。
)知OM^AB,垂足为M,所以点M的轨迹为以OC为直径的圆,除去坐标原点。即点M的轨迹方程为x2+(y-p)2=p2(x¹0,y¹0)。
[点晴]两个向量的平行(共线)与垂直的充要条件在解析几何中有重要应用。在解题时尤其要注意几何位置Û向量表达式Û坐标表示之间的转化。
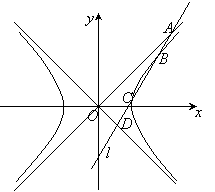
[文]已知双曲线M:x2-y2=1,直线l与双曲线M的实轴不垂直,且依次交直线y=x、双曲线M、直线y=-x于A、B、C、D 四点,O为坐标原点.
(1) 若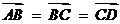 ,求△AOD的面积;
,求△AOD的面积;
(2) 若△BOC的面积等于△AOD面积的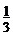 ,求证:
,求证: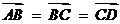 .
.
 解:(1)设
解:(1)设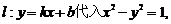
得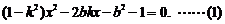
显然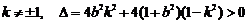 ,
,
即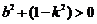 .
.
设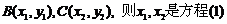 的两
的两
个根,有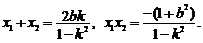
设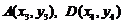
由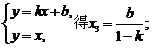 。
。
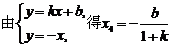
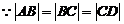 , 所以
, 所以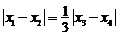 。
。
所以 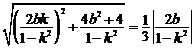 , 整理,得
, 整理,得 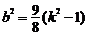 .
.
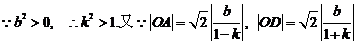 ,
, 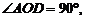
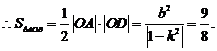
(2)设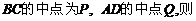
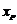
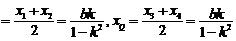 ,
,

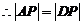 ,
, 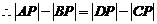 ,
, 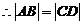 .
.
又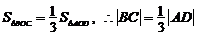 ,
, 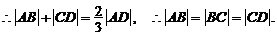
★★★自我提升
5.若曲线y2=|x|+1与直线y=kx+b没有公共点,则k、b分别应满足的条件是
.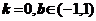
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com