
6.这是一个计算机程序的操作说明:
(1)初始值为x=1,y=1,z=0,n=0;
(2)n=n+1(将当前n+1的值赋予新的n)
(3)x = x+2(将当前的x=2的值赋予新的x)
(4)y =2 y (将当前2y的值赋予新的y)
(5)z = z + x y(将当前z+xy的值赋予新的z)
(6)如果z>7000,则执行语句(7),否则回语句(2)继续进行;
(7)打印n,z;
(8)程序终止.
由语句(7)打印出的数值为 n=8,z=7682 .
7.已知二次函数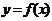 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为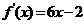 ,数列
,数列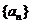 的前n项和为
的前n项和为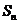 ,点
,点 均在函数
均在函数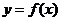 的图像上.
的图像上.
(Ⅰ) 求数列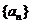 的通项公式;
的通项公式;
(Ⅱ) 设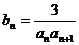 ,
,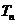 是数列
是数列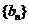 的前n项和,求使得
的前n项和,求使得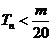 对所有
对所有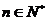 都成立的最小正整数m;
都成立的最小正整数m;
解析
(Ⅰ)设二次函数f (x)=ax2+bx (a≠0),则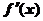 =2ax+b,又
=2ax+b,又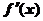 =6x-2,得a=3 , b=-2, 所以 f(x)=3x2-2x.
=6x-2,得a=3 , b=-2, 所以 f(x)=3x2-2x.
又因为点 均在函数
均在函数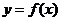 的图像上,所以
的图像上,所以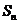 =3n2-2n.
=3n2-2n.
当n≥2时,an=Sn-Sn-1=(3n2-2n)-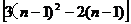 =6n-5.
=6n-5.
当n=1时,a1=S1=3×12-2=6×1-5,所以,an=6n-5 (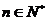 )
)
(Ⅱ)由(Ⅰ)得知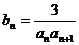 =
=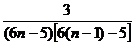 =
=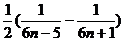 ,
,
故Tn=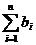 =
=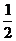
 =
=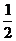 (1-
(1-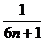 ).
).
因此,要使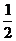 (1-
(1-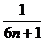 )<
)<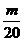 (
(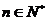 )恒成立的m,必须且仅须满足
)恒成立的m,必须且仅须满足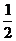 ≤
≤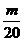 ,即m≥10,所以满足要求的最小正整数m为10.
,即m≥10,所以满足要求的最小正整数m为10.
[文]设等差数列{an}的首项a1及公差d都为整数,前n项和为Sn..
(Ⅰ)若a11=0,S14=98,求数列{an}的通项公式;
(Ⅱ)若a1≥6,a11>0,S14≤77,求所有可能的数列{an}的通项公式. 解析:(Ⅰ)由S14=98得2a1+13d=14, 又a11=a1+10d=0,故解得d=-2,a1=20.
因此,{an}的通项公式是an=22-2n,n=1,2,3…
(Ⅱ)由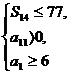 得
得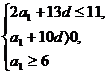 即
即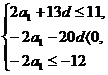
由①+②得-7d<11。即d>-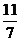 . 由①+③得13d≤-1,即d≤-
. 由①+③得13d≤-1,即d≤-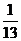 .
.
于是-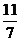 <d≤-
<d≤-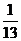 , 又d∈Z,故d=-1,将④代入①②得10<a1≤12.
, 又d∈Z,故d=-1,将④代入①②得10<a1≤12.
又a1∈Z, 故a1=11或a1=12.
所以,所有可能的数列{an}的通项公式是an=12-n和an=13-n,n=1,2,3,…
5.令a n为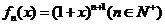 的展开式中含xn项的系数,则数列{a n}的前n项和为__________.
的展开式中含xn项的系数,则数列{a n}的前n项和为__________.
4.三个数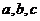 成等比数列,且
成等比数列,且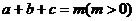 ,则
,则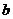 的取值范围是( D )
的取值范围是( D )
(A)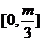 (B)
(B)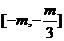 (C)
(C)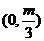 (D)
(D)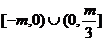
3.设{a n}为等差数列,a 1>0 ,a 6+ a 7>0, a6 a 7<0,则使其前n项和Sn>0成立的最大自然数n是( B )
(A)11 (B)12 (C)13 (D)14
2.(理)已知数列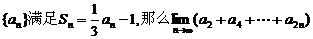 的值为( C )
的值为( C )
(A)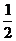 (B)
(B)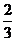 (C)1 (D)-2
(C)1 (D)-2
(文)直角三角形三边成等比数列,公比为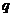 ,则
,则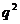 的值为( D )
的值为( D )
(A)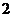 (B)
(B)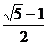 (C)
(C)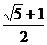 (D)
(D)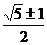
1.在等差数列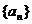 中,
中,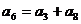 ,则
,则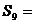 ( A )
( A )
(A)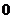 (B)
(B)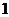 (C)
(C)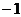 (D)-1或1
(D)-1或1
5. 若干个能唯一确定一个数列的量称为该数列的“基本量”.设{an}是公比为q的无穷等比数列,下列{an}的四组量中:①S1与S2; ②a2与S3; ③a1与an; ④q与an.
其中一定能成为该数列“基本量”的是第 ①④ 组.(写出所有符合要求的组号)
6.设数列{an}的首项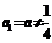 ,且
,且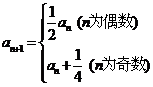 ,记
,记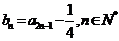 .
.
(I)求a2,a3;
(II)判断数列{bn}是否为等比数列,并证明你的结论;
(III)(理)求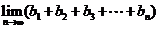 .
.
[专家解答]
(I)a2=a1+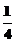 = a+
= a+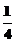 ,a3=
,a3=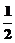 a2 =
a2 =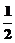 a+
a+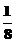 ;
;
(II)∵ a4 = a3+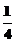 =
=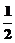 a+
a+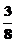 , ∴ a5=
, ∴ a5=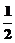 a4=
a4=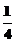 a+
a+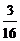 ,
,
所以b1=a1-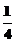 =a-
=a-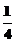 , b2=a3-
, b2=a3-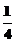 =
=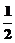 (a-
(a-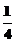 ), b3=a5-
), b3=a5-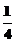 =
=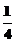 (a-
(a-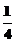 ),
),
猜想:{bn}是公比为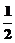 的等比数列.证明如下:
的等比数列.证明如下:
因为bn+1=a2n+1-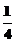 =
=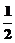 a2n-
a2n-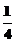 =
=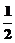 (a2n-1-
(a2n-1-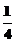 )=
)=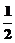 bn, (n∈N*)
bn, (n∈N*)
所以{bn}是首项为a-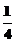 , 公比为
, 公比为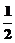 的等比数列·
的等比数列·
(III)(理)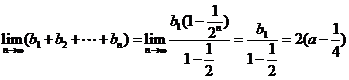 .
.
★★★高考要考什么
[考点透视]
本专题主要涉及等差(比)数列的定义、通项公式、前n项和及其性质,数列的极限、无穷等比数列的各项和.
[热点透析]
高考对本专题考查比较全面、深刻,每年都不遗漏.其中小题主要考查
 间相互关系,呈现“小、巧、活”的特点;大题中往往把等差(比)数列与函数、方程与不等式,解析几何
等知识结合,考查基础知识、思想方法的运用,对思维能力要求较高,注重试题的综合性,注意分类讨论.
间相互关系,呈现“小、巧、活”的特点;大题中往往把等差(比)数列与函数、方程与不等式,解析几何
等知识结合,考查基础知识、思想方法的运用,对思维能力要求较高,注重试题的综合性,注意分类讨论.
★★★突破重难点
[范例1]已知等差数列前三项为a,4,3a,前n项和为Sn,Sk = 2550.
(Ⅰ) 求a及k的值; (Ⅱ) 求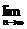 (
(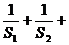 …
…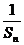 ).
).
解析(Ⅰ)设该等差数列为{an},则a1 = a,a2 = 4,a3 = 3a,Sk = 2550.
由已知得a+3a = 2×4, 解得a1 = a = 2,公差d = a2-a1= 2.
由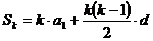 得
得 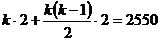 ,解得 k = 50.
,解得 k = 50.
∴ a = 2,k = 50.
(Ⅱ)由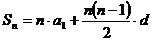 得Sn= n (n+1),
得Sn= n (n+1),
∴ 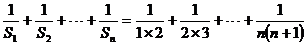
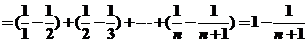 ,
,
∴ 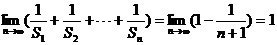 .
.
[点睛]错位相减法、裂项相消法等等是常用的数列求和方法.
[文]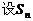 是等差数列
是等差数列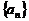 的前n项和,已知
的前n项和,已知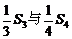 的等比中项为
的等比中项为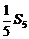 ,
,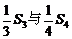 的等差中项为1,求数列
的等差中项为1,求数列 的通项.
的通项.
解析 由已知得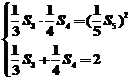 , 即
, 即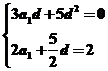 ,
,
解得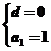 或
或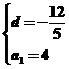
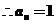 或
或 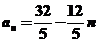
经验证
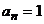 或
或 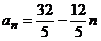 均满足题意,即为所求.
均满足题意,即为所求.
[点睛]若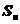 是等差数列
是等差数列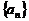 的前n项和,则数列
的前n项和,则数列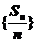 也是等差数列.本题是以此背景设计此题.
也是等差数列.本题是以此背景设计此题.
[范例2]已知正项数列{an},其前n项和Sn满足10Sn=an2+5an+6且a1, a3, a15成等比数列,求数列{an}的通项an .
解析 ∵10Sn=an2+5an+6, ① ∴10a1=a12+5a1+6,解之得a1=2或a1=3.
又10Sn-1=an-12+5an-1+6(n≥2), ②
由①-②得 10an=(an2-an-12)+6(an-an-1),即(an+an-1)(an-an-1-5)=0
∵an+an-1>0 , ∴an-an-1=5 (n≥2).
当a1=3时,a3=13,a15=73. a1, a3,a15不成等比数列∴a1≠3;
当a1=2时, a3=12, a15=72, 有 a32=a1a15 , ∴a1=2, ∴an=5n-3.
[点睛]求数列的通项公式是数列的基本问题,一般有三种类型:(1)已知数列是等差或等比数列,求通项,破解方法:公式法或待定系数法;(2)已知Sn,求通项,破解方法:利用Sn-Sn-1= an,但要注意分类讨论,本例的求解中检验必不可少,值得重视;(3)已知数列的递推公式,求通项,破解方法:猜想证明法或构造法。
[文]已知等比数列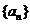 的前
的前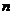 项和为
项和为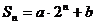 ,且
,且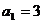 .
.
(1)求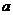 、
、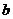 的值及数列
的值及数列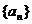 的通项公式;
的通项公式;
(2)设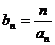 ,求数列
,求数列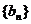 的前
的前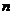 项和
项和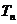 .
.
解析 (1)当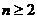 时,
时,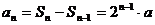 .
.
而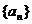 为等比数列,得
为等比数列,得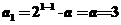 ,即
,即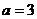 ,从而
,从而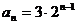 .
.
又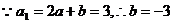 .
.
(2)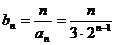 ,
, 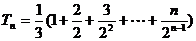
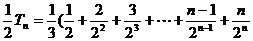
两式相减得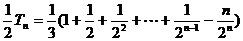 ,
,
因此,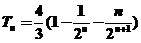 .
.
[范例3]下表给出一个“三角形数阵”:
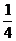
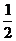 ,
,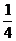
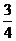 ,
,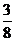 ,
,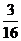
… … … …
已知每一列的数成等差数列;从第三行起,每一行的数成等比数列,每一行的公比都相等.记第i行第j列的数为aij ( i≥j, i, j∈N*).
(1) 求a83;
(2) 试写出a ij关于i, j的表达式;
(3) 记第n行的和为An,求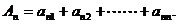
解析 (1)由题知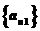 成等差数列,且
成等差数列,且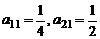 ,所以公差
,所以公差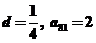 。
。
又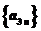 成等比数列,且
成等比数列,且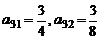 .又公比都相等,∴每行的公比是
.又公比都相等,∴每行的公比是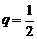 .
.
∴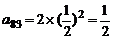 .
.
(2)由(1)知,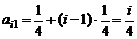 ,∴
,∴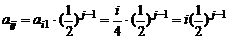 .
.
(3)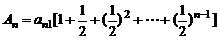
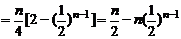 .
.
[点睛]在新颖背景--数表中运用数列知识.
[文]在等比数列{a n}中,前n项和为Sn,若Sm,Sm+2,Sm+1成等差数列,则am, am+2, am+1成等差数列
(1)写出这个命题的逆命题;(2)判断逆命题是否为真,并给出证明
解析(1)逆命题:在等比数列{an}中,前n项和为Sn,若am, am+2, am+1成等差数列,则 Sm,Sm+2,Sm+1成等差数列
(2)设{an}的首项为a1,公比为q. 由已知得2am+2= am + am+1
∴2a1qm+1=a1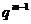 +a1qm ∵a1≠0 q≠0 ,∴2q2-q-1=0 , ∴q=1或q=-
+a1qm ∵a1≠0 q≠0 ,∴2q2-q-1=0 , ∴q=1或q=-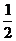

当q=1时,∵Sm=ma1, Sm+2= (m+2)a1,Sm+1= (m+1)a1,
∴Sm+Sm+1≠2 Sm+2, ∴Sm,Sm+2,Sm+1不成等差数列
当q=-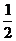 时,
时, 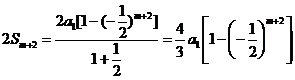 ,
,
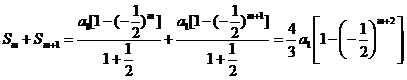
∴Sm+Sm+1=2 Sm+2
, ∴Sm,Sm+2,Sm+1成等差数列
综上得:当公比q=1时,逆命题为假;当公比q≠1时,逆命题为真
[点睛]逆命题中证明需分类讨论是本题的亮点和灵活之处.
[范例4]已知数列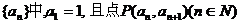 在直线x-y+1=0上.
在直线x-y+1=0上.
(1) 求数列{an}的通项公式;
(2)若函数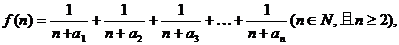
求函数f (n)的最小值;
(3)设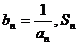 表示数列{bn}的前n项和. 试问:是否存在关于n 的整式g(n), 使得
表示数列{bn}的前n项和. 试问:是否存在关于n 的整式g(n), 使得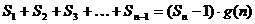 对于一切不小于2的自然数n恒成立?若存在,写出g(n)的解析式,并加以证明;若不存在,说明理由.
对于一切不小于2的自然数n恒成立?若存在,写出g(n)的解析式,并加以证明;若不存在,说明理由.
解析 (1)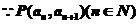 在直线x-y+1=0上
在直线x-y+1=0上 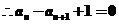
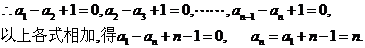
(2) 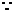
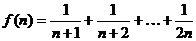 ,
,
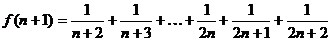 ,
,
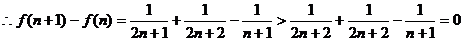 .
.
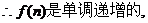

(3)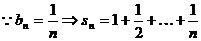 ,
,
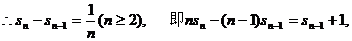
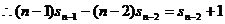 .
.
……………………………………
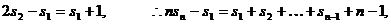
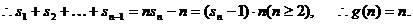
故存在关于n的整式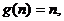 使等式对于一切不小2的自然数n恒成立.
使等式对于一切不小2的自然数n恒成立.
[点睛]点在直线上的充要条件是点的坐标满足直线的方程,即得递推式.第(3)小题的探索性设问也是本题的升华.
[变式]设数列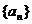 是等差数列,
是等差数列,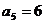 .
.
(Ⅰ)当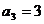 时,请在数列
时,请在数列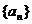 中找一项
中找一项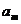 ,使得
,使得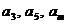 成等比数列;
成等比数列;
(Ⅱ)当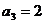 时,若
时,若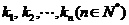 满足
满足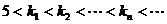 ,
,
使得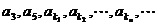 是等比数列,求数列
是等比数列,求数列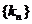 的通项公式.
的通项公式.
解析(Ⅰ)设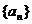 公差为
公差为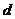 ,则由
,则由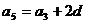 ,得
,得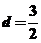
∵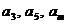 成等比数列,∴
成等比数列,∴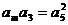 解得
解得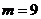 .故
.故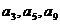 成等比数列.
成等比数列.
(Ⅱ)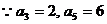 ,∴
,∴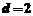 ,故
,故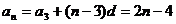 .
.
又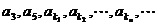 是等比数列,
是等比数列,
则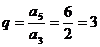 ,∴
,∴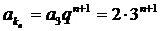 ,
,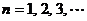
又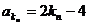 ,∴
,∴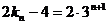 ,∴
,∴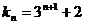
[点睛]等差数列中寻找等比子数列是数列的重要内容.
★★★自我提升
4.在等比数列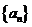 中,
中,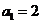 ,前
,前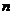 项和为
项和为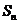 ,若数列
,若数列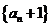 也是等比数列,则
也是等比数列,则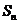 等于( C )
等于( C )
(A)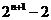 (B)
(B)
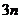 (C)
(C) 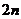 (D)
(D)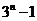
3.已知数列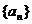 、
、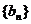 都是公差为1的等差数列,其首项分别为
都是公差为1的等差数列,其首项分别为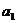 、
、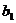 ,且
,且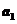
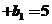 ,
,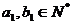 .设
.设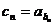 (
(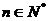 ),则数列
),则数列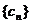 的前10项和等于( C )
的前10项和等于( C )
(A)55 (B)70 (C)85 (D)100
11.(理)A、B两队进行某项运动的比赛,以胜三次的一方为冠军,设在每次比赛中A胜的概率为p,B胜的概率为 ,又A得冠军的概率为P,冠军的概率为Q,决定冠军队的比赛次数为N.
(1)求使P-p为最大的p值;
(2)求使N的期望值为最大的p值及期望值。
(1)要决定冠军队,至少需要比赛三次,最多需要比赛5次。
解答:如果比赛3次A获冠军,A需连胜三次,其获冠军的概率为p3;
如果比赛4次A获冠军,前三次有一次B胜,其余三次A胜,A获冠军的概率为
如果比赛5次A获冠军,前四次有两次B胜,其余三次A胜,A获冠军的概率为
于是
将 代入整理得
令
即
当 时, 又
(2)随机变量N的概率分布为
|
N |
3 |
4 |
5 |
|
Q |
|
|
|
则
而
这时,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com