
2、若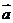 与
与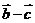 都是非零向量,则“
都是非零向量,则“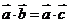 ”是“
”是“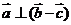 ”的( C )
”的( C )
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
1、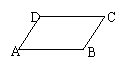 如图,在平行四边形ABCD中,下列结论中错误的是 ( C )
如图,在平行四边形ABCD中,下列结论中错误的是 ( C )
(A)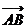 =
=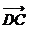 ;
(B)
;
(B)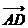 +
+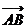 =
=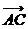 ;
;
(C)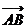 -
-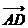 =
=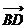 ; (D)
; (D)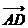 +
+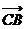 =
= .
.
8.在正三角形ABC的边AB、AC上分别取D、E两点,使沿线段DE折叠三角形时,顶点A正好落在边BC上,在这种情况下,若要使AD最小,求AD∶AB的值.
解析 按题意,设折叠后A点落在边BC上改称P点,显然A、P两点关于折线DE对称,又设∠BAP=θ,∴∠DPA=θ,∠BDP=2θ,再设AB=a,AD=x,
∴DP=x.在△ABC中,∠APB=180°-∠ABP-∠BAP=120°-θ,
由正弦定理知: .∴BP=
在△PBD中, ,
∵0°≤θ≤60°,∴60°≤60°+2θ≤180°,
∴当60°+2θ=90°,即θ=15°时,sin(60°+2θ)=1,
此时x取得最小值 a,即AD最小,
∴AD∶DB=2 -3.
[文]在 中, 分别为角 的对边,且满足
(1)求角 大小;
(2)若 ,当 取最小值时,判断 的形状.
解析(1) ,
,
. ,
, .
(2)由余弦定理 ,得 .
, .
所以 的最小值为 ,当且仅当 时取等号.此时 为正三角形.
5. 已知a+1,a+2,a+3是钝角三角形的三边,则a的取值范围是 . (0,2)
6.已知定义在R上的偶函数 在区间 上单调递增,若
的内角A满足 ,则A的取值范围是 ___
7.数列{a n}中,首项a1=2,前n项和为Sn,且 .
(1)判断数列{a n}是否为等比数列,并证明你的结论?
(2)若对每个正整数n,以a n,a n+1,a n+2为边长都能构成三角形,求t的取值范围。
解析 (1)略
(2)
[文]在 中, . . 的对边分别为 . . 。
(1) 若a,b,c 成等比数列,求f(B)=sinB+ cosB的值域。
(2) 若a,b,c 成等差数列,且A-C= ,求cosB的值。
解析 (1) ∵ ,
当且仅当 时取等号, ∵f(B)=sinB+ cosB=
∵ ∴ 的值域为
(2) ∵ ∴ sinA+sinC=2sinB ∵
∴ C= ∴sin( )+sin( )=2sinB
展开,化简,得 , ∵ , ∴
∴ cosB=
4.一个直角三角形三内角的正弦值成等比数列,其最小内角为( A )
(A)arccos (B)arcsin (C)arccos (D)arcsin
3.△ABC中,3sinA+4cosB=6,3cosA+4sinB=1,则∠C的大小是 ( A )
(A) (B) (C) 或 (D) 或
2.已知非零向量 与 满足 且 则 为( D )
(A)等边三角形 (B)直角三角形
(C)等腰非等边三角形 (D)三边均不相等的三角形
3.在△ABC中,已知A、B、C成等差数列,则 的值为__________ .
4.如果 的三个内角的余弦值分别等于 的三个内角的正弦值,则()
A. 和 都是锐角三角形
B. 和 都是钝角三角形
C. 是钝角三角形, 是锐角三角形
D. 是锐角三角形, 是钝角三角形
5.己知A、C是锐角△ABC的两个内角,且tanA, tanC是方程x2- px+1-p=0
(p≠0,且p∈R),的两个实根,则tan(A+C)=_______,tanA,tanC的取值范围分别是___ _
和__ ___,p的取值范围是__________ ;(0, );(0, );[ ,1)
6.在ΔABC中,已知 ,AC边上的中线BD= ,求sinA.
[专家解答] 设E为BC的中点,连接DE,则DE//AB,且 ,
设BE=x 在ΔBDE中可得 ,
,解得 , (舍去)
故BC=2,从而 ,
即 又 ,故 ,
★★★高考要考什么
[考点透视]
本专题主要考查正弦定理和余弦定理.
[热点透析]
三角形中的三角函数关系是历年高考的重点内容之一,本节主要帮助考生深刻理解正、余弦定理,掌握解斜三角形的方法和技巧 学生需要掌握的能力:
(1)运用方程观点结合恒等变形方法巧解三角形;
(2)熟练地进行边角和已知关系式的等价转化;
(3)能熟练运用三角形基础知识,正(余)弦定理及面积公式与三角函数公式配合,通过等价转化或构建方程解答三角形的综合问题,注意隐含条件的挖掘
★★★突破重难点
[范例1]在△ABC中,角A,B,C所对的边分别为a,b,c, b=acosC,且△ABC的最大边长为12,最小角的正弦值为 。
(1) 判断△ABC的形状;
(2) 求△ABC的面积。
解析(1) b=acosC, 由正弦定理,得sinB=sinAcosC, (#)
B= , sinB=sin(A+C),从而(#)式变为sin(A+C)= sinAcosC,
cosAsinC=0,又A,C cosA=0,A= , △ABC是直角三角形。
(2) △ABC的最大边长为12,由(1)知斜边 =12,又 △ABC最小角的正弦值为 , Rt△ABC的最短直角边为12 =4,另一条直角边为
S△ABC = =16
[点晴]此题主要考查三角函数变换及正弦定理的应用.用正弦定理化边为角,再以角为突破口,判断出△ABC的形状,最后由已知条件求出三条边,从而求面积.
[文]在△ABC中,若tanA︰tanB= ,试判断△ABC的形状.
解析 由同角三角函数关系及正弦定理可推得
∵A、B为三角形的内角,∴sinA≠0,sinB≠0.
∴2A=2B或2A=π-2B,∴A=B或A+B= .
所以△ABC为等腰三角形或直角三角形.
[点晴]三角形分类是按边或角进行的,所以判定三角形形状时一般要把条件转化为边之间关系或角之间关系式,从而得到诸如a2+b2=c2, a2+b2>c2(锐角三角形),a2+b2<c2(钝角三角形)或sin(A-B)=0,sinA=sinB,sinC=1或cosC=0等一些等式,进而判定其形状,但在选择转化为边或是角的关系上,要进行探索.
[范例2] 中,内角 . . 的对边分别为 . . ,已知 . . 成等比数列,且
(1)求 的值;
(2)若 ,求 的值
解析(1)由 得 ,由 得 ,
(2)由 得: ,因 ,所以: ,即:
由余弦定理 得
于是: 故
[点晴] 以三角形为载体,以三角变换为核心,结合正弦定理和余弦定理综合考查逻辑分析和计算推理能力是高考命题的一个重要方向,因此要特别关注三角函数在解斜三角形中的灵活应用.
[文]在△ABC中,a、b、c分别为角A、B、C的对边, .
(1)求角A的度数;
(2)若a= ,b+c=3,求b和c的值.
解析
[点睛]正弦定理和余弦定理在解斜三角形中应用比较广泛.
[范例3]已知△ABC的周长为6, 成等比数列,求
(1)△ABC的面积S的最大值;
(2) 的取值范围.
解析 设 依次为a,b,c,则a+b+c=6,b²=ac.
在△ABC中得 ,
故有 .又 从而 .
(1) ,即 .
(2)
.
.
[点睛] 三角与向量结合是高考命题的一个亮点.问题当中的字母比较多,这就需要我们采用消元的思想,想办法化多为少,消去一些中介的元素,保留适当的主变元.主变元是解答问题的基本元素,有效的控制和利用对调整解题思路是十分有益处的.
[变式]在△ABC中,角A、B、C的对边分别为a、b、c, △ABC的外接圆半径R= ,且满足 .
(1) 求角B和边b的大小;
(2) 求△ABC的面积的最大值。
解析 (1) 由 整理得sinBcosC+cosBsinC=2sinAcosB
∴sin(B+C)= 2sinAcosB ∴sinA=2sinAcosB ∴cosB= ∴B=
∵ b=2RsinB ∴b=3
(2)∵ =
∴当A= 时, 的最大值是 .
[点睛]三角函数的最值问题在三角形中的应用
[范例4]某观测站C在城A的南20˚西的方向上,由A城出发有一条公路,走向是南40˚东,在C处测得距C为31千米的公路上B处有一人正沿公路向A城走去,走了20千米后,到达D处,此时C、D间距离为21千米,问还需走多少千米到达A城?
解析 据题意得图02,其中BC=31千米,BD=20千米,CD=21千米,∠CAB=60˚.
设∠ACD = α ,∠CDB = β .在△CDB中,由余弦定理得:
,
.
.
在△ACD中得 .
所以还得走15千米到达A城.
[点晴] 运用解三角形的知识解决实际问题时,关键是把题设条件转化为三角形中的已知元素,然后解三角形求之.
[变式]已知半圆O的直径AB=2,P为AB延长线上一点,OP=2,Q为半圆上任意一点,以PQ为一边作等边三角形PQR(P、Q、R为顺时针排列),问点Q在什么位置时,四边形OPRQ面积最大,并求这个最大面积.
解析 设
面积 ,
而△POQ面积S2= ,
∴四边形OPRQ面积
.
[点睛]三角函数在实际问题中的应用问题.
★★★自我提升
1.在直角三角形中,两锐角为A和B,则sinA·sinB( B )
(A).有最大值 和最小值 (B).有最大值 但无最小值
(C).既无最大值也无最小值 (D).有最大值1但无最小值
8.已知函数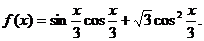
(Ⅰ)将f(x)写成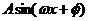 的形式,并求其图象对称中心的横坐标及对称轴方程
的形式,并求其图象对称中心的横坐标及对称轴方程
(Ⅱ)如果△ABC的三边a、b、c满足b2=ac,且边b所对的角为x,试求x的范围及此时函数f(x)的值域.
解析 (1)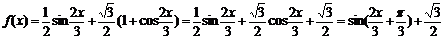
由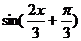 =0即
=0即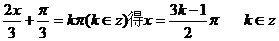
即对称中心的横坐标为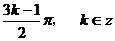
(Ⅱ)由已知b2=ac,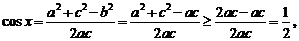
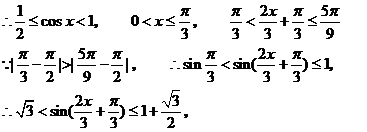
即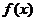 的值域为
的值域为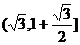 .
.
[文]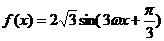 (ω>0)
(ω>0)
(1)若f (x +θ)是周期为2π的偶函数,求ω及θ值
(2)f (x)在(0,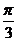 )上是增函数,求ω最大值。
)上是增函数,求ω最大值。
解析(1)因为f (x +θ)=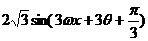
又f (x
+θ)是周期为2π的偶函数, 故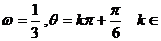 Z
Z
(2)因为f (x)在(0,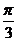 )上是增函数,故ω最大值为
)上是增函数,故ω最大值为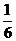
2.
为了得到函数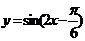 的图象,可以将函数
的图象,可以将函数 的图象( B )
的图象( B )
(A) 向右平移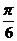 个单位长度 (B)向右平移
个单位长度 (B)向右平移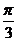 个单位长度
个单位长度
(C)向左平移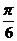 个单位长度 (D) 向左平移
个单位长度 (D) 向左平移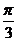 个单位长度
个单位长度
3.(理)函数y=sinx的定义域为[a,b],值域为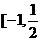 ],则b-a的最大值和最小值之和为( B )
],则b-a的最大值和最小值之和为( B )
(A)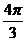 (B)2
(B)2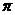 (C)
(C)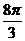 (D)
(D)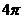
(文)函数f(x)=cos2x+sin(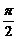 +x)是( D
)
+x)是( D
)
(A)非奇非偶函数 (B)仅有最小值的奇函数
(C)仅有最大值的偶函数 (D)既有最大值又有最小值的偶函数
4.给出四个命题,则其中正确命题的序号为 ( B )
① 存在一个△ABC,使得sinA+cosA=-1;
② △ABC中,A>B的充要条件为sinA>sinB;
③ 直线x=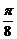 是函数y=sin(2x+
是函数y=sin(2x+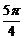 )图象的一条对称轴;
)图象的一条对称轴;
④ △ABC中,若sin2A=sin2B,则△ABC一定是等腰三角形.
(A)①② (B)②③ (C)③④ (D)①④
5.函数y = -2sin(4x+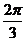 )的图象与x轴的交点中, 离原点最近的一点的坐标是___
)的图象与x轴的交点中, 离原点最近的一点的坐标是___
(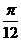 , 0)
, 0)
6.如果图象x2+y2≤k2至少覆盖函数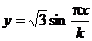 的一个最大值点和一个最小值点,则正整数k 的最小值为
2.
的一个最大值点和一个最小值点,则正整数k 的最小值为
2.
7.已知定义在区间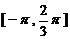 上的函数
上的函数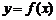 的图象关于直线
的图象关于直线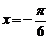 对称,当
对称,当
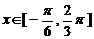 时,函数
时,函数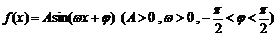 ,其图象如图.
,其图象如图.
(1)求函数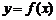 在
在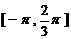 的表达式;
的表达式;
(2)求方程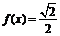 的解.
的解.
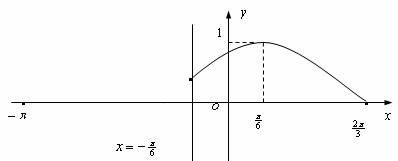
解析 (1)当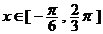 时,
时,
函数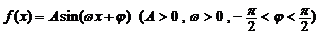 ,观察图象易得:
,观察图象易得:
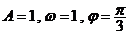 ,即函数
,即函数 ,由函数
,由函数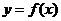 的图象关于直线
的图象关于直线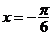 对称得,
对称得,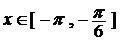 时,函数
时,函数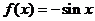 .
.
∴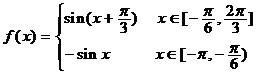 .
.
(2)当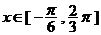 时,
时,
由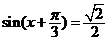 得,
得,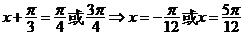 ;
;
当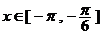 时,由
时,由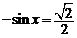 得,
得,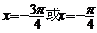 .
.
∴方程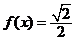 的解集为
的解集为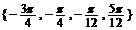
[文]已知函数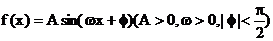 的图象在
的图象在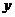 轴上的截距为1,它在
轴上的截距为1,它在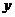 轴右侧的第一个最大值点和最小值点分别为
轴右侧的第一个最大值点和最小值点分别为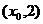 和
和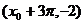 .
.
(1)试求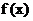 的解析式;
的解析式;
(2)将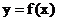 图象上所有点的横坐标缩短到原来的
图象上所有点的横坐标缩短到原来的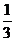 (纵坐标不变),然后再将新的图象向
(纵坐标不变),然后再将新的图象向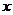 轴正方向平移
轴正方向平移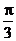 个单位,得到函数
个单位,得到函数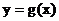 的图象.写出函数
的图象.写出函数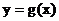 的解析式.
的解析式.
解析 (1)由题意可得: 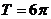 ,
, 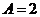 ,
,  ,
,
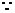 函数图像过(0,1),
函数图像过(0,1), 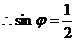 ,
, 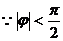 ,
,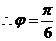 ,
,
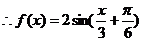 ;
;
(2)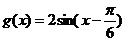
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com