6．　 在棱长为2的正方体中，O是底面ABCD的中心，E、F分别是、AD的中点，那么异面直线OE和所成的角的余弦值等于　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　　　　　　　　 )

　　　 A．　 　　　　　　 B．　　　 　　　　　　 C．　 　　　　　　　 D．

5．棱长都为2的直平行六面体ABCD-A₁B₁C₁D₁中，∠BAD=60°，则对角线A₁C与侧面DCC₁D₁所成角的正弦值为　　　 　　　　　　　　　　　　　　　　　　　 (　　　　　　　　　　　　　　 )

　　　 A．　　　　　　　　　 B．　　　　　　 C． 　　　　　　　　 D．

4．　 设E，F是正方体AC₁的棱AB和D₁C₁的中点，在正方体的12条面对角线中，与截面A₁ECF成60°角的对角线的数目是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　　　　　　　　　　　　　 )

A．0 　　　　　　　　　　　　　　 B．2 　　　　　　　　 C．4　　 　　　　　　　 D．6

3．正方体ABCD-A₁B₁C₁D₁中，E、F分别是AA₁与CC₁的中点，则直线ED与D₁F所成角的大小是　　　　　　　　　　　 (　　 )

A．　　　　　　　　　　　　　　 B。　　　　　　　　　　　 C。　　　　　　　　　　　 D。

2．在正三棱柱ABC-A₁B₁C₁中，若AB=BB₁,则AB₁与C₁B所成的角的大小为　　　　　　　　　

A.60º B. 90º C.105º D. 75º

1．在正三棱柱ABC-A₁B₁C₁中，若AB=2，A A₁=1，则点A到平面A₁BC的距离为(　　 )

　　　 A．　　　　　　　　　 B．　　　　　　　　　 C．　　　　　　　　 D．

5．设平面α的一个法向量为，点P是平面α外一点，且P_o∈α，则点P到平面α的距离是d＝.

第2课时　 空间向量的坐标运算

设a＝，b＝

(1) a±b＝　　　　　　　　

(2) a＝　　　　　　　　 ．

(3) a·b＝　　　　　 ．

(4) a∥b　　　　　　 ；ab　　　　 ．

(5) 设

则＝　　　　　　 ，　　　　　　　 ．

AB的中点M的坐标为　　　　　　　 　．

例1. 若＝(1,5,－1)，＝(－2,3,5)

(1)若(k+)∥(－3)，求实数k的值；

(2)若(k+)⊥(－3)，求实数k的值；

(3)若取得最小值，求实数k的值．

解：(1)；

(2)；　　 (3)

变式训练1. 已知为原点，向量∥，求．

解：设，

∵∥，∴，，

∴，即

解此方程组，得。

　　　 ∴，。

例2. 如图，直三棱柱，底面中，CA＝CB＝1，，棱，M、N分别A₁B₁、A₁A是的中点．

(1) 求BM的长；　

(2) 求的值；　

(3) 求证：．

解：以C为原点建立空间直角坐标系.

(1) 依题意得B(0，1，0)，M(1，0，1)．.

(2) 依题意得A₁(1，0，2)，B(0，1，0)，C(0，0，0)，B₁(0，1，2).

.

(3) 证明：依题意得C₁(0，0，2)，N.

变式训练2. 在四棱锥P－ABCD中， 底面ABCD为矩形，侧棱PA⊥底面ABCD，AB＝，BC＝1，PA＝2，E为PD的中点．

(1) 在侧面PAB内找一点N，使NE⊥面PAC，并求出N点到AB和AP的距离；

(2) 求(1) 中的点N到平面PAC的距离．

解：(1) 建立空间直角坐标系A－BDP，则A、B、C、D、P、E的坐标分别是A(0, 0, 0)、B(, 0, 0)、C(, 1, 0)、D(0, 1, 0)、P(0, 0, 2)、E(0, , 1)，依题设N(x, 0, z)，则＝(－x, , 1－z)，由于NE⊥平面PAC，

∴

即

，即点N的坐标为(, 0, 1)，

从而N到AB、AP的距离分别为1，.

(2) 设N到平面PAC的距离为d，则d＝

＝.

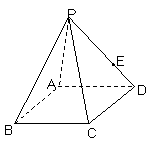例3. 如图，在底面是棱形的四棱锥中，，点E在上，且:＝2:1．

(1) 证明 平面；

(2) 求以AC为棱，与为面的二面角的大小；

(3) 在棱PC上是否存在一点F，使∥平面？证明你的结论．

解：(1)证明略；

(2)易解得；

(3)解　 以A为坐标原点，直线分别为y轴、z轴，过A点垂直于平面PAD的直线为x轴，建立空间直角坐标系(如图)．由题设条件，相关各点的坐标为

所以，，

，设点F是棱上的点，，其中，则．令得

解得，即时，．亦即，F是PC的中点时，共面，又平面，所以当F是PC的中点时，∥平面．

例4. 如图，多面体是由底面为ABCD的长方体被截面AEFG所截而得，其中AB＝4，BC＝1，BE＝3，CF＝4.

(1) 求和点G的坐标；

(2) 求GE与平面ABCD所成的角；

(3) 求点C到截面AEFG的距离．

解：(1) 由图可知：A(1，0，0)，B(1，4，0)，

E(1，4，3)，F(0，4，4)　 ∴

又∵，设G(0，0，z)，则(－1，0，z)

＝(－1，0，1)　 ∴z＝1　 ∴G(0，0，1)

(2)平面ABCD的法向量

，设GE与平面ABCD成角为，则

∴

(3)设⊥面AEFG，＝(x₀，y₀，z₀)

∵⊥，⊥，而＝(－1，0，1)，＝(0，4，3)

∴

取z₀＝4，则＝(4，－3，4)

∵

即点C到截面AEFG的距离为．

变式训练4. 如图四棱锥P-ABCD中，底面ABCD是平行四边形，PG⊥平面ABCD，垂足为G，G在AD上，且PG＝4，，BG⊥GC，GB＝GC＝2，E是BC的中点．

　　　 (1)求异面直线GE与PC所成的角的余弦值；

　　　 (2)求点D到平面PBG的距离；

　　　 (3)若F点是棱PC上一点，且DF⊥GC，求的值．

解：(1)以G点为原点，为x轴、y轴、

z轴建立空间直角坐标系，则B(2，0，0)，C(0，2，0)，

P(0，0，4)，故E(1，1，0)，＝(1，1，0)， ＝(0，2，4)。，

∴GE与PC所成的余弦值为．

　(2)平面PBG的单位法向量n＝(0，±1，0) .

∵，

∴点D到平面PBG的距离为n |＝.

　(3)设F(0，y，z)，则。

∵，∴，

即，

∴ , 又，即(0，，z－4)＝λ(0，2，－4)，　 ∴z=1，

对于以下几类立体几何问题：(1) 共线与共面问题；(2) 平行与垂直问题；(3) 夹角问题；(4) 距离问题；(5) 探索性问题．

运用向量来解决它们有时会体现出一定的优势．用空间向量解题的关键步骤是把所求向量用某个合适的基底表示，本节主要是用单位正交基底表示，就是适当地建立起空间直角坐标系，把向量用坐标表示，然后进行向量与向量的坐标运算，最后通过向量在数量上的关系反映出向量的空间位置关系，从而使问题得到解决．在寻求向量间的数量关系时，一个基本的思路是列方程，解方程．

空间向量章节测试题

4．异面直线间的距离的向量求法：已知异面直线l₁、l₂，AB为其公垂线段，C、D分别为l₁、l₂上的任意一点，为与共线的向量，则｜｜＝.

3．利用向量求夹角(线线夹角、线面夹角、面面夹角)有时也很方便．其一般方法是将所求的角转化为求两个向量的夹角，而求两个向量的夹角则可以利用公式cosθ＝．　

2．运用向量求解距离问题，其一般方法是找出代表相应距离的线段所对向量，然后计算这个向量对应的模．而计算过程中只要运用好加法法则，就总能利用一个一个的向量三角形，将所求向量用有模和夹角的已知向量表示出来，从而求得结果．