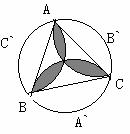
9．如图①、②、③中，点E、D分别是正△ABC、正四边形ABCM、正五

边形ABCMN中以C点为顶点的相邻两边上的点，且BE = CD，DB交AE于P点。

⑴求图①中，∠APD的度数；

⑵图②中，∠APD的度数为___________，图③中，∠APD的度数为___________；

⑶根据前面探索，你能否将本题推广到一般的正n 边形情况．若能，写出推广问题和结论；若不能，请说明理由。

B　 组

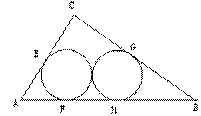
8．如图，ΔABC的∠C＝Rt∠，BC＝4，AC＝3，两个外切的等圆⊙O₁，⊙O₂各与AB，AC，BC相切于F，H，E，G，求两圆的半径。

7．如图，半径为2的正三角形ABC的中心为O，过O与两个顶点画弧，求这三条弧所围成的阴影部分的面积。

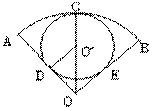
6．如图，已知扇形OACB中，∠AOB＝120°，弧AB长为L＝4π，⊙O′和弧AB、OA、OB分别相切于点C、D、E，求⊙O的周长。

5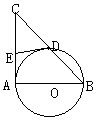．如图⊿ABC中∠A＝90°，以AB为直径的⊙O交BC于D，E为AC边中点，求证：DE是⊙O的切线。

4．如图，ABCD是⊙O的内接四边形，DP∥AC，交BA的延长线于P，求证：AD·DC＝PA·BC。

3．已知：如图20，在△ABC中，∠BAC=120°，AB=AC，BC=4，以A为圆心，2为半径作⊙A，试问：直线BC与⊙A的关系如何？并证明你的结论。

2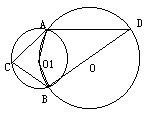．如图，⊙O₁的圆心在⊙O的圆周上，⊙O和⊙O₁交于A，B，AC切⊙O于A，连结CB，BD是⊙O的直径，∠D＝40°求：∠A O₁B、∠ACB和∠CAD的度数。

1．如图，P是⊙O外一点，PAB、PCD分别与⊙O相交于A、B、C、D。

(1)PO平分∠BPD； (2)AB=CD；(3)OE⊥CD，OF⊥AB；(4)OE=OF。

从中选出两个作为条件，另两个作为结论组成一个真命题，并加以证明。

10．如图7，在矩形ABCD中，已知AB=8 cm，将矩形绕点A旋转90°，到达A′B′C′D′的位置，则在转过程 中，边CD扫过的(阴影部分)面积S=_________。

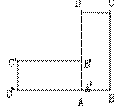
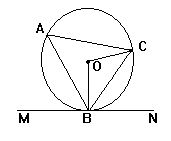
　　 图6　　　　　　　　　　　　　 图7