6．已知一次函数的图象与直线y=-x+1平行，且过点(8，2)，那么此一次函数的解析式为(　 )。

A．y=-x-2　　　 B．y=-x-6　　　 C．y=-x+10　　 D．y=-x-1

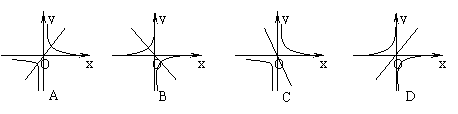
5．如图,在同一直角坐标系中，函数y=3x与y=图象大致是(　 )。

4．若二次函数y=x²－2x+c图象的顶点在x轴上，则c等于(　 )。

A.－1　　　　 B.1　　　　 C.　　　　　 　　 　　 D.2

3．如果反比例函数在其象限内，y随x的增大而减小，那么它的图象分布在(　 )。

A.第一、二象限　　　　　 B. 第一、三象限　

C. 第二、三象限　　　　　 D. 第二、四象限

2．若 ab＞0，bc<0，则直线y=－x－不通过(　 )。

A．第一象限　　 B第二象限　　 C．第三象限　　 D.第四象限

1．已知反比例函数 y= 的图象在第二、四象限，则a的取值范围是(　 )。

A.a≤2　　　 B.a ≥2　　　 C.a＜2　　　 D.a＞2

5.抛物线与x轴交点情况：

对于抛物线

①当时，抛物线与x轴有两个交点，反之也成立。

②当时，抛物线与x轴有一个交点，反之也成立，此交点即为顶点。

③当时，抛物线与x轴无交点，反之也成立。

A　　 组

4.求抛物线的顶点、对称轴和最值的方法

①配方法：将解析式y=ax²+bx+c化为y=a(x－h)²+k的形式，顶点坐标为(h，k)，对称轴为直线x=h，若a＞0，y有最小值，当x＝h时，y_最小值=k；若a＜0，y有最大值，当x＝h时，y_最大值=k。

②公式法：直接利用顶点坐标公式(　　　　　　　　　 )，求其顶点；对称轴是直线　　　　

　　　　　 ，若　　　　　　　　　　　　　　　　　　　　　　　　　　　 若，

y有最大值，当。

3.二次函数的性质

函数	二次函数y=ax2+bx+c (a、b、c为常数，a≠0)	y=a(x－h)2+k(a、h、k为常数，a≠0)
	a＞0	a＜0	a＞0	a＜0
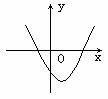
图象
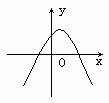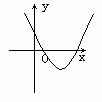	(1)抛物线开口向上，并向上无限延伸	(1)抛物线开口向下，并向下无限延伸	(1)抛物线开口向上，并向上无限延伸	(1)抛物线开口向下，并向下无限延伸
性	(2)对称轴是x＝，顶点是()	(2)对称轴是x＝，顶点是()	(2)对称轴是x＝h，顶点是(h，k)	(2)对称轴是x＝h，顶点是(h，k)
质	(3)当时，y随x的增大而减小；当时，y随x的增大而增大	(3)当时，y随x的增大而增大；当时，y随x的增大而减小	(3)当时，y随x的增大而减小；当x＞h时，y随x的增大而增大。	(3)当x＜h时，y随x的增大而增大；当x＞h时，y随x的增大而减小
	(4)抛物线有最低点，当时，y有最小值，	(4)抛物线有最高点，当时，y有最大值，	(4)抛物线有最低点，当x＝h时，y有最小值	(4)抛物线有最高点，当x＝h时，y有最大值

2.二次函数y=ax²+bx+c的图象

①二次函数y=ax²+bx+c的图象是对称轴平行于(包括重合)y轴的抛物线，几个不同的二次函数，如果a相同，那么抛物线的开口方向，开口大小(即形状)完全相同，只是位置不同。

②任意抛物线y=a(x－h)²+k可以由抛物线y=ax²经过适当的平移得到，移动规律可简记为：[左加右减，上加下减]，具体平移方法如下表所示。

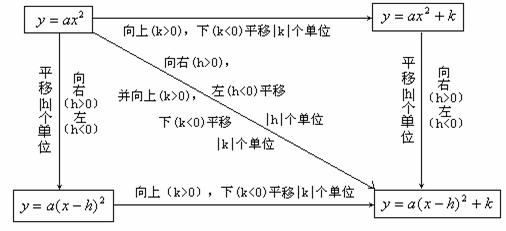
③在画y=ax²+bx+c的图象时，可以先配方成y=a(x－h)²+k的形式，然后将y=ax²的图象上(下)左(右)平移得到所求图象，即平移法；也可用描点法：也是将y=ax²+bx+c配成y=a(x－h)²+k的形式，这样可以确定开口方向，对称轴及顶点坐标。然后取图象与y轴的交点(0，c)，及此点关于对称轴对称的点(2h，c)；如果图象与x轴有两个交点，就直接取这两个点(x₁，0)，(x₂，0)就行了；如果图象与x轴只有一个交点或无交点，那应该在对称轴两侧取对称点，(这两点不是与y轴交点及其对称点)，一般画图象找5个点。