
22.根据函数的单调性,求参数的范围与恒成立问题。
()★★★已知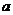 为实数,
为实数,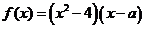 。
。
(1)求导数 ;(2)若
;(2)若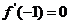 ,求
,求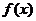 在
在 上的值域;(3)若
上的值域;(3)若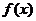 在
在 和
和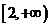 上都是递增函数,求
上都是递增函数,求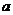 的取值范围
的取值范围
()★★★★(本题满分12分)已知函数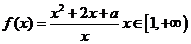 ,(1)当
,(1)当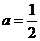 时,求函数
时,求函数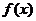 的最小值;(2)若对任意的
的最小值;(2)若对任意的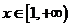 ,
,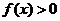 恒成立,试求实数
恒成立,试求实数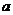 的取值范围。
的取值范围。
()(2006年江西卷)已知函数f(x)=x3+ax2+bx+c在x=-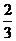 与x=1时都取得极值
与x=1时都取得极值
(1) 求a、b的值与函数f(x)的单调区间
(2) 若对xÎ(-1,2),不等式f(x)<c2恒成立,求c的取值范围。
⒘椭圆的几何性质:
()求椭圆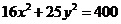 的长轴和短轴的长、离心率、焦点和顶点坐标及准线方程。
的长轴和短轴的长、离心率、焦点和顶点坐标及准线方程。
⒙根据两命题间的关系,求参数的取值范围:
已知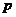 :
: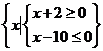 ;
;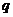 :
: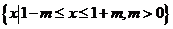 ,若
,若 是
是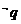 的必要不充分条件,求实数
的必要不充分条件,求实数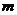 的取值范围。
的取值范围。
⒚抛物线的焦半径公式,及双曲线的渐近线求双曲线的方程:
⒛求函数在某点处的切线问题:
()★★若曲线 的切线垂直于直线
的切线垂直于直线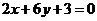 ,试求这条切线的方程。
,试求这条切线的方程。
()★★★★已知曲线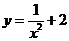 上有点
上有点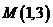 ,求:
,求:
(1)曲线在点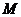 处的切线的斜率;(2)点
处的切线的斜率;(2)点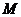 处的切线方程。
处的切线方程。
21.由椭圆的几何性质求椭圆的方程及弦长问题:
()已知长轴为12,短轴长为6,焦点在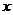 轴上的椭圆,过它对的左焦点
轴上的椭圆,过它对的左焦点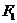 作倾斜解为
作倾斜解为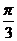 的直线交椭圆于
的直线交椭圆于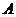 ,
, 两点,求弦
两点,求弦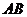 的长.
的长.
⒒全称(或特称)命题的否定:
()★★命题“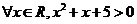 ”的否定是
。
”的否定是
。
()★★写出命题“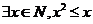 “的否定是
。
“的否定是
。
⒓已知抛物线的焦点求抛物线方程:
() ★顶点在原点,焦点是 的抛物线方程是
的抛物线方程是
()★★顶点在原点,焦点在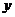 轴上,且过点
轴上,且过点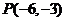 的抛物线的方程是
的抛物线的方程是
()★★经过点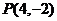 的抛物线的标准方程是
的抛物线的标准方程是
⒔求函数在给定区间上的最值:
()★★求函数 ,
,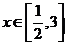 的最大值和最小值。
的最大值和最小值。
⒕求椭圆内以某定点为中点的弦所在的直线方程:
()已知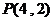 是直线
是直线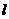 被椭圆
被椭圆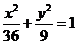 所截得的线段的中点,则直线
所截得的线段的中点,则直线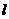 的方程
.
的方程
.
⒖利用导数求单调区间:
()★★函数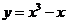 的单调减区间是 。
的单调减区间是 。
()★★★求函数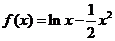 的单调增区间是
。
的单调增区间是
。
⒗关于椭圆的性质的综合问题:
()(2009重庆卷文)已知椭圆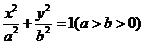 的左、右焦点分别为
的左、右焦点分别为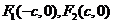 ,若椭圆上存在一点
,若椭圆上存在一点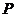 使
使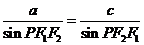 ,则该椭圆的离心率的取值范围为
.
,则该椭圆的离心率的取值范围为
.
()(2009江西卷理)过椭圆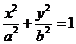 (
(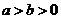 )的左焦点
)的左焦点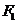 作
作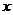 轴的垂线交椭圆于点
轴的垂线交椭圆于点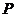 ,
,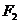 为右焦点,若
为右焦点,若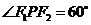 ,则椭圆的离心率为
,则椭圆的离心率为
⒈考查复合命题的真假判断:
(1)★如果命题“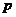 或
或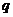 ”是真命题,“非
”是真命题,“非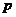 ”是假命题,那么( )
”是假命题,那么( )
A.命题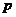 一定是假命题B.命题
一定是假命题B.命题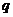 一定是假命题C.命题
一定是假命题C.命题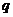 一定是真命题D.命题
一定是真命题D.命题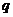 是真命题或假命题
是真命题或假命题
(2)★若命题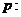
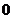 是偶数,命题
是偶数,命题
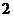 是
是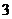 的约数,则下列命题中为真的是(
)
的约数,则下列命题中为真的是(
)
A.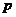 且
且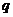 B.
B.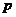 或
或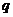 C.非
C.非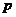 D.非
D.非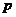 且非
且非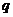
(3)★★设语句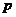 :
: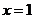 ,
,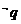 :
: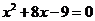 ,则下列选项中为真命题的是(
)
,则下列选项中为真命题的是(
)
A.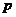 且
且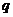 B.
B.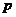 或
或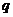 C.若
C.若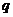 则
则 D.若
D.若 则
则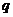
(4) ★★★命题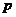 :
: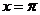 是
是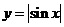 的一条对称轴,
的一条对称轴,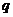 :
: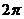 是
是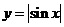 的最小正周期,有下列命题:①
的最小正周期,有下列命题:①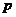 或
或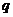 ;②
;②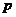 且
且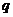 ;③非
;③非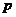 ;④非
;④非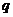 。其中真命的有( )
。其中真命的有( )
A.0个B.1个C.2个D.3个
⒉考查椭圆的第一定义:
(5) ★★椭圆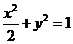 上的一点
上的一点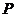 到焦点
到焦点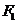 的距离等于
的距离等于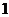 ,则点
,则点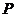 到另一个焦点
到另一个焦点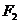 的距离是( )
的距离是( )
A.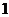 B.
B.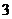 C.
C. D.
D.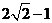
⒊四种命题及其真假的判断
(6)★★命题:“已知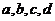 是实数,若
是实数,若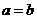 ,
,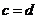 ,则
,则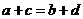 ”,对其原命题、逆命题、否命题呼逆否命题而言,真命题有( )
”,对其原命题、逆命题、否命题呼逆否命题而言,真命题有( )
A.0个B.2个C.3个D.4个
⒋有曲线的方程的类型讨论参数k的取值范围:
(7)★若方程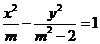 表示焦点在
表示焦点在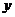 轴上的椭圆,那么实数
轴上的椭圆,那么实数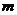 的取值范围是( )
的取值范围是( )
A.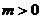 B.
B.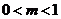 C.
C.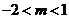 D.
D.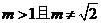
(8)★★若方程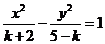 表示双曲线,则
表示双曲线,则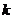 的取值范围是( )
的取值范围是( )
A.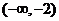 B.
B.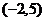 C.
C.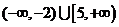 D.
D.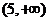
(9)★★★已知方程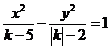 的图形是双曲线,则
的图形是双曲线,则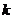 的取值范围是( )
的取值范围是( )
A.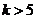 B.
B.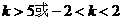 C.
C.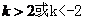 D.
D.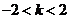
⒌求导函数的函数值:
(10)★★函数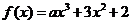 ,若
,若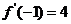 ,则
,则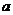 的值等于( )
的值等于( )
A.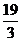 B.
B.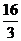 C.
C.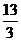 D.
D.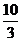
(11)★★★已知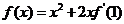 ,则
,则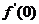 等于( )
等于( )
A.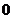 B.
B.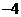 C.
C.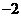 D.
D.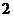
⒍已知双曲线的渐近线,求离心率e的值:
(12) ★★★设双曲线的焦点在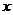 轴上,两条渐近线为
轴上,两条渐近线为 ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A.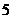 B.
B.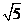 C.
C.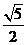 D.
D.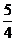
⒎由双曲线的定义求最短的焦半径:
()已知双曲线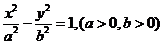 的左,右焦点分别为
的左,右焦点分别为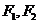 ,点P在双曲线的右支上,且
,点P在双曲线的右支上,且 ,则此双曲线的离心率e的最大值为:(
)
,则此双曲线的离心率e的最大值为:(
)
A 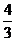 B
B 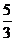 C
C 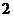 D
D 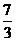
⒏已知曲线在某点处的切线方程,求切点坐标:
()★★如果曲线 的某一切线与直线
的某一切线与直线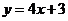 平行,求切点坐标。
平行,求切点坐标。
()★★★若直线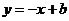 为函数
为函数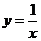 图象的切线,求
图象的切线,求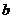 及切点坐标。
及切点坐标。
⒐抛物线的焦点与椭圆的离心率:
()双曲线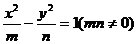 离心率为2,有一个焦点与抛物线
离心率为2,有一个焦点与抛物线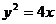 的焦点重合,则mn的值为( )
的焦点重合,则mn的值为( )
A.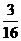 B.
B.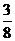 C.
C.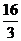 D.
D.
()设椭圆 (
(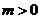 ,
,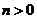 )的右焦点与抛物线
)的右焦点与抛物线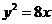 的焦点相同,离心率为
的焦点相同,离心率为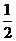 ,则此椭圆的方程为
,则此椭圆的方程为
(A)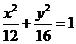 (B)
(B)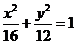 (C)
(C) (D)
(D)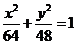
⒑原函数与导函数的图像关系问题(分类讨论思想):
 ()(2005江西卷理第7题)已知函数
()(2005江西卷理第7题)已知函数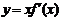 的图象如右图所示(其中
的图象如右图所示(其中 是函数
是函数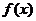 的导函数),下面四个图象中
的导函数),下面四个图象中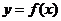 的图象大致是( )
的图象大致是( )
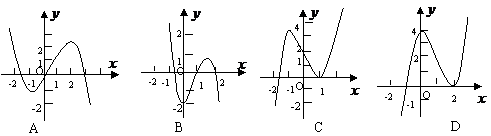

()(2004年浙江卷11)设f '(x)是函数f(x)的导函数,y=f '(x)的图象如右图所示,则y=f(x)的图象最有可能的是( )
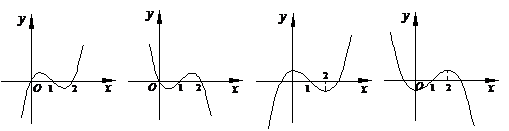
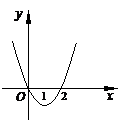
(A) (B) (C) (D)
20.以“时机”为题目,写一篇不少于800字的文章。除诗歌外,文体不限。
13.在横线处写出诗文原句。(8分)
①我欲因之梦吴越, 。湖月照我影, 。
(李白《梦游天姥吟留别》)
②鹤汀凫渚, ;桂殿兰宫, 。
(王勃《滕王阁序》)
③故国神游, ,早生华发。人生如梦, 。
(苏轼《念奴娇·赤壁怀古》)
④醉翁之意不在酒, 。山水之乐, 。
(欧阳修《醉翁亭记》)
12.读下面这首诗,完成①一②题。(7分)
过陈琳①墓
(唐)温庭筠
曾于青史见遗文,今日飘蓬过此坟。
词客有灵应识我,霸才无主始怜君。
石麟埋没藏春草,铜雀②荒凉对暮云。
莫怪临风倍惆怅,欲将书剑学从军。
注:①陈琳:东汉建安七子之一。曾为袁绍起草讨伐曹操的檄文,袁绍败亡后,归附曹操。操不计前赚,予以重用。②铜雀:指曹操修建的铜雀台。
①下列对诗中语句的理解,不正确的一项是(3分) ( )
A.这是一首咏怀古迹的佳作,全诗采用了对比、虚实结合等表现手法,寄托遥深。
B.首联写作者漂泊在外,来到陈琳墓前,无限感慨,表达了他对陈琳的仰慕之情。
C.颈联通过写铜雀台的荒芜寂寥,暗示汉代不重视人才,表现作者对社会的不满。
D.尾联写作者不愿继续临风惆怅,想弃文就武,进一步表现诗人生不逢时之感。
②纪晓岚评颔联中“‘应’字极兀傲(高傲)”。你同意他的说法吗?请结合诗句谈谈你的看法。(4分)
11.用斜线(/)给下面文言文划线的部分断句(5分)
鱼 得 水 而 游 焉 则 乐 塘 决 水 涸 则 为
蝼 蚁 所 食 掌 修 其 堤 防 补 其
缺 漏 则 鱼 得 而 利 之 国 有 以 存 人 有 以 生 国 之 所 以 存 者 仁
蚁 所 食 掌 修 其 堤 防 补 其
缺 漏 则 鱼 得 而 利 之 国 有 以 存 人 有 以 生 国 之 所 以 存 者 仁
义 是 也 人 之 所 以 生 者 行 善 是 也。国无义,虽大必亡;人无善志,虽勇必伤。
(取材于《淮南子》)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com