
21.设二次方程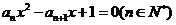 有两个实根
有两个实根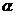 和
和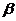 ,
,
且满足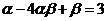 ,
,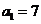 .
.
(1)试用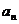 表示
表示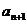 ;
;
(2)求证: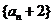 是等比数列;
是等比数列;
(3)求数列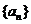 的通项公式.
的通项公式.
20.解:(1)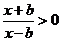 ,即
,即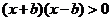 ,而
,而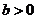 ,
,
得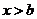 ,或
,或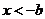 ,
,
即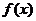 的定义域
的定义域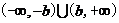 ;
;
(2)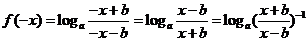 ,
,
即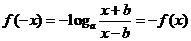 ,
,
得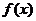 为奇函数;
为奇函数;
(3)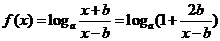 ,
,
令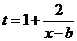 ,在
,在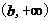 上,
上,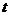 是减函数,
是减函数,
当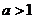 时,
时,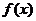 在
在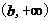 上是减函数,
上是减函数,
当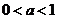 时,
时,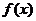 在
在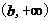 上是增函数;
上是增函数;
(4)令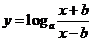 ,得
,得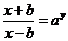 ,
,
即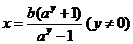 ,
,
得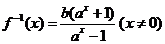 .
.
20.(课本题)已知函数
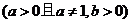 .
.
(1)求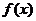 的定义域;
的定义域;
(2)讨论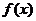 的奇偶性;
的奇偶性;
(3)讨论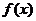 在
在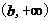 上的单调性;
上的单调性;
(4)求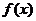 的反函数
的反函数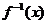 .
.
20.解:(1)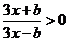 ,即
,即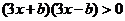 ,而
,而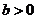 ,
,
得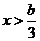 ,或
,或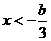 ,
,
即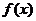 的定义域
的定义域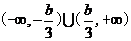 ;
;
(2)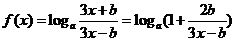 ,
,
令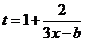 ,在
,在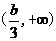 上,
上,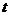 是减函数,
是减函数,
当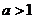 时,
时,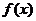 在
在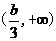 上是减函数,
上是减函数,
当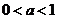 时,
时,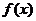 在
在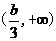 上是增函数.
上是增函数.
20.已知函数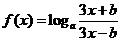
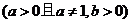 .
.
(1)求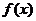 的定义域;
的定义域;
(2)讨论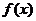 在
在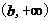 上的单调性.
上的单调性.
19.解: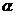 是锐角,
是锐角,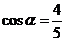 ,得
,得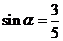 ,
,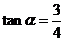 ,
,
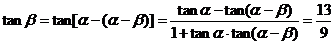 ,
,
得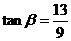 .
.
19.(课本题)已知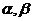 是锐角,
是锐角,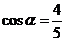 ,
,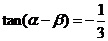 ,求
,求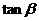 的值.
的值.
19.解:显然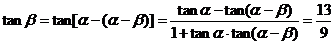 ,
,
而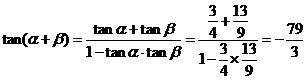 ,
,
即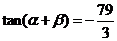 .
.
19.已知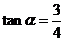 ,
,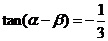 ,求
,求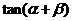 的值.
的值.
18.B 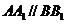 ,过
,过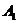 点作平面
点作平面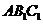 的垂直线,则垂足在等腰三角形
的垂直线,则垂足在等腰三角形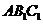 的中线
的中线
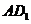 上,连接得
上,连接得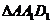 是等腰直角三角形,即
是等腰直角三角形,即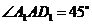 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com