在高中阶阶段学习单调性时，必须让学生对二次函数y=ax²+bx+c在区间(－∞，－]及[－，+∞) 上的单调性的结论用定义进行严格的论证，使它建立在严密理论的基础上，与此同时，进一步充分利用函数图象的直观性，给学生配以适当的练习，使学生逐步自觉地利用图象学习二次函数有关的一些函数单调性。

类型Ⅲ：画出下列函数的图象，并通过图象研究其单调性。

(1)y=x²+2|x－1|－1 (2)y=|x²－1| (3)= x²+2|x|－1

这里要使学生注意这些函数与二次函数的差异和联系。掌握把含有绝对值记号的函数用分段函数去表示，然后画出其图象。

类型Ⅳ设ƒ(x)=x²－2x－1在区间[t,t+1]上的最小值是g(t)。

求：g(t)并画出 y=g(t)的图象

解：ƒ(x)=x²－2x－1=(x－1)²－2，在x=1时取最小值－2

当1∈[t,t+1]即0≤t≤1，g(t)=－2

当t＞1时，g(t)=ƒ(t)=t²－2t－1

当t＜0时，g(t)=ƒ(t+1)=t²－2

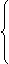　　　　 　　t²－2, (t<0)

　 g(t)= 　-2，(0≤t≤1)

　　　　　 t²－2t－1, (t>1)

首先要使学生弄清楚题意，一般地，一个二次函数在实数集合R上或是只有最小值或是只有最大值，但当定义域发生变化时，取最大或最小值的情况也随之变化，为了巩固和熟悉这方面知识，可以再给学生补充一些练习。

如：y=3x²－5x+6(-3≤x≤－1)，求该函数的值域。

初中阶段已经讲述了函数的定义，进入高中后在学习集合的基础上又学习了映射，接着重新学习函数概念，主要是用映射观点来阐明函数，这时就可以用学生已经有一定了解的函数，特别是二次函数为例来加以更深认识函数的概念。二次函数是从一个集合A(定义域)到集合B(值域)上的映射ƒ:A→B，使得集合B中的元素y=ax²+bx+c(a≠0)与集合A的元素X对应，记为ƒ(x)= ax²+ bx+c(a≠0)这里ax²+bx+c表示对应法则，又表示定义域中的元素X在值域中的象，从而使学生对函数的概念有一个较明确的认识，在学生掌握函数值的记号后，可以让学生进一步处理如下问题：

类型I：已知ƒ(x)= 2x²+x+2，求ƒ(x+1)

这里不能把ƒ(x+1)理解为x=x+1时的函数值，只能理解为自变量为x+1的函数值。

类型Ⅱ：设ƒ(x+1)=x²－4x+1,求ƒ(x)

这个问题理解为，已知对应法则ƒ下，定义域中的元素x+1的象是x²－4x+1，求定义域中元素X的象，其本质是求对应法则。

一般有两种方法：

(1)把所给表达式表示成x+1的多项式。

ƒ(x+1)=x²－4x+1=(x+1)²－6(x+1)+6，再用x代x+1得ƒ(x)=x²－6x+6

(2) 变量代换：它的适应性强，对一般函数都可适用。

　　 令t=x+1，则x=t-1　 ∴(t)=(t-1)²－4(t-1)+1=t²－6t+6从而ƒ(x)= x²－6x+6

建构主义所主张的教学方法与传统的注入式和题海战术，有着本质的区别．建构主义主张的教学方法其核心是强调学习者是一个主动的、积极的知识构造者．他们认为知识就是某观念(belief)；学习是发展，是改变观念；教学是帮助他人发展或改变观念；而行为是人类的活动，其实质是观念的操作化．建构主义认为教师的一项重要的工作就是要从学生实际出发，以深入了解学生真实的思维活动为基础，通过提供适当的问题情景或实例促使学生的反思，引起学生必要的认知冲突，从而让学生最终通过其主动的建构起新的认知结构．传统教学中的注入式和题海战术往往容易忽略学习需要主体的建构，而是把教学最大限度地转移到记忆、复现、再认上去．例如，注入式取消了结论所产生的建构过程，把学习变成反复再现由课本或教师规定的结论；题海战术取消了方法的建构过程，把学习变为重复某些规定的题型解法，等等．传统数学教学的一个主要弊端在于忽视学习者的主观能动性，忽视学习者是学习过程的主体．教师成了知识的“贩卖者”，学生被看成可以任意地涂上各种颜色的白纸，或可以任意地装进各种东西的容器．

建构主义的数学教学观同我国数学教育家积极倡导的“让学生通过自己思维来学习数学”内在本质是一致的．在一定意义上说，我们认为没有一个教师能够教数学，好的教师不是在教数学而是能激发学生自己去学数学．好的教学也并非是把数学内容解释清楚，阐述明白就足够了．事实上，我们往往会发现在教室里除了自己以外，学生并未学懂数学．教师必须要让学生自己研究数学，或者和学生们一起做数学；教师应鼓励学生们独立思考，并接受每个学生做数学的不同想法；教师应积极为学生创设问题解决的情景，让学生通过观察、试验、归纳、作出猜想、发现模式、得出结论并证明、推广，等等．只有当学生通过自己的思考建构起自己的数学理解力时，才能真正学好数学．例如教师在讲授勾股定理时，让学生通过对图形的割、补、拼、凑，学生经过了亲自观察和动手操作，发现了直角三角形三边之间的数量关系．这样不仅使学生认识了勾股定理，熟悉了用面积割补法证明勾股定理的思想，而且更重要的是培养了学生的数学思维能力和自我探究的习惯，激发了学生学习数学的兴趣．

建构主义认为：人的认识本质是主体的“构造”过程．所有的知识都是我们自己的认识活动的结果．我们通过自己的经验来构造自己的理解，反之，我们的经验又受到自己认知“透视”的影响．

数学认识应当被看成是主客体相互作用的产物，也即是反映和建构的辩证统一．如果完全否认了独立于思维的客观世界的存在，并认为认识活动的最终目的不应被看成对于客观真理的追求，则必然导致“极端建构主义”．

在实际数学教学中，我们常常会发现这样的现象，教师总是一个劲的抱怨学生连课堂上讲过的一模一样的习题，在考试中出现时仍然做不出来．这里可以依据建构主义观点作如下的分析：建构主义认为学生学习活动的本质是：学习不应看成对于教师所授予的知识的被动接受，而是一个以学生已有的知识和经验为基础的、社会的建构过程．我们对学生“理解”或“消化”数学知识的真正涵义获得了新的解释，“理解”并不是指学生弄清教师的本意，而是指学习者已有的知识和经验对教师所讲的内容重新加以解释、重新建构其意义，它只是表明学生认为自己“我通过了”．因此，我们不难理解学生所学到的往往并非是教师所教的--这一“残酷”事实．例如在数学教学中最常见的表现是：教师尽管在课堂上讲解得头头是道，学生对此却充耳不闻；教师在课堂上详细分析过的数学习题，学生在作业或测验中仍然可能是谬误百出；教师尽管如何地强调数学的意义，学生却仍然认为数学是毫无意义的符号游戏，等等．学生真正获得对知识的“消化”，是把新的学习内容正确地纳入已有的认知结构，从而使其成为整个结构的有机组成部分．我国著名特级数学教师马明先生有一句很生动的比喻：教师把知识“抛”得越快，学生忘得越快．教得多并不意味着学得也多，有时教得少反而学得多．究其原因，是学生缺乏对数学知识的主动的建构过程．

关于数学学习的建构主义观点是对于传统的数学教育思想，特别是“授予与接受”的观点的直接否定．学习并非一个被动的吸收过程．而是一个以已有知识和经验为基础的主动的建构过程．因此，学习数学的最好方法是做数学，即我们应让学生通过最能展现其建构知识过程的问题解决来学习数学．

早在50-60年代，著名的日内瓦学派创始人、认知心理学家皮亚杰(J．Piaget)曾明确地提出了人的认识并不是对外在的被动的、简单的反映，而是一种以已有知识和经验为基础的主动建构活动的观点(认识的建构主义观点)．由于长期在心理学领域占据主导地位的行为主义学派的巨大影响，使得建构主义观点在很长时期内未得到应有的重视．直到80年代以后随着认知心理学研究的不断深入及其逐渐取代了行为主义的主导地位，才获得人们普遍的重视．

皮亚杰的认知理论的焦点是个体从出生到成年的认知发展阶段．他认为认知发展不是一种数量上简单累积的过程，而是认知结构不断重新建构的过程．根据皮亚杰的观点，个体的认知结构是通过同化和顺化而不断发展，以适应新的环境．个体每当遇到新的刺激，总是把对象纳入到已有的认知结构之中(同化)，若获得成功，便得到暂时的平衡．如果已有的认知结构无法容纳新的对象，个体就必须对已有的认知结构进行变化以使其与环境相适应(顺化)，直至达到认识上的新的平衡．同化与顺化之间的平衡过程，即认识上的“适应”是人类思维的本质所在．

2．关于小组合作学习。

小组合作学习(简称小组合作)是研究性学习的基本组织形式和主要活动方式。研究性学习能否达成预期目标，在很大程度上取决于小组合作的成效如何。小组合作在研究性学习中的意义与传统的以知识为本位的学科教学不同，研究性学习追求多元化的教育价值，小组合作恰好为研究性学习多元化教育价值的实现提供了适当的方式和途径。由于小组是自由组合的，所以小组同学之间互教互学、彼此之间交流都比较顺利，而且使学生能体验到一种被他人接受、信任和认同的情感，有利于提高学生的自信心。当然由于是课堂教学，这种小组合作学习还不是广泛意义上的小组合作，还需要由教师统一规定时间，在课堂内进行。

1．　　　　　　 关于研究性学习。

　　 研究性学习是指学生在教师指导下，从自然、社会和生活中选择和确定专题进行研究，并在研究过程中主动地获取知识、应用知识、解决问题的学习活动。研究性学习强调"体验"这一心理过程，所以我让学生自己选择定理去证明，让学生在实践中去体验和感受发现问题、解决问题的愉悦。 虽然本节课的背景是由我给出的，但是基于部分学生感兴趣的内容而且在自己独立探究的，所以学生还是能发挥自己的学习的主动性，去进行研究性学习。不足之处是由于课堂教学的局限性，不能充分展示每一位学生的研究成果，我认为可以通过班级的学习园地、黑板报等进行展示，从而让更多的学生体验成功的喜悦，提高学习数学的兴趣。

5、薛治刚《高中数学应用问题》吉林科学技术出版社，北京朗曼教学与研究中心1998年11月第1版。

4、黄立俊、方水清《增强应用意识，增强建模能力》中学数学杂志1998年第5期。

3、胡炯涛、张凡编著《中学数学教学纵横谈》山东教育出版社，1997年12月第1版。