
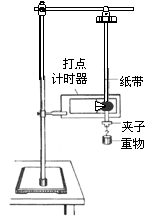
11.(9分)用如图所示的实验装置验证机械能守恒定律.实验所用的电源为学生电源,能输出电压为6V的交流电和直流电.重锤从高处由静止开始下落,打点计时器在重锤拖着的纸带上打出一系列的点,对纸带上某些点的点间距离进行测量,即可验证机械能守恒定律.
(1)下面列举了该实验的几个操作步骤:
A.按照图示的装置安装器件;
B.将打点计时器接到电源的“直流输出”上;
C.用天平测出重锤的质量;
D.先释放悬挂纸带的夹子,后接通电源开关,打出一条纸带;
E.测量纸带上某些点的点间距离;
F.根据测量的结果,计算重锤下落过程中重力势能的减少量是否等于动能的增加量.
没有必要或者操作不当的步骤是 .(填选项对应的字母)
(2)在上述验证机械能守恒定律的实验中发现:
重锤重力势能的减小量总是 (填“大于”、“小于”、或“等于”)重锤动能的增加量,其原因主要是
.
10.如图,把一个带电量为q,质量为m 的小球,用长为L 的绝缘细线悬挂在水平向左的匀强电场中的O点.现将小球拉到B点(悬线拉伸竖直),然后由静止释放,小球恰能摆到A点(悬线拉伸水平),小球摆到C点时,∠BOC=450,则下列说法正确的是
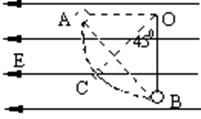 A.匀强电场的场强为mg/q
A.匀强电场的场强为mg/q
B.小球在B点时电势能最小
C.小球在A点时机械能最大
D.小球在C点时动能最大
第Ⅱ卷(非选择题 52分)
 二、实验题(本题共2个题,共18分)
二、实验题(本题共2个题,共18分)
9.在如图所示的电路中,电源电动势为E,内阻为r.闭合开关S,在滑动变阻器的滑片向上滑动过程中,电流表和电压表的示数变化情况为
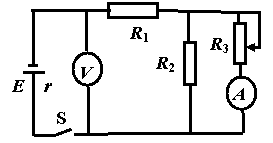 A.电流表和电压表的示数都增大
A.电流表和电压表的示数都增大
B.电流表和电压表的示数都减小
C.电压表的示数增大,电流表的示数减小
D.电压表的示数减小,电流表的示数增大
8.关于超重、失重现象的描述,下列说法正确的是
A.荡秋千时,当秋千摆到最低位置时,人处于失重状态
B.列车在水平直轨道上加速行驶,车上的人处于超重状态
C.在国际空间站内的宇航员处于完全失重状态,因为宇航员不受重力作用
D.电梯减速下降时,电梯中的人处于超重状态
7.已知地球同步卫星的轨道半径约为地球半径的6.6倍,月球绕地球公转的周期约为27.3天,根据以上数据估算地球到月球的距离约为
A.地球半径的40倍 B.地球半径的60倍
C.地球半径的80倍 D.地球半径的100倍
5.如图所示,实线表示匀强电场的电场线.一个带正电荷的粒子以某一速度射入匀强电场,只在电场力作用下,运动的轨迹如图中的虚线所示,a、b为轨迹上的两点.则下列说法正确的是
 A. 场强方向一定向左
A. 场强方向一定向左
B. a点电势比b点电势高
C. 从a到b电场力做负功
D. 该电荷在a点的电势能小于在b点的电势能
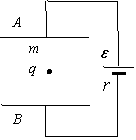 6.如图,平行板电容器的上下极板A、B分别和电池的正极、负极相连,在电容器两极板之间形成的匀强电场中,有一个质量为m、带电量为q的带电粒子始终处于静止状态.若电源的电动势为ε、内阻为r,则下列说法正确的是
6.如图,平行板电容器的上下极板A、B分别和电池的正极、负极相连,在电容器两极板之间形成的匀强电场中,有一个质量为m、带电量为q的带电粒子始终处于静止状态.若电源的电动势为ε、内阻为r,则下列说法正确的是
A. 粒子一定带负电
B. 粒子一定带正电
C. 匀强电场的电场强度为mg/q
D. 极板间的距离为qε/m
4.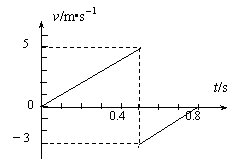 小球从空中某高度处自由下落,与水平地面相碰后(不计碰撞时间)弹到空中某一高度.已知,小球的v-t图象如右图所示,则下列说法中正确的是
小球从空中某高度处自由下落,与水平地面相碰后(不计碰撞时间)弹到空中某一高度.已知,小球的v-t图象如右图所示,则下列说法中正确的是
A.0.3秒末小球下落的速度为4 m/s
B.小球第一次触地后反弹的初速度的大小为-3m/s
C.小球能弹起的最大高度为 1.25m
D.小球能弹起的最大高度为0.45 m
3.下列说法正确的是
A.由R=ρL/s可知:导体电阻与导体的长度成正比,与导体的横截面积成反比
B.由E=F/q可知:电场强度与检验电荷受到的电场力成正比,与检验电荷的电量成反比
C.由F=GmM/r2可知:在国际单位制中,只要公式中各物理量的数值选取恰当,就可使常数G的值为1
D.由F=kq1q2/r2可知:真空中两个点电荷之间的库仑力与两个点电荷电量的乘积成正比,与它们之间距离的平方成反比
1.质点在x轴上运动,初速度v0>0,加速度a>0.在加速度从a逐渐减小到零的过程中,下列说法正确的是
A.速度开始减小,直到加速度等于零为止
B.速度继续增大,直到加速度等于零为止
C.位移先减小后增大,直到加速度等于零为止
D.位移先增大后减小,直到加速度等于零为止
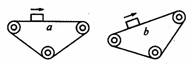 2.在机场和海港,常用输送带运送行李、货物.如图所示,a为水平输送带,b为倾斜输送带.当行李箱随输送带一起匀速运动时,下列几种判断中正确的是
2.在机场和海港,常用输送带运送行李、货物.如图所示,a为水平输送带,b为倾斜输送带.当行李箱随输送带一起匀速运动时,下列几种判断中正确的是
A.a、b两种情形中的行李箱都受到两个力作用
B.a、b两种情形中的行李箱都受到三个力作用
C.情形a中的行李箱受到两个力作用,情形b中的行李箱受到三个力作用
D.情形a中的行李箱受到三个力作用,情形b中的行李箱受到四个力作用
2.3 因为二次函数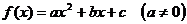 在区间
在区间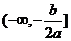 和区间
和区间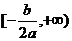 上分别单调,所以函数
上分别单调,所以函数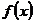 在闭区间上的最大值、最小值必在区间端点或顶点处取得;函数
在闭区间上的最大值、最小值必在区间端点或顶点处取得;函数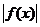 在闭区间上的最大值必在区间端点或顶点处取得.
在闭区间上的最大值必在区间端点或顶点处取得.
例7 已知二次函数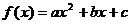 ,当
,当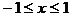 时,有
时,有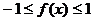 ,求证:当
,求证:当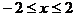 时,有
时,有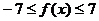 .
.
分析:研究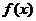 的性质,最好能够得出其解析式,从这个意义上说,应该尽量用已知条件来表达参数
的性质,最好能够得出其解析式,从这个意义上说,应该尽量用已知条件来表达参数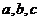 . 确定三个参数,只需三个独立条件,本题可以考虑
. 确定三个参数,只需三个独立条件,本题可以考虑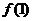 ,
,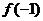 ,
,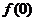 ,这样做的好处有两个:一是
,这样做的好处有两个:一是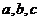 的表达较为简洁,二是由于
的表达较为简洁,二是由于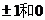 正好是所给条件的区间端点和中点,这样做能够较好地利用条件来达到控制二次函数范围的目的.
正好是所给条件的区间端点和中点,这样做能够较好地利用条件来达到控制二次函数范围的目的.
要考虑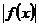 在区间
在区间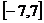 上函数值的取值范围,只需考虑其最大值,也即考虑
上函数值的取值范围,只需考虑其最大值,也即考虑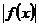 在区间端点和顶点处的函数值.
在区间端点和顶点处的函数值.
解:由题意知: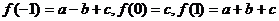 ,
,
∴ 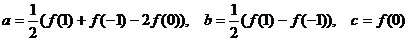 ,
,
∴ 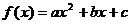
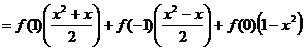 .
.
由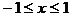 时,有
时,有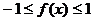 ,可得
,可得 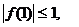
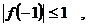
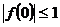 .
.
∴ 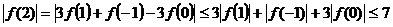 ,
,
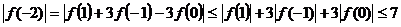 .
.
(1)若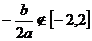 ,则
,则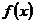 在
在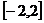 上单调,故当
上单调,故当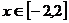 时,
时,
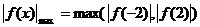
∴ 此时问题获证.
(2)若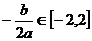 ,则当
,则当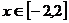 时,
时,
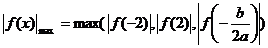
又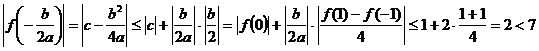 ,
,
∴ 此时问题获证.
综上可知:当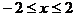 时,有
时,有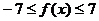 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com