
3.命题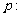 “
“ ”,那么命题
”,那么命题 为
( )
为
( )
A. 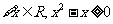 B.
B.
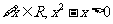
C. 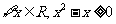 D.
D.
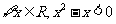
2.已知向量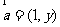 ,
,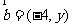 ,且
,且 与
与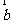 垂直,则
垂直,则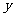 等于( )
等于( )
A.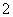 B.
B. .
C.
.
C. .
D.
.
D.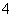
1. 在复平面内,复数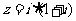 对应的点位于
( )
对应的点位于
( )
A.第一象限 B. 第二象限 C. 第三象限 D. 第四象限
19.(本小题满分14分)
已知椭圆C的中心在坐标原点,离心率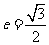 ,一个焦点的坐标为
,一个焦点的坐标为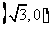 .
.
(I)求椭圆C方程;
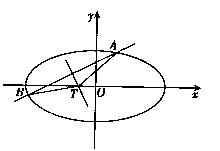 (II)设直线
(II)设直线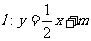 与椭圆C交于A,B两点,线段AB的垂直平分线交
与椭圆C交于A,B两点,线段AB的垂直平分线交 轴于点T.当
轴于点T.当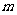 变化
变化
时,求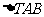 面积的最大值.
面积的最大值.
|
当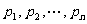 均为正数时,称
均为正数时,称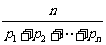 为
为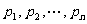 的“均倒数”.已知数列
的“均倒数”.已知数列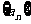 的各项均为正数,且其前
的各项均为正数,且其前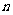 项的“均倒数”为
项的“均倒数”为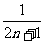 .
.
(Ⅰ)试求数列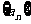 的通项公式;
的通项公式;
(Ⅱ)设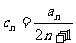 ,试判断并说明
,试判断并说明 的符号;
的符号;
(Ⅲ)已知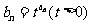 ,记数列
,记数列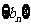 的前
的前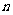 项和为
项和为 ,试求
,试求 的值;
的值;
(Ⅳ)设函数 ,是否存在最大的实数
,是否存在最大的实数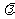 ,使当
,使当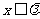 时,对于一切正整数
时,对于一切正整数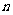 ,
,
都有 恒成立?
恒成立?
怀柔区2009-2010学年度第二学期高三数学期中练习
18.(本小题满分13分)
甲、乙两人同时参加奥运志愿者选拔赛的考试,已知在备选的10道题中,甲能答对其中的6道题,乙能答对其中的8道题.规定每次考试都从备选题中随机抽出3道题进行测试,至少答对2道题才能入选.
(I)求甲答对试题数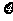 的分布列及数学期望;
的分布列及数学期望;
(II)求甲、乙两人至少有一人入选的概率.
17.(本小题满分13分)
已知函数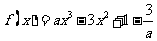
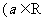 ,且
,且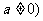 ,求
,求 及函数
及函数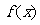 的极大值与极小值.
的极大值与极小值.
16.(本小题满分14分)
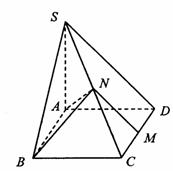 如图,已知四棱锥S-ABCD的底面ABCD是矩形,M、N分别是CD、SC的中点,SA⊥底面ABCD,
如图,已知四棱锥S-ABCD的底面ABCD是矩形,M、N分别是CD、SC的中点,SA⊥底面ABCD,
SA=AD=1,AB=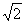 .
.
(I)求证:MN⊥平面ABN;
(II)求二面角A-BN-C的余弦值.
15.(本小题共12分)
已知函数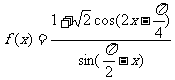 .
.
(Ⅰ)求函数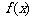 的定义域;
的定义域;
(Ⅱ)求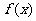 在区间
在区间 上的最大值与最小值.
上的最大值与最小值.
14.已知函数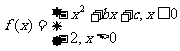 ,若
,若 ,
,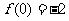 ,则函数
,则函数 的零
的零
点个数为 ____.
13.如图,圆O和圆 相交于A,B两点,AC是圆
相交于A,B两点,AC是圆 的切线,AD是
的切线,AD是
圆O的切线,若BC=2,AB=4,则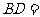 _.
_.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com