
(9)若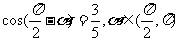 ,则
,则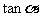 =
.
=
.
(10)如果复数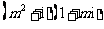 (其中
(其中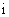 是虚数单位)是实数,则实数
是虚数单位)是实数,则实数
 ___________.
___________.
 (11)从
(11)从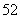 张扑克牌(没有大小王)中随机的抽一张牌,这张牌是
张扑克牌(没有大小王)中随机的抽一张牌,这张牌是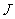 或
或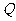 或
或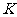 的概率为_______.
的概率为_______.
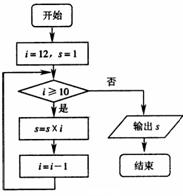
(12)某程序框图如图所示,该程序运行后
输出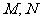 的值分别为 .
的值分别为 .
(13)若数列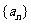 的前
的前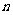 项和为
项和为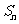 ,则
,则
若数列 的前
的前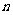 项积为
项积为 ,类比上述结果,则
,类比上述结果,则 =_________;
=_________;
此时,若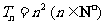 ,则
,则 =___________.
=___________.
(14)关于平面向量有下列四个命题:
①若 ,则
,则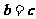 ; ②已知
; ②已知 .若
.若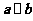 ,则
,则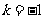 ;
;
③非零向量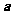 和
和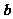 ,满足
,满足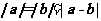 ,则
,则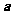 与
与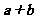 的夹角为
的夹角为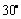 ;
;
④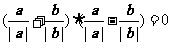 .
.
其中正确的命题为___________.(写出所有正确命题的序号) 三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.
(15)(本小题共12分)
在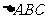 中,角
中,角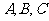 所对的边分别为
所对的边分别为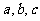 ,满足
,满足 ,且
,且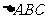 的面积为
的面积为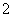 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若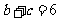 ,求
,求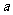 的值.
的值.
(16)(本小题共13分)
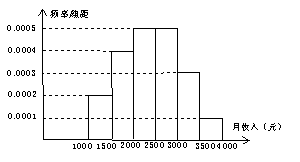
为了调查某厂2000名工人生产某种产品的能力,随机抽查了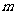 位工人某天生产该产品的数量,产品数量的分组区间为
位工人某天生产该产品的数量,产品数量的分组区间为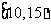 ,
, ,
, ,
,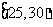 ,
, ,频率分布直方图如图所示.已知生产的产品数量在
,频率分布直方图如图所示.已知生产的产品数量在 之间的工人有6位.
之间的工人有6位.
(Ⅰ)求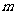 ;
;
(Ⅱ)工厂规定从生产低于20件产品的工人中随机的选取2位工人进行培训,则这2位工
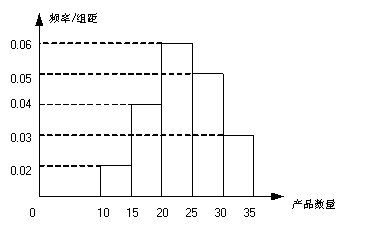 人不在同一组的概率是多少?
人不在同一组的概率是多少?
(17)(本小题共14分)
 三棱柱
三棱柱 中,侧棱与底面垂直,
中,侧棱与底面垂直,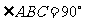 ,
, ,
, 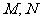 分别是
分别是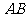 ,
,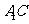 的中点.
的中点.
(Ⅰ)求证: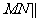 平面
平面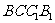 ;
;
(Ⅱ)求证: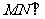 平面
平面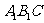 ;
;
(Ⅲ)求三棱锥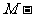
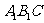 的体积.
的体积.
(18)(本小题共14分)
已知函数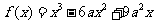 (
(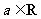 ).
).
(Ⅰ)求函数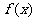 的单调递减区间;
的单调递减区间;
(Ⅱ)当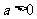 时,若对
时,若对 有
有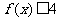 恒成立,求实数
恒成立,求实数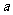 的取值范围.
的取值范围.
(19)(本小题共14分)
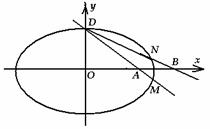 已知椭圆
已知椭圆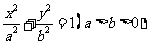 短轴的一个端点
短轴的一个端点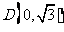 ,离心率
,离心率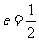 .过
.过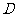 作直线
作直线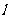 与椭圆交于另一点
与椭圆交于另一点 ,与
,与 轴交于点
轴交于点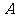 (不同于原点
(不同于原点 ),点
),点 关于
关于 轴的对称点为
轴的对称点为 ,直线
,直线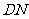 交
交 轴于点
轴于点 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)求
 的值.
的值.
(20)(本小题共13分)
已知数列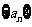 的前
的前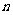 项和为
项和为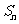 ,且
,且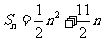 .
.
数列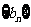 满足
满足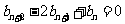 (
(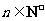 ),且
),且 ,
, .
.
(Ⅰ)求数列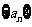 ,
,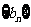 的通项公式;
的通项公式;
(Ⅱ)设 ,数列
,数列 的前
的前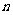 项和为
项和为 ,求使不等式
,求使不等式 对一切
对一切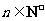 都成立的最大正整数
都成立的最大正整数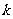 的值;
的值;
(Ⅲ)设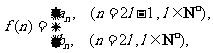 是否存在
是否存在 ,使得
,使得 成立?若存在,求出
成立?若存在,求出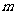 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(考生务必将答案答在答题卡上,在试卷上作答无效)
(1)已知全集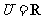 ,集合
,集合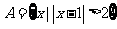 ,
,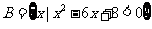 ,则集合
,则集合
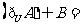
(A)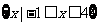 (B)
(B)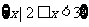
(C) 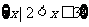 (D)
(D)
(2)已知幂函数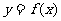 的图象过(4,2)点,则
的图象过(4,2)点,则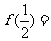
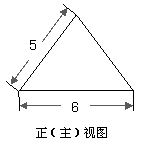 (A)
(A)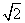 (B)
(B) (C)
(C)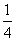 (D)
(D)
 (3)有一个几何体的三视图及其尺寸如图
(3)有一个几何体的三视图及其尺寸如图
(单位: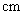 ),该几何体的表面积和体积为
),该几何体的表面积和体积为
(A)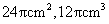
(B)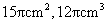
 (C)
(C)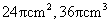
(D)以上都不正确
(4)若直线 与圆
与圆 相切,则
相切,则 的值为
的值为
(A)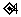 (B)
(B) (C)
(C)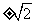 (D)
(D)
(5)将函数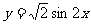 的图象向右平移
的图象向右平移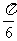 个单位后,其图象的一条对称轴方程为
个单位后,其图象的一条对称轴方程为
(A) 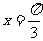 (B)
(B) 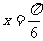 (C)
(C) 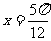 (D)
(D) 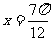
(6)已知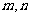 是两条不同直线,
是两条不同直线, 是三个不同平面,下列命题中正确的为
是三个不同平面,下列命题中正确的为
(A)若 则
则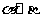 (B)若
(B)若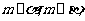 则
则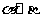
(C)若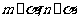 ,则
,则 (D)若
(D)若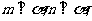 则
则
(7)若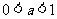 ,函数
,函数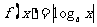 ,
,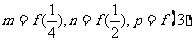 ,则
,则
(A)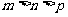 (B)
(B)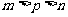 (C)
(C)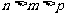 (D)
(D)
(8)如果对于任意实数 ,
,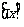 表示不超过
表示不超过 的最大整数. 例如
的最大整数. 例如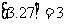 ,
,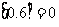 .
.
那么“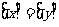 ”是“
”是“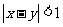 ”的
”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
崇文区2009-2010学年度第二学期统一练习(一)
高三数学(文科) 2010.4
第Ⅱ卷(共110分)
20. (本题满分14分)
已知数列 中,
中, ,
, ,其前
,其前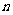 项和
项和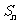 满足
满足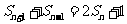 (
(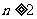 ,
,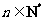 ).
).
(1)求数列 的通项公式;
的通项公式;
(2)设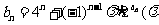 为非零整数,
为非零整数,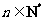 ),试确定
),试确定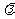 的值,使得对任意
的值,使得对任意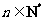 ,都有
,都有 成立.
成立.
19. (本题满分14分)
在直角坐标系xOy中,椭圆C1: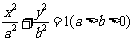 的左、右焦点分别为F1、F2.其中F2也是抛物线C2:
的左、右焦点分别为F1、F2.其中F2也是抛物线C2: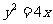 的焦点,点M为C1与C2在第一象限的交点,且
的焦点,点M为C1与C2在第一象限的交点,且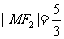 .
.
(1)求C1的方程;
(2)平面上的点N满足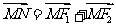 ,直线l∥MN,且与C1交于A、B两点,若
,直线l∥MN,且与C1交于A、B两点,若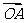 ·
·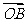 =0,求直线l的方程.
=0,求直线l的方程.
18.(本小题满分14分)
已知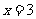 是函数
是函数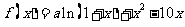 的一个极值点.
的一个极值点.
(Ⅰ)求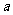 ;
;
(Ⅱ)求函数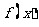 的单调区间;
的单调区间;
(Ⅲ)若直线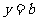 与函数
与函数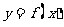 的图象有3个交点,求
的图象有3个交点,求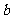 的取值范围.
的取值范围.
17. (本小题满分13分)
甲乙两队参加奥运知识竞赛,每队3人,每人回答一个问题,答对者为本队赢得一分,答错得零分.假设甲队中每人答对的概率均为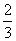 ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为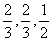 且各人正确与否相互之间没有影响.用ξ表示甲队的总得分.
且各人正确与否相互之间没有影响.用ξ表示甲队的总得分.
(Ⅰ)求随机变量ξ分布列和数学期望;
(Ⅱ)用A表示“甲、乙两个队总得分之和等于3”这一事件,用B表示“甲队总得分大于乙队总得分”这一事件,求P(AB).
15. (本题满分12分)
已知函数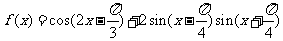
(Ⅰ)求函数 的最小正周期和图象的对称轴方程
的最小正周期和图象的对称轴方程
(Ⅱ)求函数 在区间
在区间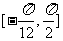 上的值域.
上的值域.
16(本题满分13分)
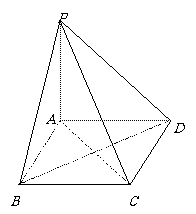
如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD= .
.
(Ⅰ)求证: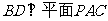 ;
;
(Ⅱ)求二面角 的余弦值;
的余弦值;
 (III)在线段
(III)在线段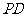 上是否存在一点
上是否存在一点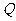 ,使
,使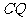 与平面
与平面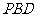 所成的角的正弦值为
所成的角的正弦值为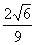 ,若存在,指出点
,若存在,指出点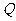 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.
14.给出以下几个命题:
①由曲线y=x2与直线y=2x围成的封闭区域的面积为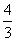 .
.
②已知点A是定圆C上的一个定点,线段AB为圆的动弦,若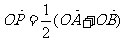 ,
,
O为坐标原点,则动点P的轨迹为圆;
③把5本不同的书分给4个人,每人至少1本,则不同的分法种数为A54·A41=480种.
④若直线l//平面α,直线l⊥直线m,直线
 平面β,则β⊥α,其中,正确的命题有
. (将所有正确命题的序号都填在横线上)
平面β,则β⊥α,其中,正确的命题有
. (将所有正确命题的序号都填在横线上)
13. 在平面直角坐标系xOy 中,直线 的参数方程为
的参数方程为 (参数t∈R),圆C的参数方程为
(参数t∈R),圆C的参数方程为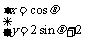 (参数
(参数 ),则圆C的圆心坐标为_______,圆心到直线
),则圆C的圆心坐标为_______,圆心到直线 的距离为______.
的距离为______.
12.右面框图表示的程序所输出的结果是_______ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com