
解得h=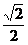 a.即点C到平面PDE的距离为
a.即点C到平面PDE的距离为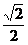 a. 16分
a. 16分
即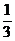 a3=
a3=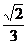 a2h,
a2h,
则V C-PDE=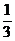 ?h?S△PDE=
?h?S△PDE=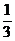 ?h?
?h?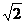 a2=
a2=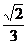 a2h.
a2h.
∵VP-CDE=VC-PDE,
∵VP-CDE=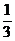 ?PA?S△CDE=
?PA?S△CDE=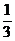 ?2a?
?2a?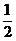 a2=
a2=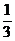 a2. 13分
a2. 13分
设点C到平面PDE的距离为h,
则S△CDE=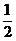 a2,S△DEP=
a2,S△DEP=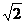 a2 .
a2 .
 ∴FG=
∴FG=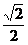 a. ∴点C到平面PDE的距离为
a. ∴点C到平面PDE的距离为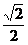 a. 16分
a. 16分
解法二:∵PA平面ABCDE,∴PA⊥DE,
又∵∠DEA=90°,∴DE⊥平面PAE,∴DE⊥PE.
∵BC=DE=a,AB=AE=2a,
连接CE,
∴CF∥DE,而DE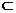 平面PDE,CF
平面PDE,CF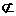 平面PDE,
平面PDE,
∴CF∥平面PDE.
∴点C到平面PDE的距离等于F到平面PDE的距离.
∵PA⊥平面ABCDE,
∴PA⊥DE.
又∵DE⊥AE,∴DE⊥平面PAE.
∴平面PAE⊥平面PDE.∴过F作FG⊥PE于G,则FG⊥平面PDE.
∴FG的长即F点到平面PDE的距离. 13分
在△PAE中,PA=AE=2a,F为AE中点,FG⊥PE,
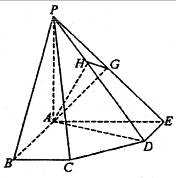 (3)解法一:∵∠EAB=∠ABC=∠DEA=90°,
(3)解法一:∵∠EAB=∠ABC=∠DEA=90°,
BC=DE=a,AB=AE=2a,
取AE中点F,连CF,
∵AF∥=BC,
∴四边形ABCF为平行四边形.
∴CF∥AB,而AB∥DE,
∴二面角A-PD-E的大小为arccos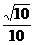 . 10分
. 10分
∴<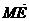 ,
,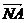 >=arccos=
>=arccos=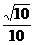 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com